6 8 As A Percent
marihuanalabs
Sep 24, 2025 · 5 min read
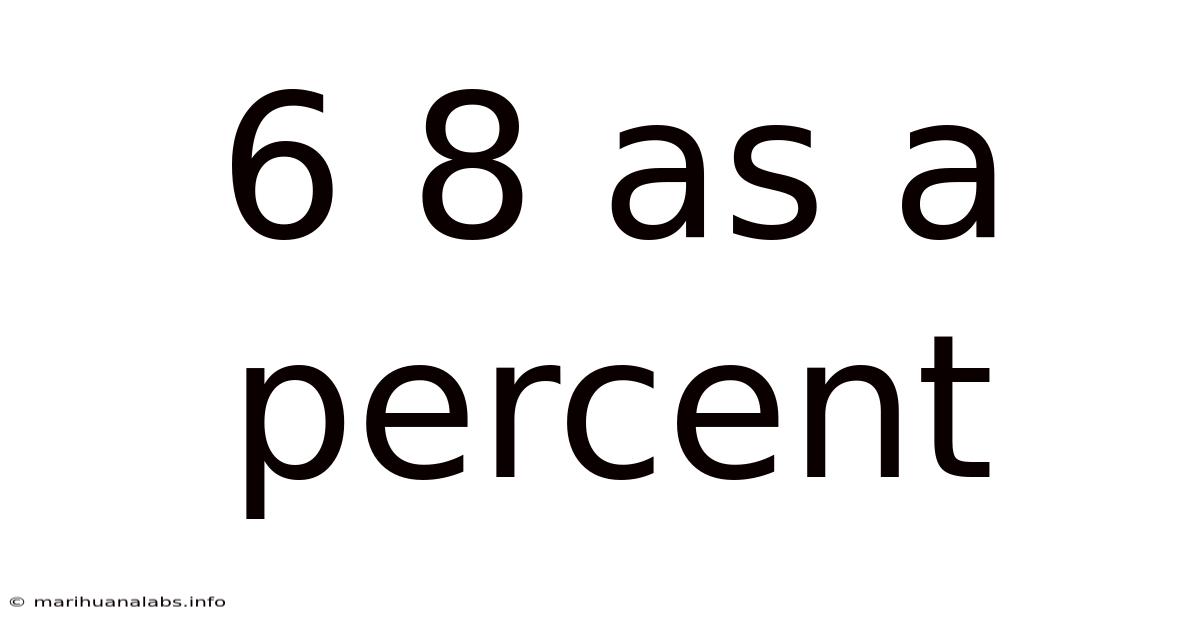
Table of Contents
Understanding 6/8 as a Percentage: A Comprehensive Guide
What does 6/8 as a percent actually mean? This seemingly simple question opens the door to a deeper understanding of fractions, decimals, and percentages – fundamental concepts in mathematics with applications across countless fields. This article will not only show you how to calculate 6/8 as a percentage but also explore the underlying principles, provide practical examples, and answer frequently asked questions. We'll delve into the methods, explaining each step clearly so you can confidently tackle similar problems in the future.
Understanding Fractions, Decimals, and Percentages
Before we dive into calculating 6/8 as a percentage, let's refresh our understanding of these three interconnected concepts:
-
Fractions: A fraction represents a part of a whole. It's expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). In our case, 6/8 means 6 parts out of a total of 8 parts.
-
Decimals: Decimals are another way to represent parts of a whole. They use a base-ten system, with the digits to the right of the decimal point representing tenths, hundredths, thousandths, and so on.
-
Percentages: Percentages express a fraction or decimal as a proportion of 100. The symbol "%" signifies "per hundred." A percentage is simply a fraction with a denominator of 100.
These three concepts are interchangeable; you can convert between them easily using simple mathematical operations.
Method 1: Simplifying the Fraction Before Conversion
The fraction 6/8 can be simplified before converting it to a percentage. Simplifying a fraction means reducing it to its lowest terms by dividing both the numerator and the denominator by their greatest common divisor (GCD). The GCD of 6 and 8 is 2.
-
Simplify the Fraction: Divide both the numerator (6) and the denominator (8) by 2: 6 ÷ 2 = 3 8 ÷ 2 = 4 This simplifies the fraction to 3/4.
-
Convert the Simplified Fraction to a Decimal: To convert a fraction to a decimal, divide the numerator by the denominator: 3 ÷ 4 = 0.75
-
Convert the Decimal to a Percentage: To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol: 0.75 × 100 = 75%
Therefore, 6/8 is equal to 75%.
Method 2: Direct Conversion from Fraction to Percentage
You can also convert 6/8 directly to a percentage without simplifying the fraction first.
-
Convert the Fraction to a Decimal: Divide the numerator (6) by the denominator (8): 6 ÷ 8 = 0.75
-
Convert the Decimal to a Percentage: Multiply the decimal by 100 and add the "%" symbol: 0.75 × 100 = 75%
Again, we arrive at the answer: 6/8 is equal to 75%.
Illustrative Examples: Real-World Applications
Let's illustrate the practical application of understanding 6/8 as 75% with some real-world scenarios:
-
Test Scores: If a student answered 6 out of 8 questions correctly on a quiz, their score is 75%.
-
Sales: A store offering a 75% discount on an item is essentially offering the item at 6/8 (or 3/4) of its original price.
-
Surveys: If 6 out of 8 respondents in a survey agreed with a particular statement, then 75% of the respondents agreed.
-
Project Completion: If 6 out of 8 tasks in a project are complete, then 75% of the project is finished.
These examples demonstrate how the concept of 6/8 as 75% can be applied to various everyday situations.
Scientific Explanation: Proportions and Ratios
From a scientific perspective, the conversion of 6/8 to 75% involves understanding proportions and ratios. A ratio is a comparison of two quantities, while a proportion is a statement that two ratios are equal. In the context of 6/8, the ratio is 6:8, which can be expressed as the fraction 6/8. To find the percentage, we're essentially finding an equivalent ratio with a denominator of 100. This can be achieved through cross-multiplication or by converting the fraction to a decimal and then multiplying by 100. The underlying principle is the equivalence of ratios, a fundamental concept in various scientific disciplines.
Frequently Asked Questions (FAQ)
Q1: Can I simplify a fraction before converting it to a percentage?
A1: Yes, simplifying a fraction makes the conversion to a percentage easier and often leads to a cleaner answer. It doesn't change the final percentage; it simply streamlines the calculation process.
Q2: What if the fraction doesn't divide evenly?
A2: If the fraction doesn't divide evenly, you'll get a decimal with more digits after the decimal point. You can either round the decimal to a specific number of decimal places before converting to a percentage or leave the percentage in decimal form.
Q3: Is there a formula for converting fractions to percentages?
A3: Yes, the formula is: (Numerator/Denominator) * 100 = Percentage
Q4: Why is understanding percentages important?
A4: Percentages provide a standardized way to compare and understand proportions. They're essential in various fields, including finance, statistics, science, and everyday life. They allow us to easily understand proportions and make informed decisions.
Q5: Are there any online calculators to help with this type of conversion?
A5: Yes, numerous online calculators can help convert fractions to percentages. However, understanding the underlying principles is more valuable than solely relying on calculators.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting 6/8 to a percentage, resulting in 75%, is a straightforward process, but it highlights the fundamental connection between fractions, decimals, and percentages. By understanding the underlying principles and the various methods for conversion, you can confidently tackle similar problems and apply this knowledge to various real-world situations. Remember, the ability to convert between these different representations of portions is a crucial skill in mathematics and numerous other disciplines. Practice makes perfect, so keep working on these conversions to solidify your understanding. You now possess the tools and knowledge to tackle fraction-to-percentage conversions with ease and confidence!
Latest Posts
Latest Posts
-
Born Haber Cycle Of Mgcl2
Sep 24, 2025
-
God Is Omniscient Omnipresent Omnipotent
Sep 24, 2025
-
7 4 As A Decimal
Sep 24, 2025
-
55 Degrees C To F
Sep 24, 2025
-
How Long Is The Pencil
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 6 8 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.