7 4 As A Decimal
marihuanalabs
Sep 24, 2025 · 6 min read
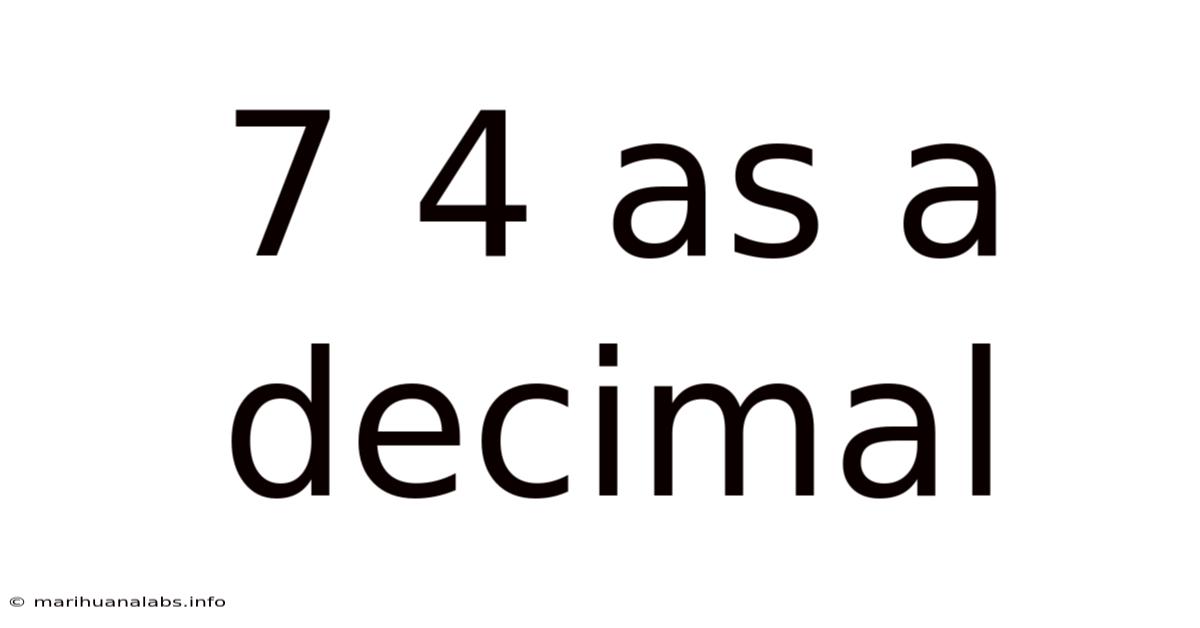
Table of Contents
Decoding 7/4 as a Decimal: A Comprehensive Guide
Understanding fractions and their decimal equivalents is fundamental to mathematics. This comprehensive guide will delve deep into converting the fraction 7/4 into its decimal form, exploring various methods, underlying principles, and practical applications. We’ll move beyond a simple answer and uncover the mathematical concepts that make this conversion possible. Learn how to tackle similar fraction-to-decimal conversions with confidence.
Introduction: Understanding Fractions and Decimals
Before jumping into the conversion of 7/4, let's refresh our understanding of fractions and decimals. A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts we have, while the denominator indicates how many equal parts the whole is divided into.
A decimal, on the other hand, represents a number based on the powers of 10. It uses a decimal point to separate the whole number part from the fractional part. Decimals are a convenient way to express fractions, especially when performing calculations.
Method 1: Long Division
The most straightforward method to convert a fraction to a decimal is through long division. We divide the numerator (7) by the denominator (4).
-
Set up the long division: Write 7 as the dividend (inside the division symbol) and 4 as the divisor (outside the division symbol).
-
Divide: 4 goes into 7 one time (4 x 1 = 4). Write "1" above the 7.
-
Subtract: Subtract 4 from 7, leaving 3.
-
Bring down a zero: Add a decimal point to the quotient (the answer) and bring down a zero to make 30.
-
Continue dividing: 4 goes into 30 seven times (4 x 7 = 28). Write "7" above the zero.
-
Subtract: Subtract 28 from 30, leaving 2.
-
Repeat: Bring down another zero to make 20. 4 goes into 20 five times (4 x 5 = 20). Write "5" above the zero.
-
Subtract: Subtract 20 from 20, leaving 0. The division is complete.
Therefore, 7/4 = 1.75
This method clearly demonstrates the process of converting a fraction to its decimal equivalent. The resulting decimal, 1.75, shows that 7/4 is equivalent to one and three quarters (1 + 3/4).
Method 2: Converting to a Mixed Number
Before employing long division, we can simplify the fraction by converting it into a mixed number. A mixed number combines a whole number and a fraction.
-
Divide the numerator by the denominator: 7 divided by 4 is 1 with a remainder of 3.
-
Express as a mixed number: This means 7/4 can be written as 1 and 3/4 (1 3/4).
-
Convert the fraction part to a decimal: Now, we only need to convert the fractional part, 3/4, to a decimal. Using long division (or recognizing that 3/4 is a common fraction equal to 0.75), we get 0.75.
-
Combine the whole number and the decimal: Add the whole number 1 to the decimal 0.75 to obtain 1.75.
Thus, 7/4 = 1 3/4 = 1.75
This method offers an alternative approach, particularly helpful when dealing with improper fractions (where the numerator is larger than the denominator) as it provides a better understanding of the magnitude of the fraction.
Method 3: Using Decimal Equivalents of Common Fractions
For frequently encountered fractions, memorizing their decimal equivalents can significantly speed up conversions. Knowing that 1/4 = 0.25, we can easily deduce that 3/4 = 0.75 and subsequently that 7/4 = 1 + 3/4 = 1 + 0.75 = 1.75.
This method leverages prior knowledge to efficiently solve the problem, highlighting the importance of learning common fraction-decimal equivalents.
Understanding the Result: 1.75
The decimal 1.75 represents one and seventy-five hundredths. It signifies that the value is greater than 1 and less than 2. Visually, if we imagine a pie chart divided into four equal parts, 7/4 would represent one whole pie plus three additional quarters of another pie. This corresponds perfectly to 1.75.
Practical Applications of Decimal Conversions
Converting fractions to decimals is crucial in various fields:
-
Finance: Calculating interest rates, discounts, and profit margins often requires converting fractions to decimals for ease of computation.
-
Engineering: Precise measurements and calculations in engineering rely heavily on decimal representations.
-
Science: Expressing experimental results, such as measurements of length, weight, or volume, often involves decimals.
-
Everyday Life: Many everyday calculations, like splitting a bill or calculating sale prices, benefit from converting fractions to decimals.
Further Exploration: Converting Other Fractions
The techniques used to convert 7/4 to a decimal can be applied to other fractions. Remember to:
- Identify the numerator and denominator.
- Use long division or convert to a mixed number first.
- Utilize known decimal equivalents of common fractions whenever possible.
- Practice regularly to build proficiency.
For example, let’s convert 5/8:
Using long division: 5 ÷ 8 = 0.625
Or, we can understand that 1/8 = 0.125, therefore 5/8 = 5 x 0.125 = 0.625.
Frequently Asked Questions (FAQ)
Q1: What if the decimal representation of a fraction is non-terminating?
Some fractions, when converted to decimals, result in non-terminating decimals (decimals that go on forever). For example, 1/3 = 0.3333... In such cases, we can round off the decimal to a certain number of decimal places depending on the required accuracy.
Q2: Is there a quicker way to convert fractions to decimals besides long division?
For simple fractions, recognizing their equivalent decimal values or converting to a mixed number and then converting the fractional part can be quicker. Calculators are also very helpful tools.
Q3: Can negative fractions be converted to decimals?
Yes, the process remains the same. Convert the absolute value of the fraction to a decimal and then add the negative sign. For example, -7/4 = -1.75.
Q4: Why is understanding fraction-to-decimal conversion important?
It's fundamental for many mathematical operations and crucial for applications in various fields, including finance, engineering, and science. It bridges the gap between different representations of numbers, making calculations more efficient.
Conclusion: Mastering Fraction-to-Decimal Conversions
Converting 7/4 to its decimal equivalent, 1.75, highlights the importance of understanding the relationship between fractions and decimals. Through long division, converting to mixed numbers, or utilizing known decimal equivalents of common fractions, we can successfully perform this conversion. This knowledge empowers us to confidently tackle similar problems and apply these principles in various practical contexts. Remember that consistent practice is key to mastering this essential mathematical skill. The ability to seamlessly switch between fraction and decimal representations expands our mathematical fluency and opens doors to a deeper understanding of numerical concepts.
Latest Posts
Latest Posts
-
Borges And Me Film 2024
Sep 24, 2025
-
How To Draw Regular Pentagon
Sep 24, 2025
-
When Is The 16th Century
Sep 24, 2025
-
A Good Walk Spoiled Quote
Sep 24, 2025
-
Definition Of Specialisation In Economics
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about 7 4 As A Decimal . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.