X 2 X 2 Y
marihuanalabs
Sep 12, 2025 · 5 min read
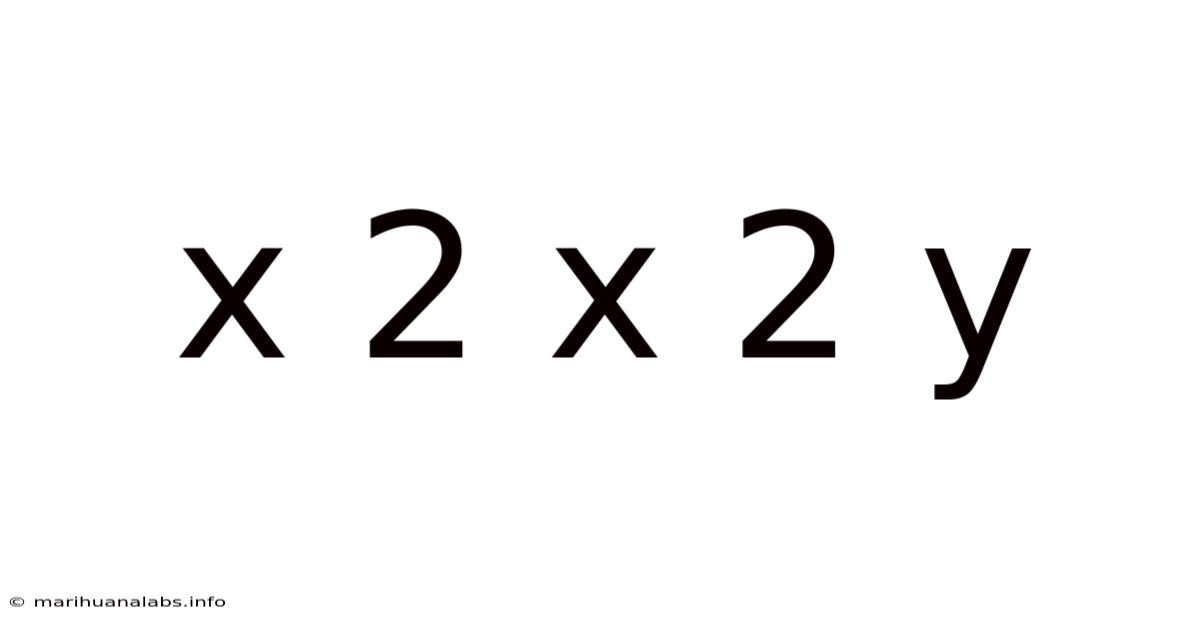
Table of Contents
Decoding the Mystery: A Deep Dive into x² x²y
The expression "x² x²y" might seem deceptively simple at first glance. However, a deeper understanding reveals its multifaceted nature and its significance across various mathematical disciplines. This article aims to demystify this expression, exploring its simplification, applications, and underlying mathematical concepts. We will examine its algebraic manipulation, geometrical interpretations, and potential connections to calculus and other advanced areas. By the end, you'll not only understand how to simplify x² x²y but also appreciate its broader mathematical context.
Understanding the Fundamentals: Algebraic Simplification
At its core, "x² x²y" represents a product of algebraic terms. Let's break it down step-by-step. The expression consists of:
- x²: This represents 'x' multiplied by itself (x * x). It's a term with a base of 'x' and an exponent of 2.
- x²: Identical to the first term, this again represents x * x.
- y: This is a single variable, representing an unknown quantity.
To simplify the expression, we utilize the commutative and associative properties of multiplication. These properties state that the order in which we multiply numbers or variables doesn't affect the result. Therefore, we can rearrange and group the terms:
x² x² y = (x² * x²) * y
Now, let's simplify the product of the x² terms:
x² * x² = x^(2+2) = x⁴
This simplification uses the rule of exponents for multiplication: when multiplying terms with the same base, add the exponents. Therefore, our simplified expression becomes:
x⁴y
This is the most concise and simplified form of the original expression. It represents 'x' raised to the power of 4, multiplied by 'y'.
Visualizing the Concept: Geometrical Interpretations
While the algebraic simplification is straightforward, understanding the geometrical interpretation can provide valuable insight. Let's consider scenarios where this expression might arise:
Scenario 1: Area of a Rectangle
Imagine a rectangle with sides of length x² and x²y. The area of a rectangle is calculated by multiplying its length and width. In this case, the area would be:
Area = x² * x²y = x⁴y
This visualization demonstrates that x⁴y represents the area of a rectangle with sides of length x² and x²y. The dimensions themselves represent areas of squares and rectangles, further highlighting the power of this expression.
Scenario 2: Volume of a Rectangular Prism
Expanding on the previous scenario, consider a rectangular prism (a three-dimensional box). Let's say the dimensions are x², x², and y. The volume of a rectangular prism is calculated by multiplying its length, width, and height. Therefore, the volume would be:
Volume = x² * x² * y = x⁴y
This shows that x⁴y can also represent the volume of a specific three-dimensional shape. These geometric examples demonstrate the practical applications of the expression beyond abstract algebraic manipulation.
Beyond Simplification: Exploring Advanced Applications
The expression x⁴y, though seemingly basic, serves as a building block for more complex mathematical concepts. Its application extends beyond elementary algebra to more advanced fields:
1. Calculus: In calculus, expressions like x⁴y can represent functions of multiple variables. These functions can then be used to model various phenomena, including:
- Optimization Problems: Finding maximum or minimum values of functions.
- Partial Derivatives: Analyzing the rate of change of a function with respect to one variable, while holding others constant.
- Multiple Integrals: Calculating areas and volumes in higher dimensions.
2. Linear Algebra: The expression can be seen within the context of vectors and matrices. Consider a vector with components involving x⁴y. Matrix multiplication involving such vectors would lead to more complex expressions, but x⁴y would still form a fundamental component.
3. Differential Equations: Differential equations involve equations with derivatives. Solving these equations often requires manipulating expressions like x⁴y. For example, finding a solution that satisfies a specific differential equation might involve expressing the solution in terms of x⁴y.
Addressing Common Queries: FAQs
Q1: Can x and y be negative numbers?
A1: Yes, x and y can be negative numbers. However, remember that the exponent only affects the base. For example, if x = -2, then x⁴ = (-2)⁴ = 16 (a positive number). The overall sign of x⁴y will depend on the signs of x and y. If both are negative, the result will be positive; if one is negative and the other positive, the result will be negative.
Q2: What if the expression were (x²) (x²y)?
A2: This is the same as x² x²y. The parentheses simply show the grouping of the terms. The simplification remains the same: x⁴y.
Q3: What happens if y=0?
A3: If y = 0, the entire expression becomes 0. This is because anything multiplied by zero is zero. Therefore, x⁴ * 0 = 0.
Q4: How does this relate to polynomial functions?
A4: The simplified expression x⁴y is a term within a polynomial if it's combined with other terms of the form axⁿyᵐ, where 'a' is a constant and 'n' and 'm' are non-negative integers. Polynomials are fundamental in many areas of mathematics.
Q5: Can this expression be factored further?
A5: The simplified form x⁴y can be factored to some extent, depending on the context. For instance, it could be factored as x³(xy) or x²(x²y). However, without additional information or constraints, these factorizations aren't typically more useful than the simplified form.
Conclusion: More Than Meets the Eye
The seemingly simple expression "x² x²y" reveals a depth of mathematical concepts. From its straightforward algebraic simplification to its geometrical interpretations and applications in advanced areas like calculus and linear algebra, this expression highlights the interconnectedness of various mathematical disciplines. Understanding the simplification, x⁴y, is crucial not only for basic algebra but also for building a foundation in more advanced areas. Remember that each mathematical concept builds upon the previous ones; understanding the simpler expressions helps you tackle the more complex ones. This deep dive hopefully demystified the expression and inspired further exploration into the fascinating world of mathematics.
Latest Posts
Latest Posts
-
How Is Halal Food Prepared
Sep 12, 2025
-
6 25 As A Percent
Sep 12, 2025
-
Driving And Realistic Personality Meaning
Sep 12, 2025
-
Math In The Real World
Sep 12, 2025
-
How Many Inches Is 50cm
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about X 2 X 2 Y . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.