6 25 As A Percent
marihuanalabs
Sep 12, 2025 · 5 min read
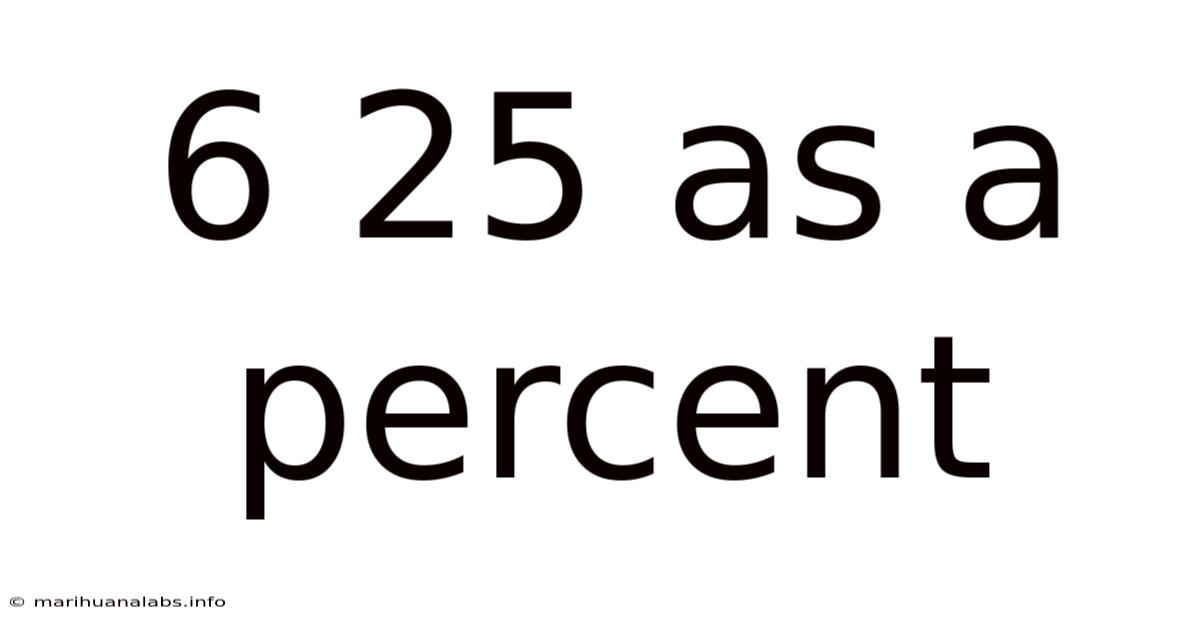
Table of Contents
6/25 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with wide-ranging applications in everyday life, from calculating discounts and tips to understanding statistics and financial data. This comprehensive guide will delve into the process of converting the fraction 6/25 into a percentage, explaining the method step-by-step and exploring the underlying concepts. We'll also look at different approaches and address frequently asked questions to solidify your understanding. By the end, you'll not only know the answer but also possess a deeper understanding of percentage calculations.
Understanding Fractions and Percentages
Before diving into the conversion, let's briefly review the concepts of fractions and percentages.
A fraction represents a part of a whole. It consists of a numerator (the top number) and a denominator (the bottom number). The numerator indicates how many parts you have, while the denominator indicates how many parts make up the whole. For example, in the fraction 6/25, 6 represents the number of parts and 25 represents the total number of parts that make up the whole.
A percentage is a way of expressing a number as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Percentages are often used to express proportions, rates, or changes. For instance, 25% means 25 out of 100, or 25/100.
Converting 6/25 to a Percentage: The Step-by-Step Method
There are several ways to convert a fraction to a percentage. Here's the most common and straightforward method:
Step 1: Convert the fraction to a decimal.
To convert a fraction to a decimal, you simply divide the numerator by the denominator. In this case:
6 ÷ 25 = 0.24
Step 2: Convert the decimal to a percentage.
To convert a decimal to a percentage, multiply the decimal by 100 and add the "%" symbol.
0.24 x 100 = 24%
Therefore, 6/25 is equal to 24%.
Alternative Methods for Conversion
While the above method is the most common, there are alternative approaches you can use, depending on your preference and the complexity of the fraction:
Method 2: Finding an Equivalent Fraction with a Denominator of 100
This method involves finding an equivalent fraction where the denominator is 100. Since percentages are based on 100, this directly gives you the percentage.
To do this, we need to find a number that, when multiplied by 25, equals 100. That number is 4 (25 x 4 = 100). Whatever we multiply the denominator by, we must also multiply the numerator by the same number to maintain the fraction's value.
So, we multiply both the numerator and denominator of 6/25 by 4:
(6 x 4) / (25 x 4) = 24/100
Since 24/100 means 24 out of 100, this directly translates to 24%.
Method 3: Using Proportions
This method utilizes the concept of proportions. We can set up a proportion to solve for the percentage:
6/25 = x/100
To solve for x (the percentage), we can cross-multiply:
25x = 600
x = 600 ÷ 25
x = 24
Therefore, 6/25 = 24%.
Understanding the Concept: What does 24% actually mean?
Having calculated that 6/25 equals 24%, it's crucial to understand the practical implications. 24% signifies that for every 100 units of a whole, 24 units are represented by the fraction 6/25. Imagine you have a bag of 100 marbles. If 24 of those marbles are red, then the proportion of red marbles can be expressed as 24%, which is equivalent to the fraction 24/100 or the simplified fraction 6/25.
Real-World Applications of Fraction-to-Percentage Conversion
The ability to convert fractions to percentages is essential in various real-world scenarios:
- Calculating Discounts: A store offers a 24% discount on an item. Understanding this percentage helps you determine the actual price reduction.
- Analyzing Financial Data: Financial reports frequently use percentages to represent growth rates, profit margins, and other key indicators.
- Understanding Statistics: Percentages are ubiquitous in statistical analysis, making it easier to interpret data and draw meaningful conclusions.
- Calculating Grades: Many educational systems use percentages to represent student performance on tests and assignments.
- Determining Tax Rates: Tax rates are often expressed as percentages, enabling straightforward calculation of the tax amount.
Frequently Asked Questions (FAQs)
Q1: Can I convert any fraction to a percentage?
A1: Yes, you can convert any fraction to a percentage by following the methods described above. However, the resulting percentage might be a decimal percentage (e.g., 33.33%).
Q2: What if the fraction is an improper fraction (numerator is larger than the denominator)?
A2: You can still convert an improper fraction to a percentage using the same methods. The resulting percentage will be greater than 100%.
Q3: Are there any online tools or calculators to help with this conversion?
A3: Yes, many online calculators and converters can help with fraction-to-percentage conversions. These tools can be particularly helpful for complex fractions or when you need quick results.
Q4: Why is understanding percentage conversion important?
A4: Understanding percentage conversion is crucial for effective communication, problem-solving, and critical thinking. It equips you to interpret data, analyze situations, and make informed decisions in various aspects of life.
Conclusion
Converting fractions to percentages is a fundamental mathematical skill with far-reaching applications. We've explored different methods for converting 6/25 to a percentage, ultimately arriving at the answer: 24%. Understanding these methods, not just the answer, empowers you to confidently tackle similar conversions and apply this skill in various contexts. Remember, the ability to convert between fractions and percentages is a valuable asset, enhancing your numerical fluency and problem-solving capabilities. Practice these methods with different fractions to build your confidence and solidify your understanding. You’ll find that with a little practice, this skill becomes second nature, helping you navigate the numerical world with greater ease and proficiency.
Latest Posts
Latest Posts
-
Effie Trinket Catching Fire Costume
Sep 12, 2025
-
Dogs Name On Neverending Story
Sep 12, 2025
-
Ionic Covalent And Metallic Bonds
Sep 12, 2025
-
Directional And Nondirectional Hypothesis Examples
Sep 12, 2025
-
What Is Rapid Thermal Annealing
Sep 12, 2025
Related Post
Thank you for visiting our website which covers about 6 25 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.