Whats 25 Percent Of 1000
marihuanalabs
Sep 16, 2025 · 4 min read
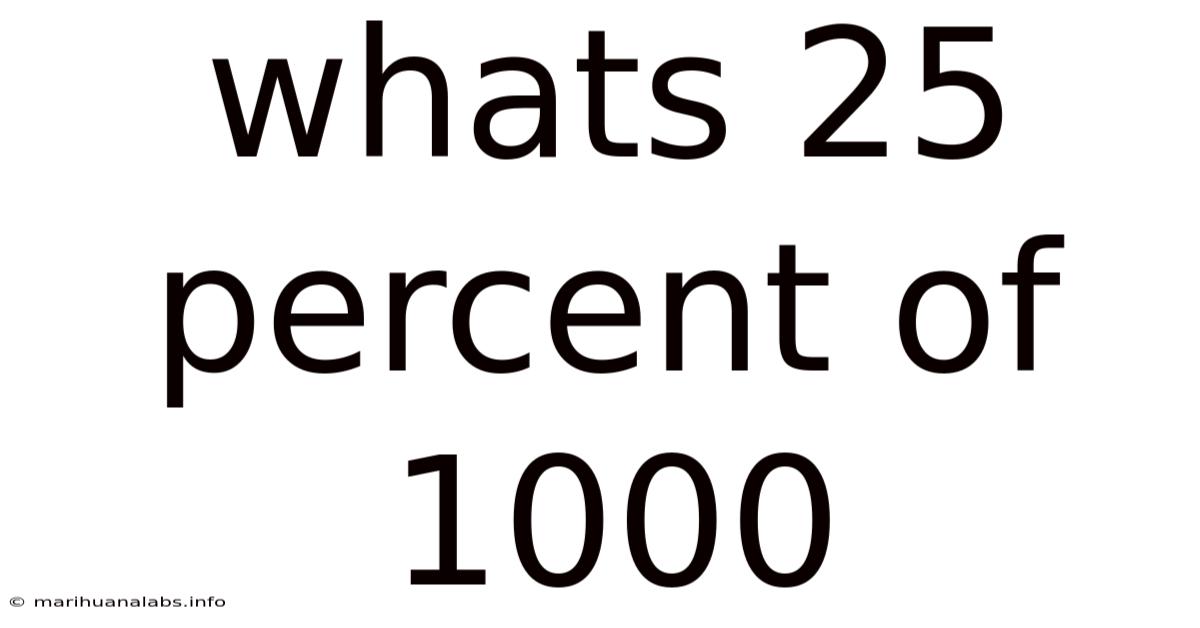
Table of Contents
What's 25 Percent of 1000? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 1000 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics: percentages. This article will not only answer the question directly but will also explore the underlying principles, various methods for solving percentage problems, and practical applications of this crucial mathematical skill in everyday life and beyond. We'll also delve into some related concepts to ensure a comprehensive understanding.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ("per cent" in Latin). So, 25% means 25 out of 100, or 25/100. This fraction can be simplified to 1/4. Understanding this fundamental relationship is crucial for solving any percentage problem.
Method 1: Using the Fraction Method
The easiest way to calculate 25% of 1000 is by using the fractional equivalent. As mentioned earlier, 25% is equal to 1/4. Therefore, finding 25% of 1000 is the same as finding 1/4 of 1000.
This can be calculated as:
(1/4) * 1000 = 250
Therefore, 25% of 1000 is 250.
Method 2: Using Decimal Conversion
Another common method involves converting the percentage to a decimal. To convert a percentage to a decimal, divide the percentage by 100. In this case:
25% ÷ 100 = 0.25
Now, multiply the decimal by the number you're finding the percentage of:
0.25 * 1000 = 250
Again, we arrive at the answer: 25% of 1000 is 250.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationships between percentages and whole numbers. We can set up a proportion:
x / 1000 = 25 / 100
Where x represents the unknown value (25% of 1000). To solve for x, we cross-multiply:
100x = 25 * 1000
100x = 25000
x = 25000 / 100
x = 250
This method confirms that 25% of 1000 is 250.
Real-World Applications of Percentage Calculations
Understanding percentages is essential in numerous real-world scenarios:
-
Financial Calculations: Calculating discounts, interest rates, taxes, tips, and profit margins all rely heavily on percentage calculations. For example, a 25% discount on a $1000 item would mean a saving of $250.
-
Data Analysis and Statistics: Percentages are used extensively in representing data in graphs, charts, and reports. For instance, understanding the percentage of students who passed an exam or the percentage market share of a company requires these calculations.
-
Scientific Applications: Percentages are used in expressing concentrations of solutions, changes in population sizes, and error margins in experiments.
-
Everyday Life: We encounter percentages constantly, from sale prices in stores to nutritional information on food labels.
Beyond the Basics: Calculating Other Percentages of 1000
While we've focused on 25%, the same methods can be applied to calculate any percentage of 1000. Let's look at a few examples:
- 10% of 1000: (10/100) * 1000 = 100 or 0.1 * 1000 = 100
- 50% of 1000: (50/100) * 1000 = 500 or 0.5 * 1000 = 500
- 75% of 1000: (75/100) * 1000 = 750 or 0.75 * 1000 = 750
- 1% of 1000: (1/100) * 1000 = 10 or 0.01 * 1000 = 10
Understanding Percentage Increase and Decrease
Percentages are also used to describe changes in values. For example:
-
Percentage Increase: If a value increases from 1000 to 1250, the percentage increase is calculated as: [(1250-1000)/1000] * 100 = 25%
-
Percentage Decrease: If a value decreases from 1000 to 750, the percentage decrease is calculated as: [(1000-750)/1000] * 100 = 25%
Frequently Asked Questions (FAQ)
-
Q: What if I need to calculate a percentage of a number other than 1000?
A: The same methods apply. Simply replace 1000 with the new number in the calculations.
-
Q: Can I use a calculator to find percentages?
A: Yes, most calculators have a percentage function (%) that simplifies these calculations.
-
Q: What if the percentage is not a whole number, like 27.5%?
A: You can still use the decimal conversion method. Convert 27.5% to 0.275 and multiply by the number.
-
Q: Why is understanding percentages important?
A: Percentages are a fundamental tool for comparing quantities, understanding proportions, and analyzing data in various fields, from finance to science.
Conclusion
Calculating 25% of 1000, resulting in 250, is a straightforward but foundational mathematical operation. This article has not only provided the answer but has also explored different methods for solving percentage problems and demonstrated the wide-ranging applications of this crucial concept in various aspects of life. Mastering percentage calculations equips you with a valuable skill set that extends far beyond simple arithmetic, empowering you to analyze data, make informed decisions, and navigate the complexities of the world around you. Remember, the key to success lies in understanding the underlying principles and practicing regularly.
Latest Posts
Latest Posts
-
Anemometer Is Used To Measure
Sep 16, 2025
-
Whats 20 Percent Of 50
Sep 16, 2025
-
How Many Inches In 600mm
Sep 16, 2025
-
Demand Pull Inflation With Diagram
Sep 16, 2025
-
Chain Of Command Business Definition
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 1000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.