What's 20 Percent Of 50
marihuanalabs
Sep 16, 2025 · 5 min read
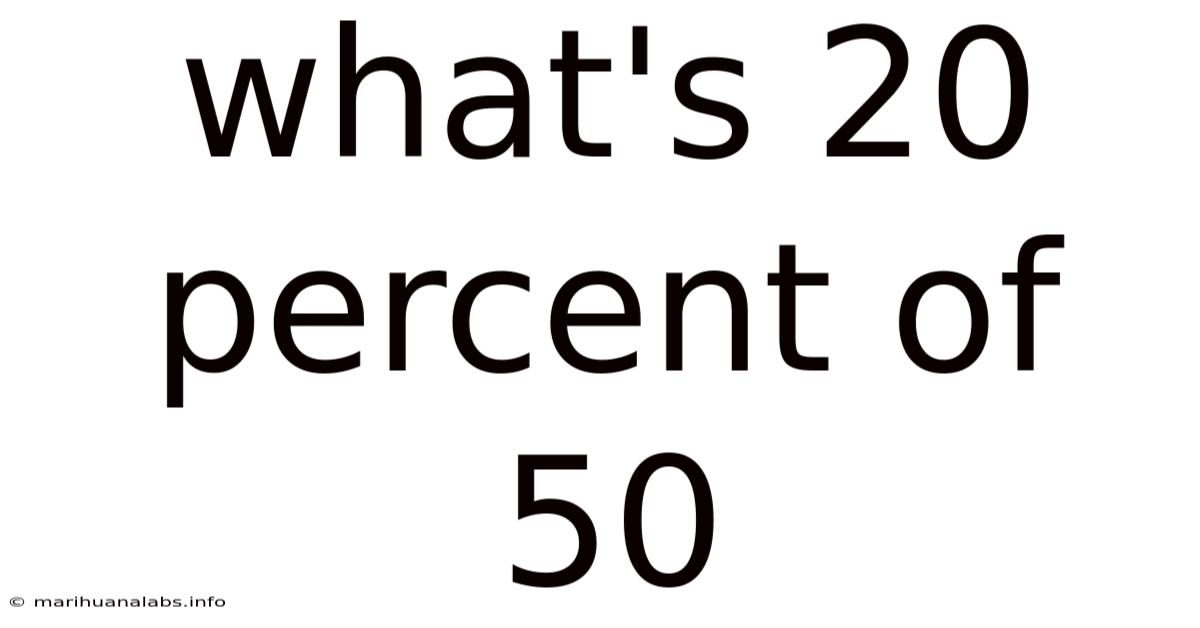
Table of Contents
What's 20 Percent of 50? A Deep Dive into Percentages and Their Applications
Finding 20 percent of 50 might seem like a simple task, easily solvable with a quick calculation. But this seemingly straightforward question opens a door to understanding a fundamental mathematical concept with wide-ranging applications in everyday life, from calculating discounts and sales tax to understanding financial reports and statistical data. This article will not only answer the question "What's 20 percent of 50?" but also explore the underlying principles of percentages, different methods for calculating them, and real-world examples to solidify your understanding.
Understanding Percentages: The Basics
A percentage is simply a fraction expressed as a part of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). So, 20 percent (written as 20%) means 20 out of 100, or 20/100. This can be simplified to the decimal 0.20 or the fraction 1/5. Understanding this fundamental relationship is crucial to solving percentage problems.
Method 1: The Direct Calculation Method
The most straightforward way to calculate 20 percent of 50 is to convert the percentage to a decimal and multiply it by the number.
-
Step 1: Convert the percentage to a decimal. To do this, divide the percentage by 100. 20% / 100 = 0.20
-
Step 2: Multiply the decimal by the number. 0.20 * 50 = 10
Therefore, 20 percent of 50 is 10.
Method 2: The Fraction Method
Alternatively, we can use the fractional representation of the percentage. As mentioned earlier, 20% is equivalent to 1/5.
-
Step 1: Express the percentage as a fraction. 20% = 20/100 = 1/5
-
Step 2: Multiply the fraction by the number. (1/5) * 50 = 50/5 = 10
Again, we arrive at the answer: 20 percent of 50 is 10.
Method 3: Using Proportions
This method is particularly useful for understanding the relationship between the parts and the whole. We can set up a proportion:
-
Step 1: Set up the proportion. We can write this as: x/50 = 20/100, where 'x' represents the unknown value (20% of 50).
-
Step 2: Cross-multiply. 100x = 20 * 50
-
Step 3: Solve for x. 100x = 1000 => x = 1000/100 = 10
This confirms once more that 20 percent of 50 is 10.
Real-World Applications: Percentage Calculations in Daily Life
The ability to calculate percentages is essential in numerous everyday scenarios. Here are a few examples:
-
Sales and Discounts: Stores frequently offer discounts like "20% off." Understanding percentage calculations allows you to quickly determine the final price of an item after a discount. For example, if a shirt costs $50 and is on sale for 20% off, you'd save $10 (20% of $50), resulting in a final price of $40.
-
Sales Tax: Sales tax is a percentage added to the price of goods and services. If the sales tax in your area is 6%, you can calculate the tax amount on a $50 purchase by finding 6% of $50, which is $3. The total cost would be $53.
-
Tips and Gratuities: When dining out, it's customary to leave a tip for the server. Calculating a 15% or 20% tip on a bill involves percentage calculations. For a $50 bill, a 20% tip would be $10.
-
Interest Calculations: Understanding percentages is vital for understanding interest rates on loans, savings accounts, and investments. The interest earned or paid is often calculated as a percentage of the principal amount.
-
Financial Statements: Financial reports, such as income statements and balance sheets, extensively use percentages to represent various financial ratios and metrics, providing insights into a company's financial health.
-
Statistics and Data Analysis: Percentages are frequently used to represent data in various forms, such as charts and graphs. Understanding percentages helps you interpret data and make informed decisions.
Beyond the Basics: Advanced Percentage Calculations
While finding 20% of 50 is a simple calculation, the principles extend to more complex scenarios. Consider these examples:
-
Finding the original amount after a percentage increase or decrease: If a price increased by 10% to $55, what was the original price? This requires working backward using the percentage.
-
Calculating percentage change: This involves determining the percentage increase or decrease between two values. For instance, if a value increased from $50 to $60, the percentage increase is calculated as ((60-50)/50) * 100% = 20%.
-
Compound interest: This involves calculating interest on both the principal amount and accumulated interest over time, resulting in exponential growth.
-
Percentage points vs. percentage change: It's crucial to differentiate between these two. A change from 20% to 25% is a 5 percentage point increase, but a 25% increase from the original 20%.
Frequently Asked Questions (FAQs)
Q: What if I need to find a percentage of a number that isn't a whole number?
A: The process remains the same. Simply convert the percentage to a decimal and multiply it by the number. For instance, to find 20% of 50.5, you would calculate 0.20 * 50.5 = 10.1.
Q: Are there any shortcuts for calculating percentages mentally?
A: Yes, several mental math tricks can help. For example, 10% of a number is easily found by moving the decimal point one place to the left. Then, you can use this to calculate other percentages. For example, 20% is double 10%, and 5% is half of 10%.
Q: What are some common mistakes to avoid when working with percentages?
A: Common errors include confusing percentage points with percentage change and incorrectly converting percentages to decimals. Always double-check your calculations and ensure you're using the correct formula.
Q: What resources can I use to improve my understanding of percentages?
A: Many online resources, textbooks, and educational videos can help. Practice solving various percentage problems to build your proficiency.
Conclusion: Mastering Percentages – A Valuable Skill
This article has demonstrated how to calculate 20 percent of 50 using different methods, emphasizing the fundamental principles of percentages. Understanding percentages is not just about solving mathematical problems; it's about developing a crucial life skill applicable in numerous contexts. From managing personal finances to interpreting data, mastering percentage calculations empowers you to make informed decisions and navigate the complexities of the world around you. Continue practicing, explore advanced applications, and embrace the versatility of this fundamental mathematical concept. Remember, the seemingly simple question, "What's 20 percent of 50?" opens doors to a much broader understanding of mathematics and its real-world applications.
Latest Posts
Latest Posts
-
Tiny Bugs In Houseplant Soil
Sep 16, 2025
-
A Net Of A Cone
Sep 16, 2025
-
Calculate Resistor For Voltage Drop
Sep 16, 2025
-
St Martin Church Cologne Germany
Sep 16, 2025
-
Indigenous Tribes In New Zealand
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What's 20 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.