What Is 70 Of 15
marihuanalabs
Sep 13, 2025 · 5 min read
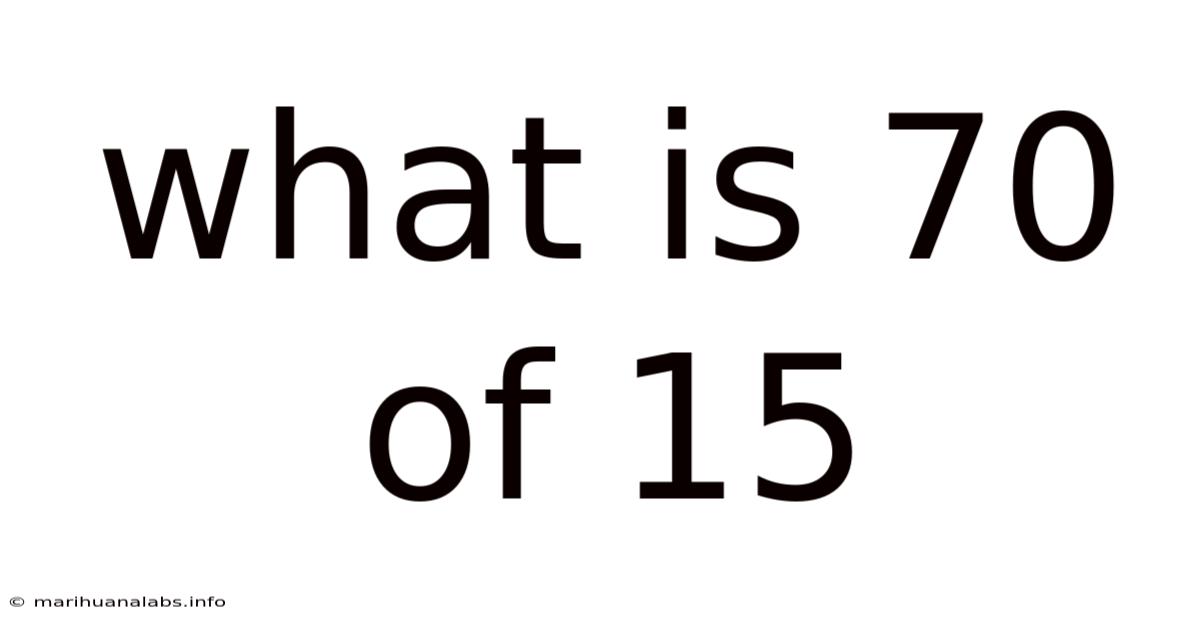
Table of Contents
What is 70% of 15? A Deep Dive into Percentages and Their Applications
Finding 70% of 15 might seem like a simple arithmetic problem, easily solvable with a calculator. However, understanding the underlying concepts of percentages and their applications opens doors to a world of mathematical problem-solving and real-world applications. This article will not only provide the answer but will also delve into the methods of calculating percentages, explore different approaches, and discuss the relevance of percentage calculations in various fields. We'll move beyond the simple calculation and unpack the broader significance of percentage understanding.
Understanding Percentages: The Fundamentals
A percentage is a fraction or ratio expressed as a number out of 100. The term "percent" literally means "per hundred" or "out of one hundred." The symbol % is used to denote percentages. Therefore, 70% can be written as 70/100 or 0.7. This fundamental understanding is crucial for tackling any percentage calculation.
Methods for Calculating 70% of 15
There are several ways to calculate 70% of 15. Let's explore the most common methods:
1. The Decimal Method:
This is arguably the most straightforward approach. We convert the percentage to a decimal and then multiply it by the number.
- Step 1: Convert 70% to a decimal: 70% = 70/100 = 0.7
- Step 2: Multiply the decimal by 15: 0.7 * 15 = 10.5
Therefore, 70% of 15 is 10.5.
2. The Fraction Method:
This method involves expressing the percentage as a fraction and then performing the multiplication.
- Step 1: Express 70% as a fraction: 70% = 70/100
- Step 2: Simplify the fraction (optional, but helpful): 70/100 simplifies to 7/10
- Step 3: Multiply the fraction by 15: (7/10) * 15 = 105/10 = 10.5
Again, the result is 10.5.
3. The Proportion Method:
This method sets up a proportion to solve for the unknown value.
- Step 1: Set up a proportion: 70/100 = x/15 (where x represents 70% of 15)
- Step 2: Cross-multiply: 70 * 15 = 100 * x
- Step 3: Solve for x: 1050 = 100x => x = 1050/100 = 10.5
This method reinforces the concept of ratios and proportions, offering a more visual understanding of the problem.
Beyond the Calculation: Applications of Percentages
The seemingly simple calculation of 70% of 15 has far-reaching applications in various fields. Understanding percentages is essential in:
-
Finance: Calculating interest rates, discounts, taxes, profit margins, and investment returns all rely heavily on percentage calculations. For instance, if a bank offers a 7% annual interest rate on a savings account, you would use percentage calculations to determine the interest earned on your deposit. Similarly, calculating sales tax involves finding a percentage of the purchase price.
-
Business: Businesses use percentages to analyze sales data, track market share, assess profitability, and forecast future performance. Understanding percentage change (increase or decrease) is crucial for evaluating business trends and making informed decisions. For example, if a business's sales increased by 15% compared to the previous year, percentage calculations help quantify this growth.
-
Science and Statistics: Percentages are frequently used to represent data in scientific studies and statistical analyses. For instance, researchers might express the percentage of participants who responded positively to a treatment in a clinical trial. Data representation using percentages facilitates easier comparison and understanding of results.
-
Everyday Life: From calculating tips in restaurants to understanding sale discounts in stores, percentages are an integral part of our daily lives. Knowing how to calculate percentages efficiently enables informed consumer decisions. For instance, understanding that a 20% discount on a $50 item saves you $10 allows for better budgeting and cost-effectiveness.
-
Education: Percentages are fundamental in evaluating academic performance. Grade point averages (GPAs), test scores, and class rankings are often expressed as percentages. Understanding percentages helps students track their progress, identify areas for improvement, and understand their overall academic standing.
Expanding Your Understanding: Further Exploration
Let's explore some related concepts that build upon the understanding of calculating 70% of 15:
-
Percentage Increase and Decrease: These calculations determine the change in a value as a percentage of the original value. For example, if a price increases from $10 to $15, the percentage increase is 50% [(15-10)/10 * 100%].
-
Percentage Points: This concept clarifies the difference between a percentage change and a change in percentage points. For example, if an interest rate rises from 5% to 7%, the percentage point increase is 2 percentage points, not 40%.
-
Compounding Percentages: This involves calculating percentages on a changing base. Compound interest is a prime example where interest earned in one period is added to the principal, and the next period's interest is calculated on this larger amount.
Frequently Asked Questions (FAQ)
-
Q: How do I calculate a different percentage of 15?
- A: Follow the same methods outlined above, simply substituting your desired percentage for 70%. For instance, to find 25% of 15, you would calculate (25/100) * 15 or 0.25 * 15 = 3.75.
-
Q: What if I need to find 70% of a larger number?
- A: The methods remain the same; simply replace 15 with your larger number. The decimal method is often the easiest: convert 70% to 0.7 and multiply by the new number.
-
Q: Are there any online calculators for percentages?
- A: Yes, many websites and apps offer percentage calculators. These can be helpful for quick calculations, but it's crucial to understand the underlying principles to solve problems independently.
-
Q: Why is understanding percentages important?
- A: Percentages are a fundamental mathematical concept with widespread applications in various fields, making them essential for financial literacy, critical thinking, and informed decision-making.
Conclusion
Calculating 70% of 15 is a stepping stone to a much broader understanding of percentages and their importance. While the answer is 10.5, the real value lies in mastering the methods, appreciating the diverse applications, and recognizing the power of percentage calculations in navigating the numerical world around us. By grasping these concepts, you equip yourself with a valuable skill that extends far beyond simple arithmetic. The ability to confidently perform percentage calculations translates into greater financial awareness, more effective decision-making in various contexts, and a deeper comprehension of the numerical data that shapes our world.
Latest Posts
Latest Posts
-
6 Divided By 2 5
Sep 14, 2025
-
Positive Consumption Externality Diagram Explained
Sep 14, 2025
-
Ken Follett The Kingsbridge Novels
Sep 14, 2025
-
She Stoops To Conquer Summary
Sep 14, 2025
-
What Is Espionage In Iran
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about What Is 70 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.