6 Divided By 2 5
marihuanalabs
Sep 14, 2025 · 7 min read
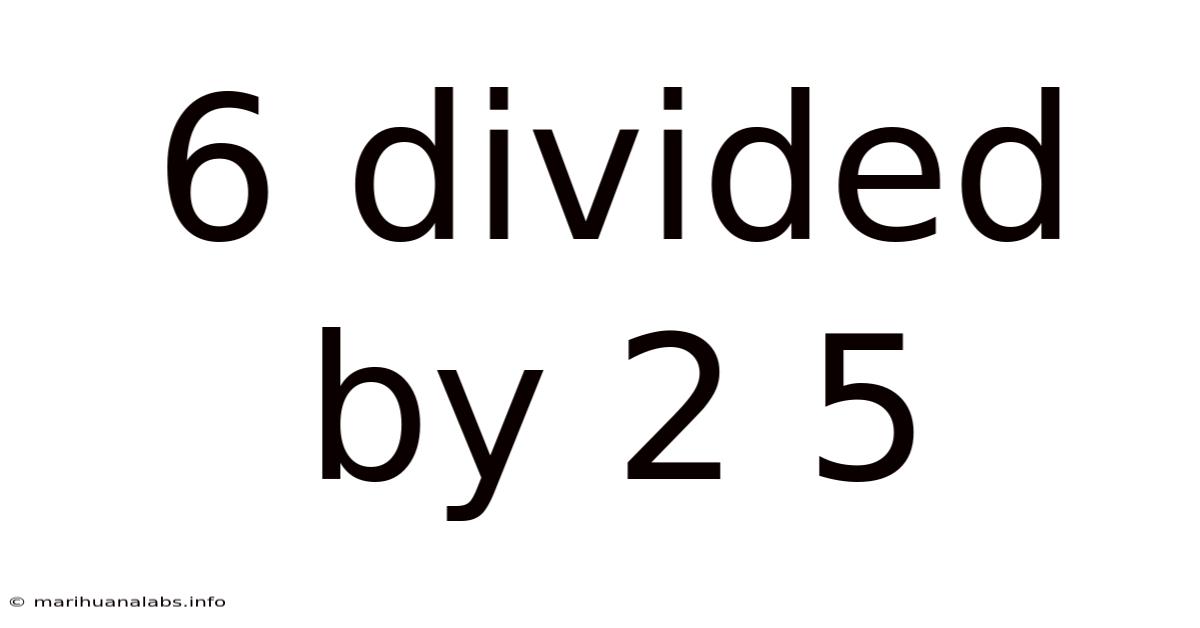
Table of Contents
Decoding 6 ÷ 2(5): A Deep Dive into Order of Operations
The seemingly simple mathematical expression "6 ÷ 2(5)" has sparked countless debates online, highlighting a critical misunderstanding of the order of operations. This article will delve into the correct method for solving this problem, explaining the underlying principles and addressing common misconceptions. Understanding the order of operations is crucial not just for solving this specific puzzle but for mastering more complex mathematical calculations. This exploration will clarify the ambiguity and provide a solid understanding of mathematical precedence.
Introduction: The Order of Operations – PEMDAS/BODMAS
The key to correctly solving 6 ÷ 2(5) lies in understanding the order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction). Both acronyms represent the same fundamental rules:
- Parentheses/Brackets: Calculations within parentheses or brackets should always be performed first.
- Exponents/Orders: Exponents (powers) or roots are evaluated next.
- Multiplication and Division: These operations have equal precedence and are performed from left to right.
- Addition and Subtraction: These operations also have equal precedence and are performed from left to right.
The crucial point often missed is the equal precedence of multiplication and division (and addition and subtraction). This means we don't prioritize multiplication over division or vice versa; we simply work from left to right.
Step-by-Step Solution to 6 ÷ 2(5)
Applying PEMDAS/BODMAS to 6 ÷ 2(5):
-
No Parentheses (Brackets): There are no parentheses containing multiple operations. However, implicit multiplication exists between the 2 and the 5. This is crucial. We can rewrite the expression to make this explicit: 6 ÷ 2 * 5
-
No Exponents (Orders): There are no exponents in this expression.
-
Multiplication and Division (Left to Right): Following the left-to-right rule, we perform division first:
6 ÷ 2 = 3
The expression now becomes: 3 * 5
-
Multiplication: Finally, we perform the multiplication:
3 * 5 = 15
Therefore, the correct answer to 6 ÷ 2(5) is 15.
Addressing Common Misconceptions
The confusion surrounding this problem often stems from a misinterpretation of implied multiplication. Some argue that multiplication adjacent to parentheses should always take precedence. This is incorrect. While implicit multiplication might be visually grouped with the parenthesis, it doesn't inherently have higher precedence than explicit division or multiplication in the absence of parentheses encompassing a larger expression.
-
Misconception 1: Multiplication always comes before division: This is false. Multiplication and division have equal precedence, and their order is determined by their position from left to right within the expression.
-
Misconception 2: Implied multiplication has higher precedence: The placement of the 2 next to the parenthesis does not automatically grant it higher precedence. The expression is interpreted as 6 ÷ 2 x 5, with equal precedence for division and multiplication.
-
Misconception 3: Incorrect use of distributive property: The distributive property (a(b + c) = ab + ac) is not applicable here, because there's no addition or subtraction within the parentheses.
The Importance of Clarity and Notation
The ambiguity surrounding expressions like 6 ÷ 2(5) highlights the importance of clear and unambiguous mathematical notation. In more advanced mathematics, different notations and conventions might exist, leading to different interpretations. However, following the standard order of operations (PEMDAS/BODMAS) as universally taught avoids this ambiguity. Using additional parentheses or writing the expression in a fractional format would eliminate any potential for misinterpretation:
- Using parentheses for clarity: (6 ÷ 2) * 5 = 15 clarifies the intended order.
- Fractional notation: 6 / (2 * 5) = 6/10 = 0.6. This is a different expression entirely.
Therefore, using proper notation is crucial to communicate mathematical operations accurately and avoid misinterpretations.
A Deeper Dive: Different Interpretations and Historical Context
While the standard interpretation, based on PEMDAS/BODMAS, yields 15, some older textbooks and interpretations might lead to a different result. This stems from historical variations in mathematical notation and the evolution of mathematical conventions. Older textbooks sometimes treated implicit multiplication as having higher precedence, although this is not a universally accepted modern convention. It's important to note that even within the context of the older interpretations, the ambiguity is highlighted, thus reinforcing the necessity for clear notation.
The crucial factor is the understanding and adherence to a consistent set of rules. While historical context provides a fascinating perspective on the evolution of mathematical notation, adhering to contemporary standards ensures consistent and unambiguous results.
Mathematical Properties and Their Relevance
Let's briefly review some key mathematical properties to further illustrate why the left-to-right approach is correct in the context of 6 ÷ 2(5):
-
Associative Property: This property applies to addition and multiplication but not to subtraction or division. The associative property states that the grouping of numbers does not change the result for addition or multiplication: (a + b) + c = a + (b + c) and (a * b) * c = a * (b * c). This is not applicable to 6 ÷ 2(5).
-
Commutative Property: This property applies to addition and multiplication, stating that the order of numbers does not affect the result: a + b = b + a and a * b = b * a. However, this is not applicable to division or subtraction.
-
Distributive Property: This property involves multiplication over addition or subtraction: a(b + c) = ab + ac. This is not directly relevant to the expression 6 ÷ 2(5) as there's no addition or subtraction within the parentheses.
Understanding these properties helps to highlight the limitations of applying them to the expression and reinforces the importance of adhering to the strict order of operations.
Frequently Asked Questions (FAQ)
Q1: Why is the left-to-right rule important here?
A1: Multiplication and division have equal precedence. The left-to-right rule dictates that we perform the operation that appears first in the expression. This is a fundamental principle of the order of operations.
Q2: Can I use a calculator to solve this?
A2: The result might vary depending on the calculator and its programming. Some calculators might follow the left-to-right rule correctly, resulting in 15, while others might prioritize implicit multiplication, incorrectly resulting in a different answer. Therefore, relying solely on a calculator without understanding the order of operations can be misleading.
Q3: What if the expression was written differently? For example, 6 / 2 * 5?
A3: Using the forward slash (/) instead of the division symbol (÷) does not change the order of operations. The expression 6 / 2 * 5 is solved exactly the same way as 6 ÷ 2 * 5, resulting in 15.
Q4: Are there any exceptions to PEMDAS/BODMAS?
A4: While PEMDAS/BODMAS is the generally accepted standard, there might be subtle variations or conventions in specialized areas of mathematics. However, for general mathematical calculations, adhering to PEMDAS/BODMAS ensures consistency and avoids ambiguity.
Q5: How can I avoid making similar mistakes in the future?
A5: Practice regularly using the order of operations. When encountering complex expressions, break them down into smaller, simpler steps. Use parentheses to clarify the intended order of operations if there is any ambiguity.
Conclusion: The Power of Precision in Mathematics
The expression 6 ÷ 2(5) serves as a powerful reminder of the importance of understanding and correctly applying the order of operations. The seemingly simple problem highlights the need for clear notation and emphasizes the equal precedence of multiplication and division, with the order determined by their left-to-right position. By correctly applying PEMDAS/BODMAS, we arrive at the solution 15. Mastering the order of operations is crucial for building a strong foundation in mathematics and solving increasingly complex problems with accuracy and confidence. Remember that clear communication through proper notation is just as essential as understanding the underlying mathematical principles. Practice and careful attention to detail will make you more proficient and confident in your mathematical skills.
Latest Posts
Latest Posts
-
Prime Factor Tree For 90
Sep 14, 2025
-
Volume Of Pyramid Triangular Base
Sep 14, 2025
-
Conjugation Of Spanish Verb Ver
Sep 14, 2025
-
Atlas Mountains On A Map
Sep 14, 2025
-
What Is 18mm In Inches
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 6 Divided By 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.