Prime Factor Tree For 90
marihuanalabs
Sep 14, 2025 · 5 min read
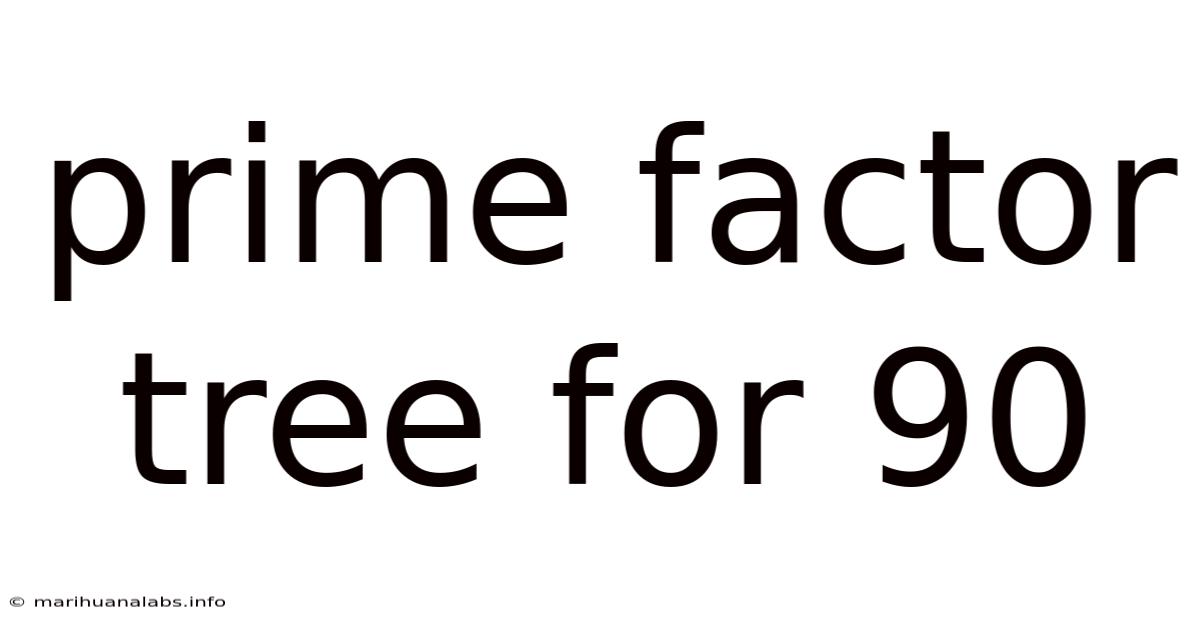
Table of Contents
Unveiling the Prime Factors of 90: A Deep Dive into Prime Factorization using Factor Trees
Finding the prime factors of a number might seem like a simple task, especially for smaller numbers like 90. However, understanding the process of prime factorization, and specifically how to use a prime factor tree, provides a foundational understanding of number theory and its applications in mathematics and computer science. This article will guide you through the process of finding the prime factors of 90 using a factor tree, explaining the underlying concepts in a clear and accessible way, and delving deeper into the significance of prime factorization. We'll also explore common misconceptions and answer frequently asked questions.
What is Prime Factorization?
Prime factorization is the process of breaking down a composite number (a number greater than 1 that is not prime) into its prime factors. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples of prime numbers include 2, 3, 5, 7, 11, and so on. The fundamental theorem of arithmetic states that every composite number can be expressed as a unique product of prime numbers. This unique representation is crucial in many areas of mathematics.
Understanding the Prime Factor Tree Method
The prime factor tree is a visual method for finding the prime factorization of a number. It involves repeatedly dividing the number by its smallest prime factor until you are left with only prime numbers. Let's illustrate this with the number 90.
Step-by-Step Prime Factorization of 90 using a Factor Tree
1. Start with the Number: Begin with the number you want to factorize, which in our case is 90. Write it at the top of your factor tree.
2. Find the Smallest Prime Factor: Identify the smallest prime number that divides evenly into 90. This is 2.
3. Branch Out: Draw two branches extending down from 90. On one branch, write the prime factor (2), and on the other branch, write the result of 90 divided by 2 (45).
4. Repeat the Process: Now, focus on the number 45. The smallest prime factor of 45 is 3. Draw two branches from 45. Write 3 on one branch and 15 (45/3) on the other.
5. Continue Until All Branches End in Prime Numbers: Continue this process. The smallest prime factor of 15 is 3. Divide 15 by 3, resulting in 5. Since 5 is a prime number, you've reached the end of that branch.
6. The Prime Factorization: Once all branches end in prime numbers, you have completed the prime factorization. In our case, the prime factors of 90 are 2, 3, 3, and 5.
Here's a visual representation of the prime factor tree for 90:
90
/ \
2 45
/ \
3 15
/ \
3 5
Therefore, the prime factorization of 90 is 2 x 3 x 3 x 5, or 2 x 3² x 5.
Why is Prime Factorization Important?
The seemingly simple act of prime factorization has significant implications across various mathematical fields and practical applications:
-
Simplifying Fractions: Prime factorization is essential for simplifying fractions to their lowest terms. By finding the prime factors of the numerator and denominator, you can easily identify common factors and cancel them out.
-
Finding the Least Common Multiple (LCM) and Greatest Common Divisor (GCD): Prime factorization provides an efficient way to calculate the LCM and GCD of two or more numbers. The LCM is the smallest number that is a multiple of all the given numbers, while the GCD is the largest number that divides all the given numbers without leaving a remainder.
-
Cryptography: Prime numbers play a crucial role in cryptography, the art of secure communication. Many encryption algorithms rely on the difficulty of factoring very large numbers into their prime factors. The security of these systems depends on the computational infeasibility of factoring large composite numbers.
-
Abstract Algebra: Prime factorization forms the basis of many concepts in abstract algebra, a branch of mathematics that deals with algebraic structures such as groups, rings, and fields.
-
Number Theory: Prime factorization is fundamental to number theory, the study of the properties of integers. Many theorems and conjectures in number theory revolve around prime numbers and their distribution.
Common Mistakes to Avoid When Creating a Prime Factor Tree
-
Using Composite Numbers: Ensure you only use prime numbers when branching out from the main number. Using composite numbers will lead to an incorrect factorization.
-
Missing Prime Factors: Carefully check each number to ensure you've identified all its prime factors. Skipping a prime factor will result in an incomplete factorization.
-
Incorrect Division: Double-check your division at each step to avoid calculation errors. A single mistake in division can throw off the entire factorization.
Alternative Methods for Prime Factorization
While the prime factor tree is a visually intuitive method, other techniques can achieve the same result:
-
Division Method: Repeatedly divide the number by its smallest prime factor until you reach 1. The prime factors used in the division process form the prime factorization.
-
Using a Calculator: Some calculators have built-in functions for prime factorization, making the process faster, especially for larger numbers.
Frequently Asked Questions (FAQ)
Q1: What if I choose a different prime factor to start with?
A1: While you can start with a different prime factor, the final prime factorization will always be the same (due to the Fundamental Theorem of Arithmetic). However, the factor tree might look different. The order of the prime factors doesn't change the result.
Q2: Can a number have only one prime factor?
A2: Yes, a prime number itself has only one prime factor—itself.
Q3: Is there a limit to how large a number can be prime factorized?
A3: Theoretically, there is no limit. However, practically, the process can become computationally intensive for extremely large numbers.
Conclusion
Prime factorization, while seemingly basic, is a cornerstone concept in mathematics. The prime factor tree method provides a clear and accessible way to understand and perform this vital process. Mastering prime factorization not only helps in solving specific mathematical problems but also enhances your overall understanding of number theory and its diverse applications in various fields. Understanding the prime factorization of numbers like 90 (2 x 3² x 5) is fundamental to advanced mathematical concepts and problem-solving. By carefully following the steps and avoiding common pitfalls, you can confidently tackle any prime factorization challenge. Remember, practice makes perfect! The more you work with prime factor trees, the more comfortable and proficient you will become.
Latest Posts
Latest Posts
-
How To Do An Autobiography
Sep 14, 2025
-
Poem Daffodils By William Wordsworth
Sep 14, 2025
-
Chapter 4 Summary Animal Farm
Sep 14, 2025
-
Example Of A Tree Diagram
Sep 14, 2025
-
The History Of Bees Book
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Prime Factor Tree For 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.