What Is 25 Of 10
marihuanalabs
Sep 19, 2025 · 5 min read
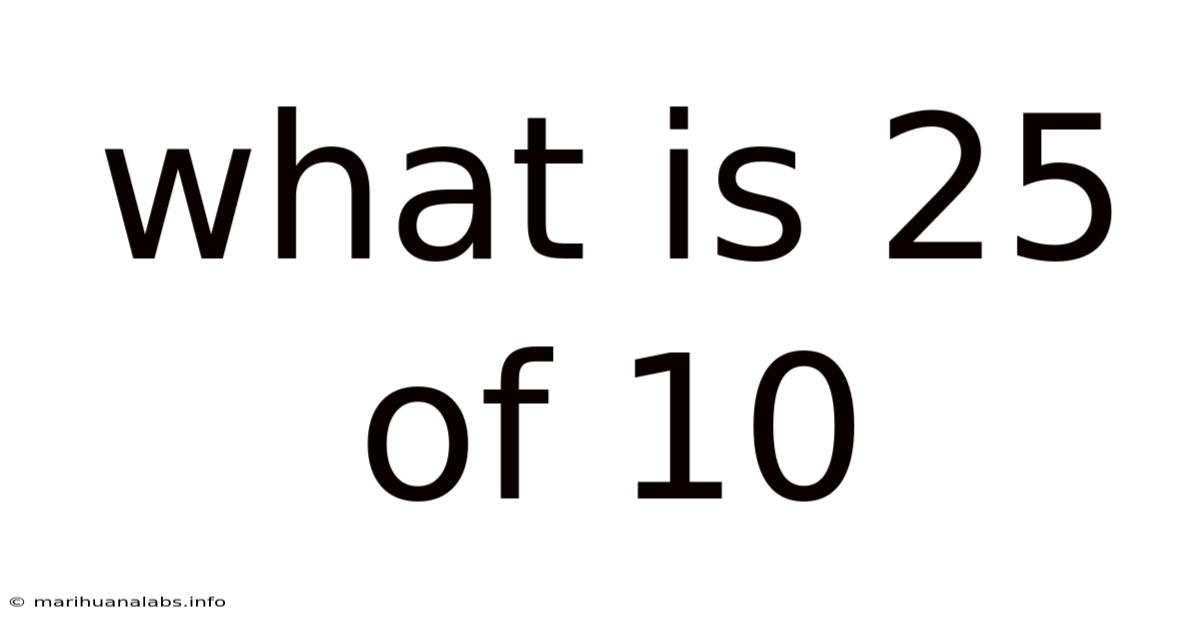
Table of Contents
What is 25% of 10? Understanding Percentages and Practical Applications
This article will thoroughly explore the question "What is 25% of 10?" We'll delve into the fundamental concepts of percentages, providing a step-by-step guide to solving this problem and similar calculations. Furthermore, we'll explore the practical applications of percentage calculations in everyday life, from calculating discounts to understanding financial statements. By the end, you'll not only know the answer but also possess a strong understanding of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" is used to represent percentages. For example, 25% means 25 out of 100, which can also be written as the fraction 25/100 or the decimal 0.25. Understanding this fundamental concept is crucial for solving percentage problems.
Calculating 25% of 10: A Step-by-Step Guide
There are several ways to calculate 25% of 10. Let's explore the most common methods:
Method 1: Using the Fraction Equivalent
As mentioned earlier, 25% is equivalent to the fraction 25/100. To find 25% of 10, we can simply multiply 10 by the fraction 25/100:
10 * (25/100) = 2.5
Therefore, 25% of 10 is 2.5.
Method 2: Using Decimal Equivalents
Another approach involves converting the percentage to its decimal equivalent. Since 25% is equal to 0.25, we can multiply 10 by 0.25:
10 * 0.25 = 2.5
This method yields the same result: 25% of 10 is 2.5.
Method 3: Using Proportions
We can also solve this using proportions. We can set up a proportion where 'x' represents the unknown value (25% of 10):
25/100 = x/10
To solve for x, we can cross-multiply:
25 * 10 = 100 * x
250 = 100x
x = 250/100
x = 2.5
Again, we arrive at the same answer: 25% of 10 is 2.5.
Practical Applications of Percentage Calculations
Percentage calculations are used extensively in various aspects of daily life and professional fields. Here are a few examples:
-
Discounts: Retail stores frequently offer discounts expressed as percentages. For example, a 20% discount on a $50 item means you'll save 20% of $50, which is $10.
-
Taxes: Sales tax is a percentage added to the price of goods and services. Understanding percentage calculations helps you determine the final price after tax is included.
-
Tips: Calculating tips in restaurants often involves determining a percentage of the total bill. A 15% tip on a $30 meal is $4.50 (15% of $30 = $4.50).
-
Interest Rates: Interest rates on loans and investments are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions.
-
Grade Calculations: Many educational systems use percentages to represent grades. A score of 85% on a test indicates that you answered 85 out of 100 questions correctly.
-
Financial Statements: Businesses use percentage calculations to analyze financial data, such as profit margins, growth rates, and debt ratios.
Understanding Percentage Increase and Decrease
Percentage calculations aren't just about finding a portion of a number. They also extend to understanding percentage increases and decreases. Let's consider two scenarios:
Scenario 1: Percentage Increase
Suppose a product initially costs $10, and its price increases by 25%. To calculate the new price:
- Calculate the increase: 25% of $10 = $2.50
- Add the increase to the original price: $10 + $2.50 = $12.50
The new price after a 25% increase is $12.50.
Scenario 2: Percentage Decrease
Imagine a product initially costs $10 and its price decreases by 25%. To calculate the new price:
- Calculate the decrease: 25% of $10 = $2.50
- Subtract the decrease from the original price: $10 - $2.50 = $7.50
The new price after a 25% decrease is $7.50.
Solving More Complex Percentage Problems
While calculating 25% of 10 is relatively straightforward, more complex percentage problems might require a slightly different approach. Let's explore a few examples:
Example 1: Finding the Original Value
If 25% of a number is 5, what is the number?
Let's represent the unknown number as 'x'. We can set up the equation:
0.25x = 5
To solve for x, divide both sides by 0.25:
x = 5 / 0.25 = 20
Therefore, the original number is 20.
Example 2: Calculating Percentage Change
If a value increases from 10 to 12.5, what is the percentage increase?
- Calculate the difference: 12.5 - 10 = 2.5
- Divide the difference by the original value: 2.5 / 10 = 0.25
- Multiply by 100 to express as a percentage: 0.25 * 100 = 25%
The percentage increase is 25%.
Advanced Percentage Concepts
For a more in-depth understanding, consider exploring advanced concepts like compound interest, which involves earning interest on both the principal and accumulated interest. Understanding exponential growth and decay, which are often modeled using percentages, is also beneficial for various applications.
Frequently Asked Questions (FAQ)
Q: What is the easiest way to calculate percentages?
A: The easiest way often depends on the specific problem. Using decimal equivalents is generally quick and efficient for simple calculations. For more complex problems, setting up a proportion can be helpful.
Q: How do I calculate percentages without a calculator?
A: You can perform manual calculations using fractions and basic arithmetic. Remember that 10% of a number is simply one-tenth of the number. You can use this as a base to calculate other percentages. For instance, 20% is double 10%, and 5% is half of 10%.
Q: Are there any online tools or calculators to help with percentage calculations?
A: Yes, many online calculators are available to assist with percentage calculations. These can be particularly helpful for more complex problems or when speed is essential.
Conclusion
In conclusion, 25% of 10 is 2.5. This seemingly simple calculation forms the foundation for a wide range of applications in everyday life and various fields. Understanding the core concepts of percentages, along with the different methods for calculation, empowers you to tackle a diverse array of percentage problems with confidence. Whether calculating discounts, understanding financial statements, or making informed decisions in various aspects of life, a solid grasp of percentages is an invaluable skill. Remember to practice regularly to solidify your understanding and build your proficiency in this essential mathematical concept.
Latest Posts
Latest Posts
-
Novels Like The Kite Runner
Sep 19, 2025
-
Segmental And Subsegmental Pulmonary Embolism
Sep 19, 2025
-
Snake In A Monkeys Shadow
Sep 19, 2025
-
What Is 150 Of 30
Sep 19, 2025
-
Cubic Meter To Gallon Conversion
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 25 Of 10 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.