What Is 150 Of 30
marihuanalabs
Sep 19, 2025 · 5 min read
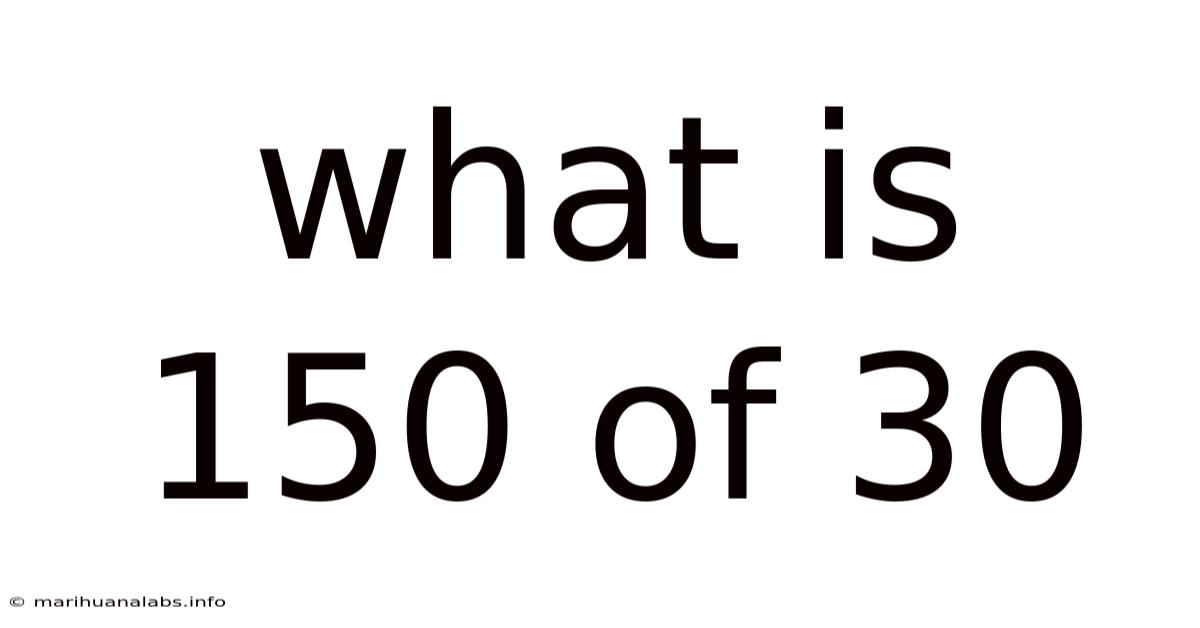
Table of Contents
What is 150% of 30? Understanding Percentages and Their Applications
Finding 150% of 30 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for a wide range of applications, from everyday budgeting and shopping to complex financial analysis and scientific calculations. This article will not only solve this specific problem but also delve into the broader concept of percentages, offering explanations, examples, and practical applications to solidify your understanding.
Understanding Percentages: A Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin phrase "per centum," meaning "out of a hundred." Therefore, 150% signifies 150 parts out of 100, or 1.5 times the original value. Understanding this fundamental concept is key to solving percentage problems.
We represent percentages using the symbol '%'. To convert a percentage to a decimal, we divide the percentage by 100. For instance, 150% becomes 150/100 = 1.5. Conversely, to convert a decimal to a percentage, we multiply the decimal by 100.
Calculating 150% of 30: Step-by-Step
Now, let's tackle the question: What is 150% of 30? We can approach this problem in several ways:
Method 1: Using the Decimal Equivalent
- Convert the percentage to a decimal: 150% = 150/100 = 1.5
- Multiply the decimal by the number: 1.5 * 30 = 45
Therefore, 150% of 30 is 45.
Method 2: Using Fractions
- Convert the percentage to a fraction: 150% = 150/100 = 3/2
- Multiply the fraction by the number: (3/2) * 30 = 45
This method demonstrates the fractional representation of percentages, further solidifying the concept.
Method 3: Breaking it Down
We can also break down the calculation into smaller, more manageable steps. 100% of 30 is 30. Since we want 150%, we can calculate 50% of 30 separately and add it to the 100%.
- Calculate 50% of 30: 50% = 0.5, so 0.5 * 30 = 15
- Add 100% and 50%: 30 + 15 = 45
This method provides a visual understanding of how percentages build upon each other.
Real-World Applications of Percentage Calculations
The ability to calculate percentages is a highly practical skill with widespread applications. Here are a few examples:
-
Finance: Calculating interest rates, discounts, tax amounts, profit margins, and investment returns all involve percentage calculations. Understanding these concepts is fundamental for managing personal finances and making informed financial decisions. For example, if you're considering a loan with a 5% interest rate, you need to understand how that percentage translates into actual monetary cost.
-
Retail and Sales: Discounts are frequently expressed as percentages. Calculating the final price after a discount requires a simple percentage calculation. Sales tax is also a percentage applied to the price of goods. Understanding these percentage calculations is crucial for budget planning.
-
Science and Statistics: Percentages are essential for expressing probabilities, proportions, and rates of change in scientific research and statistical analysis. This includes expressing data such as growth rates, error margins, and statistical significance.
-
Everyday Life: Calculating tips at restaurants, understanding nutritional information (e.g., percentage of daily value), and interpreting survey results all involve working with percentages.
Beyond the Basics: More Complex Percentage Problems
While calculating 150% of 30 is a straightforward example, percentage problems can become more complex. Let's explore some variations:
-
Finding the Percentage: Instead of finding the percentage of a number, you might need to determine what percentage one number represents of another. For example, "What percentage of 60 is 15?" To solve this, you would divide 15 by 60 and multiply by 100: (15/60) * 100 = 25%.
-
Finding the Original Value: You might know the result of a percentage increase or decrease and the percentage itself, but need to find the original value. For example, "A price increased by 20% to $60. What was the original price?" This involves solving an equation: Original Price * 1.20 = $60. The original price is $60 / 1.20 = $50.
-
Percentage Change: Calculating the percentage change between two values is important for tracking growth or decline. The formula is: [(New Value - Old Value) / Old Value] * 100%. For example, if sales increased from $100 to $120, the percentage increase is [(120 - 100) / 100] * 100% = 20%.
These more complex scenarios illustrate the diverse applications of percentage calculations in various contexts.
Practical Tips for Mastering Percentages
Here are some practical tips to improve your skills in working with percentages:
-
Practice Regularly: The best way to become proficient in percentage calculations is to practice regularly with a variety of problems.
-
Use Multiple Methods: Try solving the same problem using different methods to gain a deeper understanding and to ensure accuracy.
-
Visual Aids: Use visual aids like diagrams or charts to represent the problem visually. This can be particularly helpful when working with more complex scenarios.
-
Check Your Work: Always double-check your calculations to avoid errors.
-
Use a Calculator: While understanding the underlying principles is essential, don't hesitate to use a calculator for more complex calculations or to save time.
Frequently Asked Questions (FAQ)
-
What does "percent" mean? "Percent" means "out of one hundred".
-
How do I convert a percentage to a decimal? Divide the percentage by 100.
-
How do I convert a decimal to a percentage? Multiply the decimal by 100.
-
What are some common mistakes when working with percentages? Common mistakes include incorrect decimal placement, forgetting to multiply or divide by 100, and misinterpreting the problem.
-
Where can I find more practice problems? Many websites and textbooks offer practice problems on percentages.
Conclusion
Calculating 150% of 30 is a simple yet fundamental percentage calculation. Mastering this concept and understanding the broader principles of percentages is crucial for navigating various aspects of life, from personal finance to professional endeavors. By applying the methods outlined in this article and practicing regularly, you can build confidence and competence in tackling percentage problems of all levels of complexity. Remember that the key lies in understanding the underlying concepts and applying them strategically to solve a variety of percentage-related problems. The ability to confidently work with percentages is a valuable skill that will serve you well in many areas of life.
Latest Posts
Latest Posts
-
Quotes In Waiting For Godot
Sep 19, 2025
-
How Much Is 1 Gross
Sep 19, 2025
-
Margaret Dashwood Sense And Sensibility
Sep 19, 2025
-
That Was Good In German
Sep 19, 2025
-
Characteristics Of The Tragic Hero
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 150 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.