Lcm Of 7 And 9
marihuanalabs
Sep 24, 2025 · 6 min read
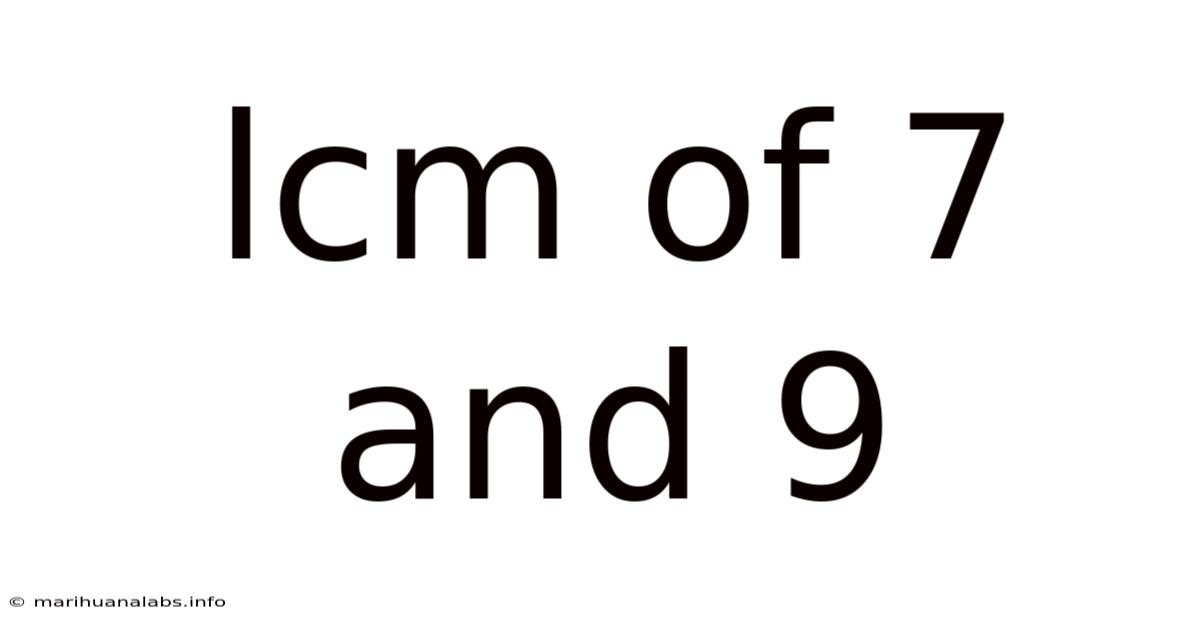
Table of Contents
Understanding the Least Common Multiple (LCM) of 7 and 9: A Comprehensive Guide
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it provides a solid foundation for more advanced mathematical concepts. This article delves into the LCM of 7 and 9, explaining various approaches, exploring their applications, and addressing common queries. Whether you're a student brushing up on your math skills or an educator looking for a comprehensive explanation, this guide provides a clear and detailed understanding of the LCM, specifically focusing on the LCM of 7 and 9.
Introduction to Least Common Multiple (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that contains all the numbers you're considering as factors. This concept is fundamental in various areas of mathematics, including fractions, simplifying expressions, and solving problems involving ratios and proportions. Understanding LCM is crucial for tasks ranging from simple fraction addition to more complex algebraic manipulations. We'll explore different methods to calculate the LCM, focusing on the specific example of finding the LCM of 7 and 9.
Method 1: Listing Multiples
The most straightforward method to find the LCM is by listing the multiples of each number until a common multiple is found. Let's apply this to find the LCM of 7 and 9:
- Multiples of 7: 7, 14, 21, 28, 35, 42, 49, 56, 63, 70, 77, 84, 91, 98, 105, 112, 119, 126...
- Multiples of 9: 9, 18, 27, 36, 45, 54, 63, 72, 81, 90, 99, 108, 117, 126...
Notice that the smallest number that appears in both lists is 63. Therefore, the LCM of 7 and 9 is 63. This method works well for smaller numbers, but it can become cumbersome and time-consuming for larger numbers.
Method 2: Prime Factorization
A more efficient method, especially for larger numbers, involves prime factorization. This method breaks down each number into its prime factors – numbers divisible only by 1 and themselves.
- Prime Factorization of 7: 7 is a prime number, so its prime factorization is simply 7.
- Prime Factorization of 9: 9 = 3 x 3 = 3².
To find the LCM using prime factorization:
- Identify all the prime factors present in either number. In this case, we have 3 and 7.
- For each prime factor, take the highest power present in any of the factorizations. The highest power of 3 is 3² (from 9), and the highest power of 7 is 7¹ (from 7).
- Multiply these highest powers together: 3² x 7 = 9 x 7 = 63.
Therefore, the LCM of 7 and 9, using prime factorization, is 63. This method is generally faster and more efficient than listing multiples, especially for larger numbers with many factors.
Method 3: Using the Formula (LCM and GCD Relationship)
The least common multiple (LCM) and the greatest common divisor (GCD) of two numbers are closely related. The product of the LCM and GCD of two numbers is always equal to the product of the two numbers. This relationship provides another way to find the LCM.
- Find the GCD of 7 and 9: Since 7 and 9 have no common factors other than 1, their greatest common divisor (GCD) is 1.
- Apply the formula: LCM(a, b) = (a x b) / GCD(a, b)
Substituting the values for 7 and 9:
LCM(7, 9) = (7 x 9) / GCD(7, 9) = 63 / 1 = 63.
Therefore, the LCM of 7 and 9 is 63. This method is particularly useful when you already know the GCD of the two numbers, making the calculation even quicker.
Applications of LCM
The LCM has numerous applications across various mathematical fields and real-world scenarios:
-
Adding and Subtracting Fractions: Finding the LCM of the denominators is crucial for adding or subtracting fractions with different denominators. For example, to add 1/7 and 1/9, you'd find the LCM (63) and rewrite the fractions with this common denominator.
-
Scheduling and Cyclical Events: LCM is used in scheduling problems where events repeat at different intervals. For instance, if two buses arrive at a station every 7 and 9 minutes respectively, the LCM will tell you when they'll arrive at the station simultaneously again.
-
Modular Arithmetic: LCM plays a key role in modular arithmetic, which is used in cryptography and computer science.
-
Ratio and Proportion Problems: LCM helps in solving problems involving ratios and proportions where you need to find equivalent ratios with a common multiple.
-
Least Common Denominator (LCD): In fraction arithmetic, the LCM is also known as the least common denominator (LCD). Finding the LCD simplifies fraction operations significantly.
Mathematical Explanation: Why does the Prime Factorization Method Work?
The prime factorization method works because it systematically accounts for all the prime factors present in the numbers. By selecting the highest power of each prime factor, we ensure that the resulting number is divisible by both original numbers. It's a guaranteed way to find the smallest number that satisfies this condition. Every integer can be uniquely expressed as a product of its prime factors (Fundamental Theorem of Arithmetic). The LCM cleverly combines these prime factors to create the smallest number divisible by both inputs.
Frequently Asked Questions (FAQ)
Q1: What is the difference between LCM and GCD?
A1: The least common multiple (LCM) is the smallest number that is a multiple of both numbers, while the greatest common divisor (GCD) is the largest number that divides both numbers without leaving a remainder.
Q2: Can the LCM of two numbers be one of the numbers?
A2: Yes, if one number is a multiple of the other. For example, the LCM of 4 and 8 is 8.
Q3: Is there a formula for finding the LCM of more than two numbers?
A3: Yes, you can extend the prime factorization method or the GCD-based formula to find the LCM of multiple numbers. The prime factorization method involves finding all prime factors and selecting the highest power for each.
Q4: How can I verify if I've correctly calculated the LCM?
A4: Check if the calculated LCM is divisible by both original numbers. If it's not, you've made an error in the calculation. You can also use different methods to cross-check your answer.
Conclusion
Finding the least common multiple (LCM) of 7 and 9, whether through listing multiples, prime factorization, or using the LCM-GCD relationship, consistently yields the answer 63. Understanding the different approaches and the underlying mathematical principles enhances your problem-solving skills. The LCM is not just a mathematical concept but a powerful tool with wide-ranging applications in various fields. Mastering this concept lays a solid foundation for further explorations in mathematics and its practical applications. Remember to choose the method most suitable for the numbers involved; for smaller numbers, listing multiples might suffice, while for larger numbers, prime factorization is significantly more efficient. The understanding of LCM, particularly as demonstrated through the LCM of 7 and 9, provides a strong basis for further mathematical studies and problem-solving.
Latest Posts
Latest Posts
-
Adding And Subtracting Fractions Algebra
Sep 24, 2025
-
Musee Des Beaux Arts Auden
Sep 24, 2025
-
Loretta Young And Clark Gable
Sep 24, 2025
-
6 8 As A Percent
Sep 24, 2025
-
Informal Communication And Formal Communication
Sep 24, 2025
Related Post
Thank you for visiting our website which covers about Lcm Of 7 And 9 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.