Hcf Of 48 And 80
marihuanalabs
Sep 23, 2025 · 6 min read
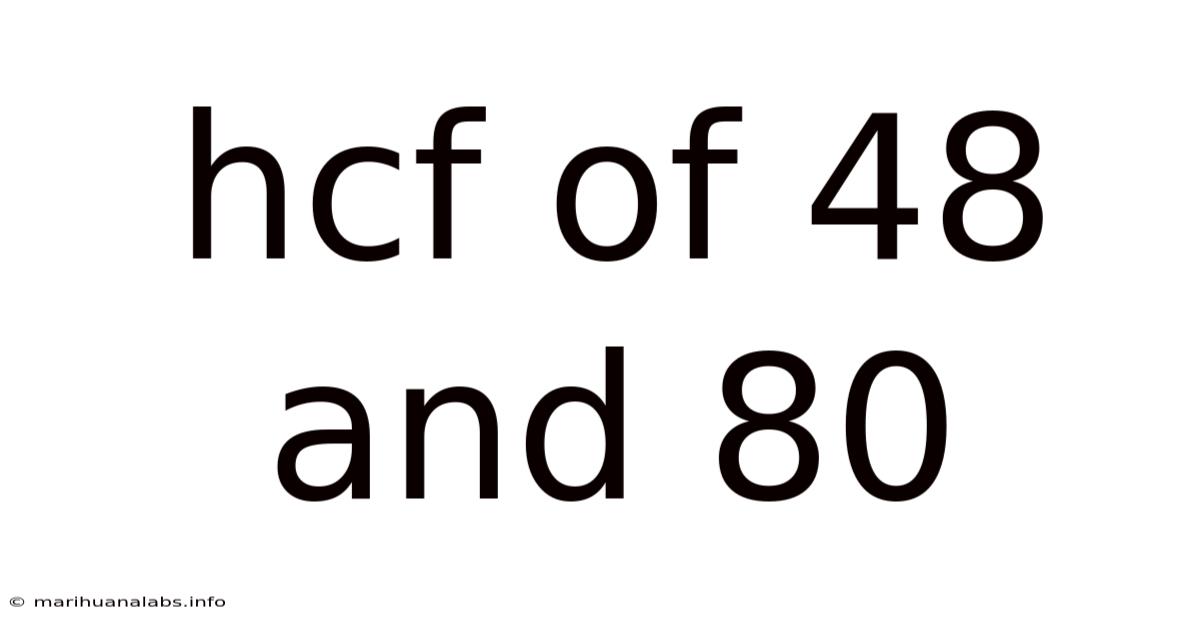
Table of Contents
Finding the Highest Common Factor (HCF) of 48 and 80: A Comprehensive Guide
Understanding the highest common factor (HCF), also known as the greatest common divisor (GCD), is a fundamental concept in mathematics with applications ranging from simplifying fractions to solving complex algebraic problems. This article will delve into the process of finding the HCF of 48 and 80, exploring various methods and providing a comprehensive understanding of the underlying principles. We'll cover everything from basic factorization to more advanced techniques, ensuring you'll grasp this crucial mathematical concept.
Introduction to Highest Common Factor (HCF)
The highest common factor (HCF) of two or more numbers is the largest number that divides each of them without leaving a remainder. In simpler terms, it's the biggest number that's a factor of both numbers. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12. The factors of 18 are 1, 2, 3, 6, 9, and 18. The common factors of 12 and 18 are 1, 2, 3, and 6. The highest of these common factors is 6; therefore, the HCF of 12 and 18 is 6. This article will specifically focus on determining the HCF of 48 and 80, using several different methods.
Method 1: Prime Factorization
This method involves breaking down each number into its prime factors – numbers that are only divisible by 1 and themselves. Let's apply this to 48 and 80:
-
Prime factorization of 48: 48 can be broken down as 2 x 24 = 2 x 2 x 12 = 2 x 2 x 2 x 6 = 2 x 2 x 2 x 2 x 3 = 2<sup>4</sup> x 3
-
Prime factorization of 80: 80 can be broken down as 2 x 40 = 2 x 2 x 20 = 2 x 2 x 2 x 10 = 2 x 2 x 2 x 2 x 5 = 2<sup>4</sup> x 5
Now, we identify the common prime factors and their lowest powers:
Both 48 and 80 share the prime factor 2, and the lowest power of 2 present in both factorizations is 2<sup>4</sup> (or 16). There are no other common prime factors.
Therefore, the HCF of 48 and 80 is 2<sup>4</sup> = 16.
Method 2: Listing Factors
This method is straightforward but can become time-consuming for larger numbers. We list all the factors of each number and then find the largest factor common to both.
-
Factors of 48: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
-
Factors of 80: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
By comparing the lists, we can see that the common factors are 1, 2, 4, 8, and 16. The highest of these common factors is 16. This confirms the result obtained using prime factorization.
Method 3: Euclidean Algorithm
The Euclidean algorithm is an efficient method for finding the HCF of two numbers, especially when dealing with larger numbers. It's based on the principle that the HCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers become equal, and that number is the HCF.
Let's apply the Euclidean algorithm to 48 and 80:
- Start with the larger number (80) and the smaller number (48).
- Divide the larger number by the smaller number and find the remainder: 80 ÷ 48 = 1 with a remainder of 32.
- Replace the larger number with the smaller number (48) and the smaller number with the remainder (32).
- Repeat the process: 48 ÷ 32 = 1 with a remainder of 16.
- Replace the larger number with the smaller number (32) and the smaller number with the remainder (16).
- Repeat the process: 32 ÷ 16 = 2 with a remainder of 0.
- Since the remainder is 0, the HCF is the last non-zero remainder, which is 16.
Understanding the Significance of HCF
The HCF has several important applications in mathematics and other fields:
-
Simplifying Fractions: To simplify a fraction to its lowest terms, we divide both the numerator and the denominator by their HCF. For example, if we have the fraction 48/80, we can simplify it by dividing both by their HCF (16): 48/16 = 3 and 80/16 = 5, so the simplified fraction is 3/5.
-
Solving Word Problems: Many word problems involving division and common factors utilize the concept of HCF. For instance, problems related to dividing objects into equal groups or finding the largest possible size of identical squares that can be cut from a rectangular sheet involve finding the HCF.
-
Algebraic Expressions: The HCF plays a crucial role in simplifying algebraic expressions by factoring out the common factor.
-
Number Theory: The HCF is a fundamental concept in number theory, used in various theorems and proofs.
Frequently Asked Questions (FAQ)
Q: What if the HCF of two numbers is 1?
A: If the HCF of two numbers is 1, it means the numbers are relatively prime or coprime. This signifies that they don't share any common factors other than 1.
Q: Can the HCF of two numbers be larger than either of the numbers?
A: No. The HCF can never be larger than either of the numbers involved because the HCF must be a factor of both numbers.
Q: Which method is the most efficient for finding the HCF?
A: For larger numbers, the Euclidean algorithm is generally the most efficient method because it avoids the need for complete prime factorization or listing all factors. However, for smaller numbers like 48 and 80, all three methods are relatively easy to apply.
Q: Can we find the HCF of more than two numbers?
A: Yes. To find the HCF of more than two numbers, you can use any of the methods described above, but you would apply them iteratively. For example, to find the HCF of three numbers A, B, and C, you would first find the HCF of A and B, and then find the HCF of that result and C.
Conclusion
Finding the highest common factor (HCF) of two numbers is a crucial skill in mathematics. We explored three different methods—prime factorization, listing factors, and the Euclidean algorithm—to determine the HCF of 48 and 80, arriving at the same answer: 16. Understanding these methods and the underlying principles will equip you with the tools to solve a wide range of mathematical problems involving common factors and divisors. The choice of method depends largely on the size of the numbers involved and your personal preference; however, the Euclidean algorithm generally proves the most efficient for larger numbers. Remember, the HCF is more than just a mathematical concept; it's a fundamental building block for understanding more complex mathematical ideas and applications. Mastering the HCF lays a strong foundation for further exploration in algebra, number theory, and various other mathematical fields.
Latest Posts
Latest Posts
-
Squeezing Wrenching Grasping Scraping Clutching
Sep 23, 2025
-
10 Divided By 5 2
Sep 23, 2025
-
77 Degrees Celsius To Fahrenheit
Sep 23, 2025
-
Board Games For One Player
Sep 23, 2025
-
Static Pressure Vs Dynamic Pressure
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about Hcf Of 48 And 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.