10 Divided By 5 2
marihuanalabs
Sep 23, 2025 · 5 min read
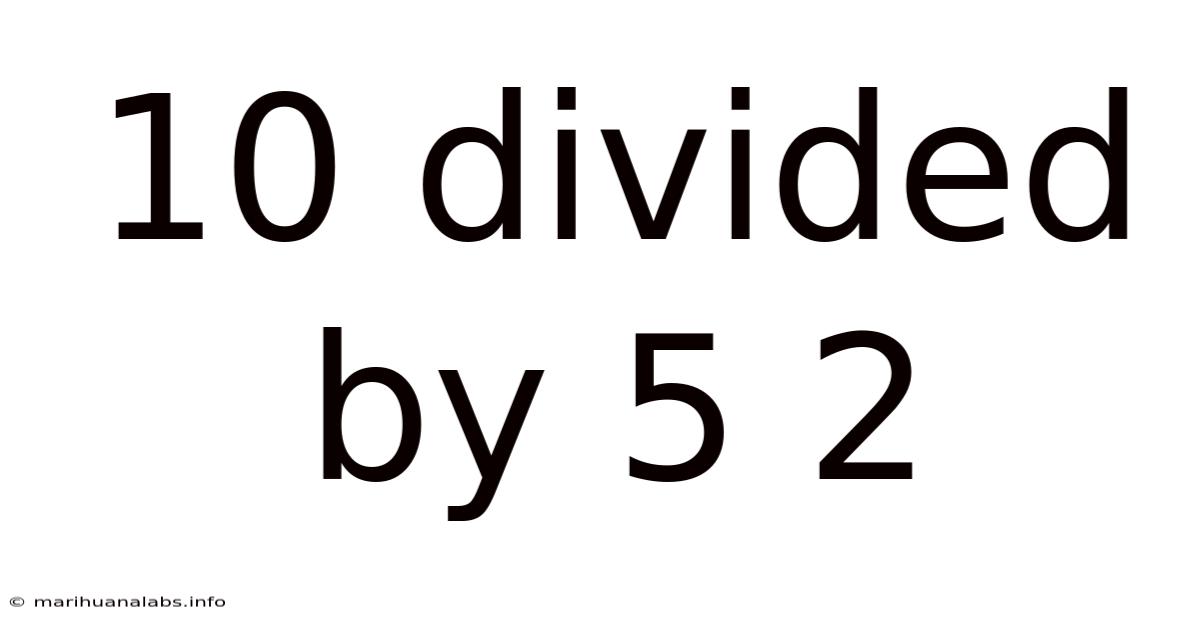
Table of Contents
Decoding the Mystery: A Deep Dive into 10 Divided by 5²
This article explores the seemingly simple mathematical problem of 10 divided by 5², breaking down the process step-by-step and delving into the underlying principles. Understanding this seemingly basic calculation unlocks a deeper comprehension of order of operations, exponents, and division—essential concepts in mathematics. We'll not only solve the problem but also explore its broader implications and address common misconceptions. This detailed explanation ensures a complete understanding, suitable for learners of all levels.
Understanding the Problem: 10 ÷ 5²
The expression "10 divided by 5²" asks us to perform a division operation where 10 is the dividend and 5² is the divisor. The key to solving this accurately lies in understanding the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction). This dictates that exponents are calculated before division.
Step-by-Step Solution
-
Addressing the Exponent: The first step involves evaluating the exponent, 5². This means 5 multiplied by itself: 5 x 5 = 25.
-
Performing the Division: Now that we've simplified the expression, we have 10 ÷ 25. This translates to "how many times does 25 go into 10?"
-
The Result: 25 does not go into 10 a whole number of times. Therefore, the answer is a decimal or fraction. To find the decimal answer, we perform the division: 10 ÷ 25 = 0.4. To express it as a fraction, we simply write it as 10/25, which simplifies to 2/5.
Therefore, the solution to 10 divided by 5² is 0.4 or 2/5.
The Significance of Order of Operations (PEMDAS/BODMAS)
The order of operations is paramount in mathematics. Ignoring PEMDAS (or BODMAS, Brackets, Orders, Division and Multiplication, Addition and Subtraction, which is commonly used in other parts of the world) can lead to incorrect results. In our example, if we divided 10 by 5 before squaring the 5, we would get:
10 ÷ 5 = 2 2² = 4
This is a drastically different, and incorrect, answer. The order of operations ensures consistency and accuracy in mathematical calculations.
Exponents: A Deeper Dive
Exponents, also known as powers or indices, represent repeated multiplication. In the expression 5², the '2' is the exponent, indicating that 5 is multiplied by itself twice. Understanding exponents is crucial for various mathematical concepts, including:
- Algebra: Solving equations and simplifying algebraic expressions often involves working with exponents.
- Geometry: Calculating areas and volumes of shapes frequently requires the use of exponents.
- Calculus: Exponents form the foundation of many calculus concepts, such as derivatives and integrals.
- Scientific Notation: Exponents are used extensively in scientific notation to represent extremely large or small numbers concisely.
For example, 10³ (10 cubed) is 10 x 10 x 10 = 1000. Similarly, 10⁻² (10 to the power of -2) is 1/10² = 1/100 = 0.01. Negative exponents represent reciprocals.
Division: Beyond the Basics
Division, in its simplest form, is the process of splitting a quantity into equal parts. It is the inverse operation of multiplication. While the example above involves simple division, the concept extends to more complex scenarios including:
- Long Division: Used for dividing larger numbers where mental calculation becomes difficult.
- Polynomial Division: Dividing expressions containing variables and exponents.
- Synthetic Division: A shortcut method for polynomial division.
- Division with Decimals and Fractions: Understanding how to divide numbers with decimal points or in fractional form.
Mastering division is fundamental to numerous mathematical applications and problem-solving techniques.
Fractions and Decimals: Interchangeability
Our solution highlighted both decimal (0.4) and fractional (2/5) representations. These are interchangeable and equally valid. Understanding how to convert between fractions and decimals is another crucial skill:
-
Fraction to Decimal: Divide the numerator (top number) by the denominator (bottom number). For example, 2/5 = 2 ÷ 5 = 0.4.
-
Decimal to Fraction: Express the decimal as a fraction with a denominator that is a power of 10 (10, 100, 1000, etc.). Then simplify the fraction. For example, 0.4 = 4/10 = 2/5.
Practical Applications
Understanding the concepts behind 10 ÷ 5² extends far beyond a single mathematical problem. These skills are applied in various fields, including:
- Engineering: Calculating dimensions, material quantities, and forces.
- Finance: Determining interest rates, loan payments, and investment returns.
- Computer Science: Developing algorithms and solving computational problems.
- Physics: Solving equations related to motion, energy, and other physical phenomena.
- Everyday Life: Dividing resources, calculating proportions, and understanding discounts.
Common Misconceptions
A frequent mistake is neglecting the order of operations. Always remember PEMDAS/BODMAS to ensure accuracy. Another common error is incorrectly handling exponents or converting between fractions and decimals. Practice and careful attention to detail are key to avoiding these errors.
Frequently Asked Questions (FAQ)
-
Q: What if the problem was 5² ÷ 10? A: In this case, we would first calculate 5² (25) and then divide by 10, resulting in 25 ÷ 10 = 2.5 or 5/2. The order of operations remains crucial.
-
Q: Can I use a calculator to solve this? A: Yes, absolutely. Calculators are valuable tools for performing calculations, but it's crucial to understand the underlying mathematical principles.
-
Q: Why is understanding the order of operations so important? A: The order of operations ensures that everyone arrives at the same correct answer for a given mathematical expression. Without it, there would be ambiguity and inconsistency.
-
Q: What are some other examples where exponents and division are used together? A: Consider calculating the volume of a cube (side³), or dividing a quantity among multiple people (division), or calculating compound interest where both exponents and division play a crucial role.
Conclusion: Beyond the Numbers
While seemingly simple, the calculation of 10 divided by 5² provides a gateway to understanding fundamental mathematical concepts. By mastering the order of operations, exponents, and division, you build a solid foundation for tackling more complex mathematical problems. The ability to accurately perform these calculations is not just about getting the right answer; it’s about developing critical thinking skills and problem-solving abilities that are applicable across a wide range of disciplines and real-world scenarios. Remember the importance of precision, understanding the underlying principles, and the power of consistent practice.
Latest Posts
Latest Posts
-
Formative Assessment Versus Summative Assessment
Sep 23, 2025
-
We Need New Names Book
Sep 23, 2025
-
Meaning Of Area Of Study
Sep 23, 2025
-
Serial Dilution Biology A Level
Sep 23, 2025
-
4 Kg How Many Grams
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about 10 Divided By 5 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.