8 13 As A Percent
marihuanalabs
Sep 13, 2025 · 5 min read
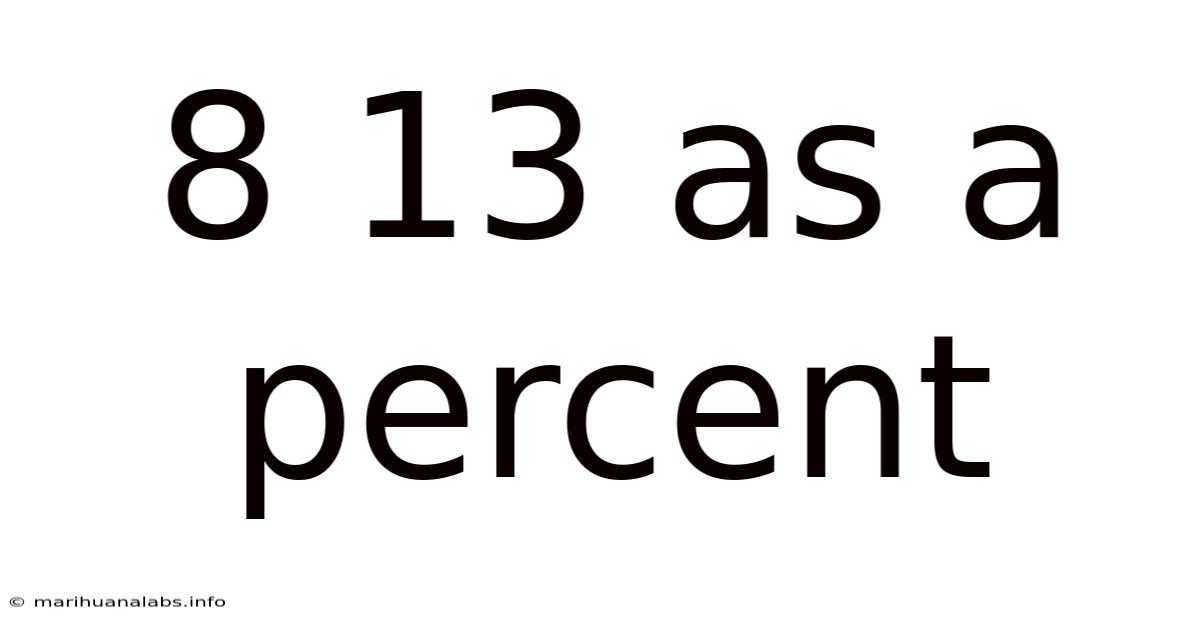
Table of Contents
8/13 as a Percent: A Comprehensive Guide to Fraction-to-Percentage Conversion
Understanding how to convert fractions to percentages is a fundamental skill in mathematics with applications spanning various fields, from finance and statistics to everyday life. This article will delve deep into the process of converting the fraction 8/13 into a percentage, explaining the underlying concepts and providing a thorough understanding of the calculation. We'll explore different methods, address potential difficulties, and answer frequently asked questions to equip you with a comprehensive grasp of this important mathematical operation. This guide will help you confidently tackle similar fraction-to-percentage conversions in the future.
Introduction: Understanding Fractions and Percentages
Before jumping into the conversion of 8/13, let's clarify the basic concepts of fractions and percentages. A fraction represents a part of a whole, expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). For instance, in the fraction 8/13, 8 is the numerator and 13 is the denominator. This means we are considering 8 parts out of a total of 13 parts.
A percentage, on the other hand, expresses a proportion as a fraction of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or 1/2. Converting a fraction to a percentage essentially involves finding the equivalent fraction with a denominator of 100.
Method 1: Direct Conversion using Division
The most straightforward method for converting 8/13 to a percentage involves two simple steps:
-
Divide the numerator by the denominator: Divide 8 by 13. This gives us approximately 0.61538.
-
Multiply the result by 100: Multiply the decimal value obtained in step 1 by 100 to express it as a percentage. 0.61538 x 100 = 61.538%.
Therefore, 8/13 is approximately equal to 61.54% when rounded to two decimal places.
Method 2: Creating an Equivalent Fraction with a Denominator of 100
While the direct division method is efficient, understanding the underlying principle of creating an equivalent fraction with a denominator of 100 provides a deeper conceptual understanding. This method involves finding a number that, when multiplied by the denominator (13), results in 100 (or a close approximation). Unfortunately, there's no whole number that perfectly multiplies 13 to give 100. However, we can use a strategy that allows for a very close approximation:
-
Set up a proportion: We can set up a proportion: 8/13 = x/100, where 'x' represents the numerator we need to find.
-
Solve for x: To solve for x, we can cross-multiply: 13x = 800.
-
Calculate x: Divide both sides by 13: x = 800/13 ≈ 61.538.
-
Express as a percentage: Therefore, x ≈ 61.54%, aligning with the result from the previous method.
Method 3: Using a Calculator
Most scientific and standard calculators have a built-in function to perform this conversion directly. Simply enter the fraction 8/13 and then use the percentage function (%) or convert the resulting decimal to a percentage by multiplying by 100. This method provides a quick and accurate result, especially useful for more complex fractions.
Understanding the Decimal Result: Recurring Decimals
It's important to note that the decimal representation of 8/13 (0.6153846153846...) is a recurring decimal. This means the sequence of digits "615384" repeats infinitely. When converting to a percentage, we must round the decimal to a certain number of decimal places for practical purposes. Rounding to two decimal places, as done previously, gives us 61.54%, providing a sufficiently accurate approximation for most applications.
Practical Applications of Fraction-to-Percentage Conversions
The ability to convert fractions to percentages is essential in many real-world situations:
- Financial calculations: Calculating interest rates, discounts, profit margins, and tax rates often involves converting fractions to percentages.
- Data analysis and statistics: Representing data visually using charts and graphs frequently requires converting fractions or ratios into percentages.
- Scientific experiments and research: Expressing experimental results and probabilities often involves percentages.
- Everyday tasks: Calculating tips in restaurants, determining sale prices, and understanding survey results all involve percentage calculations.
Addressing Potential Difficulties and Common Errors
- Incorrect order of operations: Ensure you divide the numerator by the denominator before multiplying by 100. Reversing the order will lead to an incorrect result.
- Rounding errors: When rounding decimal values, be consistent and aware that rounding can introduce small inaccuracies. The level of precision required depends on the context of the problem.
- Misunderstanding of percentages: Remember that a percentage represents a proportion out of 100. This fundamental concept is crucial for accurately interpreting and using percentages.
Frequently Asked Questions (FAQ)
-
Q: Is 61.54% the exact value of 8/13?
- A: No, 61.54% is an approximation. The exact value of 8/13 as a percentage is a recurring decimal (61.53846153846...). 61.54% is a rounded approximation, sufficient for most practical purposes.
-
Q: Can I use a different denominator besides 100 to convert a fraction to a percentage?
- A: While you can use other denominators, the percentage is ultimately defined as a fraction of 100. Converting to a different denominator requires further steps to then convert that fraction into a percentage. Using 100 simplifies the process.
-
Q: How do I convert a percentage back into a fraction?
- A: To convert a percentage back into a fraction, divide the percentage by 100 and simplify the resulting fraction. For example, 61.54% would be 61.54/100, which simplifies to 3077/5000.
-
Q: What if the fraction is an improper fraction (numerator greater than denominator)?
- A: The process remains the same. Divide the numerator by the denominator, then multiply by 100 to obtain the percentage. The resulting percentage will be greater than 100%.
Conclusion: Mastering Fraction-to-Percentage Conversions
Converting fractions to percentages is a valuable skill with widespread applications. This article has explored three methods for converting 8/13 to a percentage, providing a thorough explanation of the underlying mathematical principles. By understanding these methods, addressing potential difficulties, and utilizing the provided FAQ section, you can confidently perform similar conversions and apply this knowledge to various real-world situations. Remember to choose the method most comfortable for you and to always double-check your work, paying attention to rounding and order of operations. Mastering this skill will undoubtedly enhance your mathematical abilities and improve your problem-solving skills across numerous fields.
Latest Posts
Latest Posts
-
Adjectives That Describe The Moon
Sep 14, 2025
-
And Miles To Go Before
Sep 14, 2025
-
6 Divided By 2 5
Sep 14, 2025
-
Positive Consumption Externality Diagram Explained
Sep 14, 2025
-
Ken Follett The Kingsbridge Novels
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about 8 13 As A Percent . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.