3x X 2 X 2
marihuanalabs
Sep 11, 2025 · 6 min read
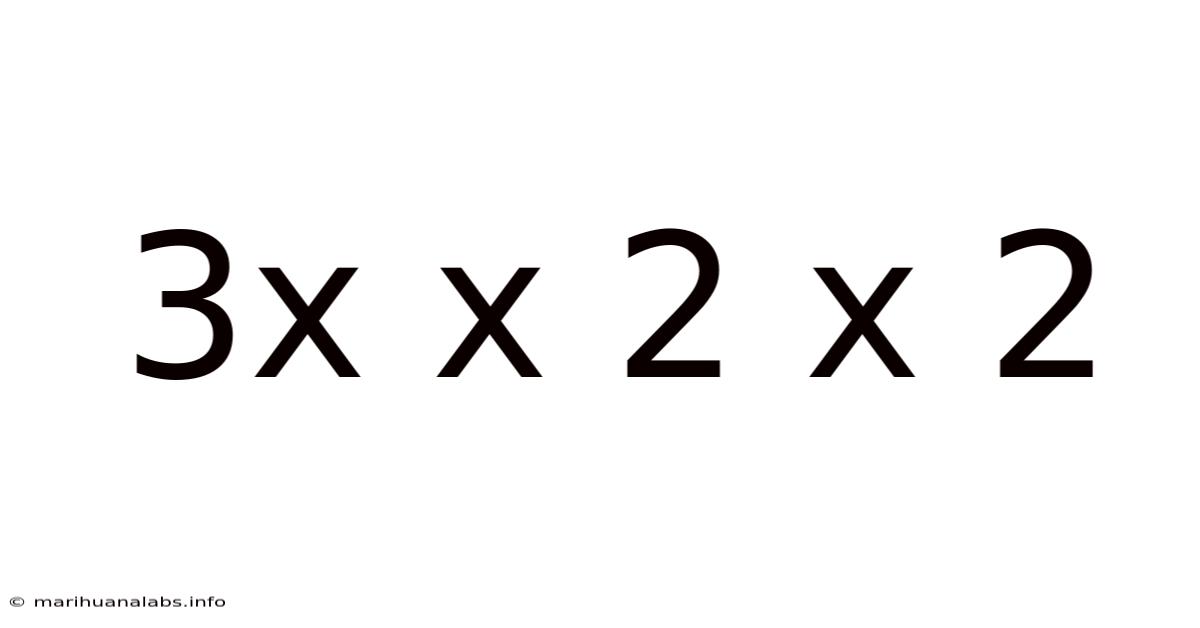
Table of Contents
Decoding 3 x 3 x 2 x 2: A Deep Dive into Multiplication and its Applications
This article explores the seemingly simple mathematical expression "3 x 3 x 2 x 2," unraveling its meaning, demonstrating its calculation, and expanding on its relevance in various fields. We'll move beyond the basic arithmetic to understand the underlying principles of multiplication and its broader applications in real-world scenarios. This exploration will be accessible to a wide audience, from elementary school students grasping multiplication fundamentals to those seeking a deeper understanding of its significance in more complex mathematical concepts.
Understanding the Basics: Multiplication as Repeated Addition
At its core, multiplication is a shortcut for repeated addition. The expression "3 x 3 x 2 x 2" signifies repeated multiplication of these numbers. Let's break it down step-by-step.
-
3 x 3: This represents three groups of three, which can be visualized as three rows of three objects each. Adding them together (3 + 3 + 3) equals 9. Alternatively, we can directly multiply 3 by 3 to get 9.
-
2 x 2: Similar to the above, this represents two groups of two, visually depicted as two rows of two objects each. Adding them (2 + 2) or multiplying them directly gives us 4.
-
Combining the Results: Now, we have the intermediary results: 9 and 4. To complete the expression "3 x 3 x 2 x 2," we multiply these two results: 9 x 4.
-
Final Calculation: 9 x 4 equals 36. Therefore, the solution to 3 x 3 x 2 x 2 is 36.
Different Approaches to Calculation: Order of Operations
While the above method is straightforward, it's important to note the commutative and associative properties of multiplication. These properties allow us to change the order of operations without altering the final result. We could calculate this expression in various ways:
- Method 1 (as shown above): (3 x 3) x (2 x 2) = 9 x 4 = 36
- Method 2: (3 x 2) x (3 x 2) = 6 x 6 = 36
- Method 3: 3 x (3 x 2 x 2) = 3 x 12 = 36
- Method 4: (3 x 3 x 2) x 2 = 18 x 2 = 36
The associative property states that we can group the numbers differently without affecting the product. The commutative property allows us to rearrange the order of the numbers without changing the product. This flexibility is crucial in more complex calculations.
Beyond the Numbers: Real-World Applications
The seemingly simple calculation 3 x 3 x 2 x 2 holds practical significance in numerous situations. Let's explore a few examples:
-
Geometry: Imagine a rectangular prism (a box). If the prism has dimensions of 3 units by 3 units by 2 units, the calculation 3 x 3 x 2 would determine the volume (in cubic units) of the prism's bottom layer. Multiplying this by another 2 (representing two layers) gives the total volume: 3 x 3 x 2 x 2 = 36 cubic units.
-
Combinatorics: Let's say you have 3 shirts, 3 pants, and 2 pairs of shoes. The total number of outfits you can create is 3 x 3 x 2 = 18. If you have two different jackets, you can multiply the total outfits by 2, making it 18 x 2 = 36 different outfit combinations.
-
Area Calculations: Consider a rectangular area divided into smaller squares. If the area consists of 3 rows of 3 squares each (a 3x3 grid) and each of these squares is further divided into 2x2 smaller squares, the total number of smaller squares is 3 x 3 x 2 x 2 = 36.
-
Data Representation: In computer science, data is often stored in arrays or matrices. The expression could represent the size of a 3x3 matrix where each element is further composed of a 2x2 sub-matrix.
-
Everyday Scenarios: Imagine buying 3 boxes of chocolates, each containing 3 rows with 2 chocolates per row and 2 layers of rows. The total number of chocolates you have is 3 x 3 x 2 x 2 = 36.
Expanding the Concept: Exponents and Powers
The expression "3 x 3 x 2 x 2" can be simplified using exponents. Remember that an exponent indicates how many times a base number is multiplied by itself. We can rewrite the expression as:
- 3² x 2² = 9 x 4 = 36
Here, 3² (3 squared) means 3 x 3, and 2² (2 squared) means 2 x 2. Using exponents makes the expression more concise and easier to understand, especially when dealing with larger numbers or more complex calculations.
This leads us into the realm of exponential growth, a concept that appears in various fields such as population growth, compound interest, and radioactive decay.
Connecting to Algebra: Variables and Equations
Introducing variables to the equation elevates our understanding from simple arithmetic to algebra. Instead of fixed numbers, we can use letters to represent unknown quantities. Let's consider a more general equation:
- a x b x c x d = x
Where a, b, c, d represent variables, and x represents the unknown product. This general equation can be used to model numerous real-world scenarios where the specific values of a, b, c, and d might vary. Solving for x requires substituting the actual values for the variables and performing the multiplication.
Frequently Asked Questions (FAQ)
Q1: What if the numbers were different? How would I solve, for example, 4 x 5 x 2 x 1?
A1: The process remains the same. You would multiply the numbers sequentially: 4 x 5 = 20; 20 x 2 = 40; 40 x 1 = 40. The solution is 40.
Q2: Is there a specific order I must follow when multiplying multiple numbers?
A2: While the order doesn't inherently matter due to the commutative and associative properties of multiplication, performing calculations in a logical sequence (e.g., left to right or grouping similar numbers) can enhance efficiency and clarity.
Q3: How can I check my answer to ensure accuracy?
A3: You can use a calculator to verify your answer. You can also work backwards by dividing the final result by one of the original numbers and continuing the division until you arrive at the remaining numbers.
Q4: What are some common mistakes students make when performing multiplication?
A4: Common mistakes include errors in basic multiplication facts, misplacing decimal points (if dealing with decimal numbers), and not following the correct order of operations in more complex expressions.
Conclusion: The Significance of 3 x 3 x 2 x 2 and Beyond
This seemingly simple mathematical expression, 3 x 3 x 2 x 2, serves as a gateway to understanding the power and versatility of multiplication. We've explored its basic calculation, different approaches to solving it, and its diverse applications in various fields. Moving beyond the numerical solution, we've touched upon exponents, algebraic equations, and the importance of understanding fundamental mathematical principles. Remember that mastering these core concepts paves the way for tackling more complex mathematical challenges and understanding the world around us more effectively. The seemingly simple calculation of 36 opens a door to a vast and fascinating world of mathematical possibilities.
Latest Posts
Latest Posts
-
What Is Teacher Performance Assessment
Sep 11, 2025
-
What Does Index Form Mean
Sep 11, 2025
-
To The Lighthouse Plot Summary
Sep 11, 2025
-
What Is 20 Of 180
Sep 11, 2025
-
33 Degrees Celsius To Fahrenheit
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about 3x X 2 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.