What Is 20 Of 180
marihuanalabs
Sep 11, 2025 · 6 min read
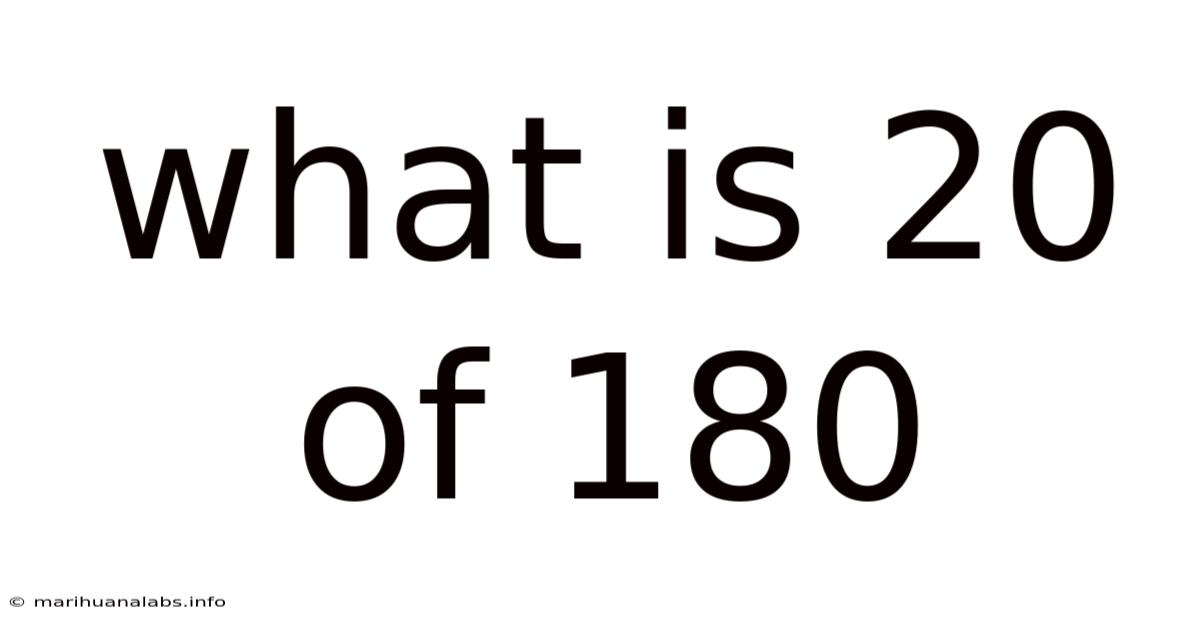
Table of Contents
What is 20 of 180? Understanding Percentages, Fractions, and Ratios
This article will explore the seemingly simple question, "What is 20 of 180?" But we'll delve far beyond a simple calculation. We'll unpack the underlying mathematical concepts, including percentages, fractions, and ratios, illustrating their practical applications and exploring various methods for solving similar problems. This comprehensive guide is designed for anyone, from students needing to brush up on their math skills to adults seeking to improve their everyday numeracy. Understanding these concepts is crucial for various aspects of life, from budgeting and shopping to interpreting data and making informed decisions.
Introduction: Beyond the Simple Calculation
The immediate answer to "What is 20 of 180?" is 20/180. However, this fraction can be simplified and expressed in several ways, each offering a unique insight into the relationship between these two numbers. We will examine these different representations, clarifying the mathematical principles involved and highlighting their practical significance.
Method 1: Using Fractions
The most straightforward approach is to express the problem as a fraction: 20 out of 180 can be written as 20/180. This fraction represents the ratio of 20 to 180. To simplify this fraction, we find the greatest common divisor (GCD) of 20 and 180. The GCD of 20 and 180 is 20. Dividing both the numerator and the denominator by 20, we get:
20/180 = 1/9
This simplified fraction, 1/9, means that 20 represents one-ninth of 180. This is a fundamental way to understand the relationship between the two numbers. This fraction can be further interpreted in terms of percentages and decimals, as we will see below.
Method 2: Calculating Percentages
Percentages provide a common and easily understandable way to express proportions. To calculate the percentage that 20 represents of 180, we use the following formula:
(Part / Whole) * 100%
In this case:
(20 / 180) * 100% = 0.1111... * 100% ≈ 11.11%
Therefore, 20 is approximately 11.11% of 180. The "..." indicates that the decimal 0.1111... is a repeating decimal, meaning the digit 1 continues infinitely. For practical purposes, rounding to two decimal places (11.11%) is sufficient.
Method 3: Using Decimals
Expressing the relationship as a decimal is another useful approach. We simply divide 20 by 180:
20 / 180 = 0.1111...
Again, we encounter the repeating decimal 0.1111... This decimal representation directly shows the proportion of 20 to 180. Multiplying this decimal by 100 gives us the percentage, as shown in Method 2.
Understanding the Concepts: Fractions, Ratios, and Percentages
Let's delve deeper into the core mathematical concepts involved:
-
Fractions: A fraction represents a part of a whole. It's expressed as a numerator (the top number) divided by a denominator (the bottom number). In our example, 20/180, 20 is the part and 180 is the whole.
-
Ratios: A ratio compares two or more quantities. It shows the relative sizes of the quantities. The ratio of 20 to 180 is written as 20:180 or 20/180. Ratios can be simplified, just like fractions, to their simplest form (1:9 in this case).
-
Percentages: A percentage is a fraction expressed as a number out of 100. It's a way to express proportions as a fraction of 100. For instance, 11.11% means 11.11 out of 100.
Practical Applications: Real-World Examples
Understanding these concepts has numerous practical applications in everyday life:
-
Budgeting: Calculating percentages helps in budgeting, such as determining the percentage of income spent on various expenses (housing, food, transportation, etc.).
-
Shopping: Discounts and sales are often expressed as percentages. Understanding percentages helps you calculate the actual price after a discount.
-
Data Analysis: In many fields, data is presented as percentages or proportions. Understanding these concepts helps in interpreting data and making informed decisions.
-
Cooking: Recipes often require adjusting ingredient quantities based on the number of servings. This involves working with proportions and fractions.
Solving Similar Problems: A Step-by-Step Guide
Let's outline a step-by-step approach to solving similar problems:
-
Identify the Part and the Whole: Clearly identify the "part" (the smaller number) and the "whole" (the larger number). In our example, 20 is the part, and 180 is the whole.
-
Express as a Fraction: Write the part as the numerator and the whole as the denominator to create a fraction (Part/Whole).
-
Simplify the Fraction: Simplify the fraction to its lowest terms by finding the greatest common divisor (GCD) of the numerator and the denominator and dividing both by the GCD.
-
Convert to Percentage: Multiply the simplified fraction by 100% to express it as a percentage.
-
Convert to Decimal: Divide the part by the whole to express the proportion as a decimal.
Advanced Concepts: Proportions and Proportionality
The problem "What is 20 of 180?" also touches upon the concept of proportion. A proportion is a statement that two ratios are equal. We can express the relationship between 20 and 180 as a proportion:
20/180 = x/100 (where x represents the percentage)
Solving for x, we get:
x = (20/180) * 100 = 11.11%
This illustrates how proportions are used to solve problems involving ratios and percentages.
Frequently Asked Questions (FAQ)
-
What if the numbers are larger or more complex? The same principles apply. Use a calculator to aid in the calculations, but the steps remain the same: form a fraction, simplify, convert to percentage, and convert to decimal.
-
Can I use a calculator for this? Absolutely! Calculators are useful for simplifying fractions and performing calculations, especially with larger numbers.
-
What if the problem involves three or more numbers? While the basic principle of finding the ratio remains the same, the calculation will be slightly more complex. Focus on identifying the relationships between the different numbers.
-
What are some real-world applications beyond those mentioned? Understanding proportions and percentages is crucial in finance (interest rates, investment returns), science (data analysis, experimental results), and engineering (scaling, measurements).
Conclusion: Mastering the Fundamentals
The seemingly simple question, "What is 20 of 180?" provides a valuable opportunity to review and reinforce fundamental mathematical concepts. By understanding fractions, ratios, percentages, and decimals, we gain the tools to solve a wide variety of problems encountered in daily life and various professional settings. Mastering these skills builds a strong foundation for more advanced mathematical concepts and enhances our ability to interpret and utilize numerical information effectively. Remember to practice regularly to solidify your understanding and build confidence in your mathematical abilities. The more you practice, the easier and more intuitive these concepts will become. Don't hesitate to work through similar problems using different numbers to further cement your understanding and develop your problem-solving skills.
Latest Posts
Latest Posts
-
How Many Inches In 56cm
Sep 11, 2025
-
Multiply Whole Numbers And Decimals
Sep 11, 2025
-
I Am Sorry In German
Sep 11, 2025
-
What Is A Ground Bass
Sep 11, 2025
-
Ode To A Nightingale Analysis
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 180 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.