1 Million Divided By 12
marihuanalabs
Sep 08, 2025 · 5 min read
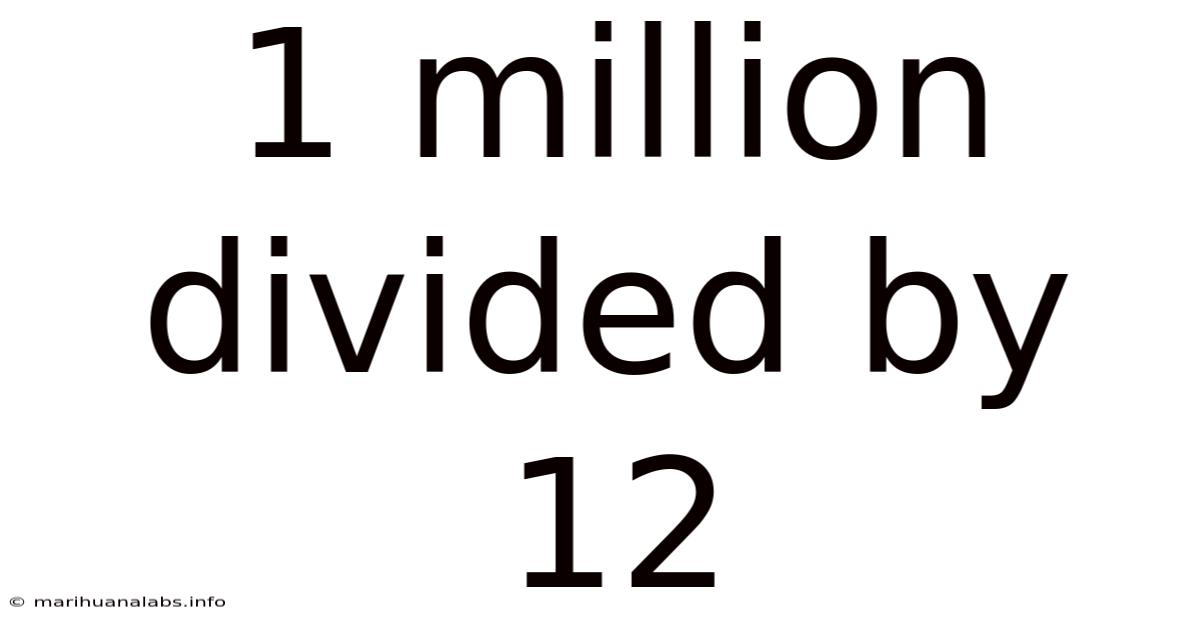
Table of Contents
One Million Divided by Twelve: A Deep Dive into Division and its Applications
Introduction: Ever wondered what happens when you divide a million by twelve? This seemingly simple arithmetic problem opens a door to a deeper understanding of division, its practical applications, and even some fascinating connections to other areas of mathematics. This comprehensive guide will not only provide the answer but also explore the process, related concepts, and real-world scenarios where this type of calculation is relevant. We'll delve into the methods for solving this problem, discuss the significance of the result, and address frequently asked questions.
Understanding the Problem: 1,000,000 ÷ 12
The core question is straightforward: how many times does 12 fit into 1,000,000? This is a classic division problem. While a calculator readily provides the answer, understanding the underlying process is crucial for grasping the broader mathematical concepts involved. This understanding extends beyond simple arithmetic and touches upon topics like fractions, decimals, and even estimation techniques.
Methods for Solving 1,000,000 ÷ 12
Several methods can be employed to solve this division problem, each offering a unique approach and level of understanding:
-
Long Division: This traditional method involves a step-by-step process of dividing, multiplying, subtracting, and bringing down digits. While potentially lengthy for large numbers like 1,000,000, it provides a solid foundation in understanding the division algorithm.
-
Calculator: The simplest method is using a calculator. This instantly provides the answer, but it lacks the pedagogical value of the other methods. Nevertheless, calculators are indispensable tools for checking answers and solving more complex problems.
-
Repeated Subtraction: Imagine repeatedly subtracting 12 from 1,000,000 until you reach zero. The number of times you subtract represents the answer. While impractical for this specific problem due to the magnitude of the numbers, this method clearly illustrates the fundamental concept of division as repeated subtraction.
-
Breaking Down the Problem: We can simplify the problem by breaking it into smaller, more manageable parts. For instance, we can divide 1,000,000 by 10 (resulting in 100,000) and then divide that result by 1.2 (which is 12/10). This approach requires more steps but can be less daunting than tackling the entire problem at once. This method cleverly utilizes the properties of multiplication and division, showcasing their interconnectedness.
The Solution and its Interpretation
Using any of the methods above (and most conveniently, a calculator), we find that 1,000,000 divided by 12 equals 83,333.333...
This result is a decimal number with a repeating decimal part (.333...). The repeating decimal signifies that the division does not result in a whole number. This is because 1,000,000 is not perfectly divisible by 12. The remainder is not zero. In fact, the remainder is 4.
The answer can be expressed as both a decimal and a fraction:
- Decimal: 83,333.333...
- Fraction: 83,333 + 1/3 or 250,000/3
Understanding this recurring decimal is crucial. It highlights the limitations of representing certain divisions with whole numbers.
Real-World Applications
The seemingly abstract problem of dividing 1,000,000 by 12 has several practical applications across various fields:
-
Finance: Imagine distributing $1,000,000 equally among 12 individuals. Each person would receive $83,333.33. The remaining cents would need to be handled appropriately, perhaps rounding up or down depending on the context.
-
Manufacturing: If a factory produces 1,000,000 units of a product per year and works 12 months, the average monthly production is 83,333.33 units. Again, handling the fractional unit requires consideration of production realities.
-
Resource Allocation: Distributing resources such as water, land, or even time equally among 12 projects or teams with a total of 1,000,000 units to allocate would yield the same result.
-
Data Analysis: In analyzing large datasets, dividing a total value (1,000,000) by the number of data points (12) could provide average values.
These examples demonstrate that division is a fundamental operation for fair distribution, resource management, and data analysis, applicable across numerous fields. The result, even with its repeating decimal, carries real-world significance.
Exploring Related Concepts
Solving 1,000,000 ÷ 12 leads to a deeper understanding of several related mathematical concepts:
-
Divisibility Rules: While 1,000,000 is not divisible by 12, understanding divisibility rules helps to predict whether a number is divisible by another without actually performing the division. Divisibility rules can simplify the process of determining divisibility for smaller numbers. For 12, a number is divisible by 12 if it's divisible by both 3 and 4.
-
Factors and Multiples: Exploring the factors of 1,000,000 and the multiples of 12 provides insights into the relationship between these numbers.
-
Fractions and Decimals: The result's decimal representation highlights the connection between fractions and decimals. The repeating decimal (.333...) represents the fractional part 1/3.
-
Remainders: The remainder after the division (4 in this case) is crucial and signifies the portion of 1,000,000 that is "left over" after the equal distribution.
Frequently Asked Questions (FAQ)
-
Q: Why is the answer a repeating decimal?
- A: Because 1,000,000 is not perfectly divisible by 12. The division results in a fraction that cannot be expressed as a terminating decimal.
-
Q: How can I handle the remainder in real-world applications?
- A: The handling of the remainder depends on the context. You might round up or down, distribute the remainder proportionally, or account for it in other ways.
-
Q: Are there other ways to solve this problem without a calculator?
- A: Yes, long division and breaking down the problem into smaller parts are viable alternatives.
-
Q: What are the practical implications of the repeating decimal?
- A: In practical situations, you would often round the result to a suitable number of decimal places depending on the required level of accuracy.
Conclusion:
Dividing 1,000,000 by 12, while seemingly straightforward, reveals a wealth of mathematical concepts and practical applications. The result, 83,333.333..., with its repeating decimal, highlights the interplay between whole numbers, fractions, and decimals. Understanding the process and its implications is far more valuable than simply obtaining the answer. This problem serves as a springboard for exploring deeper mathematical principles and their relevance in various fields, from finance and manufacturing to resource allocation and data analysis. The seemingly simple arithmetic problem becomes a powerful tool for demonstrating core mathematical concepts and their application in the real world. Remember that the essence of mathematical understanding lies not just in the answer but in the journey to arrive at it and the broader implications it unveils.
Latest Posts
Latest Posts
-
Fun Facts About Henry Viii
Sep 08, 2025
-
Books By Frances Hodgson Burnett
Sep 08, 2025
-
What Is A Framework Story
Sep 08, 2025
-
2x X 2x X 2x
Sep 08, 2025
-
Span Of Control Business Definition
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 1 Million Divided By 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.