2x X 2x X 2x
marihuanalabs
Sep 08, 2025 · 6 min read
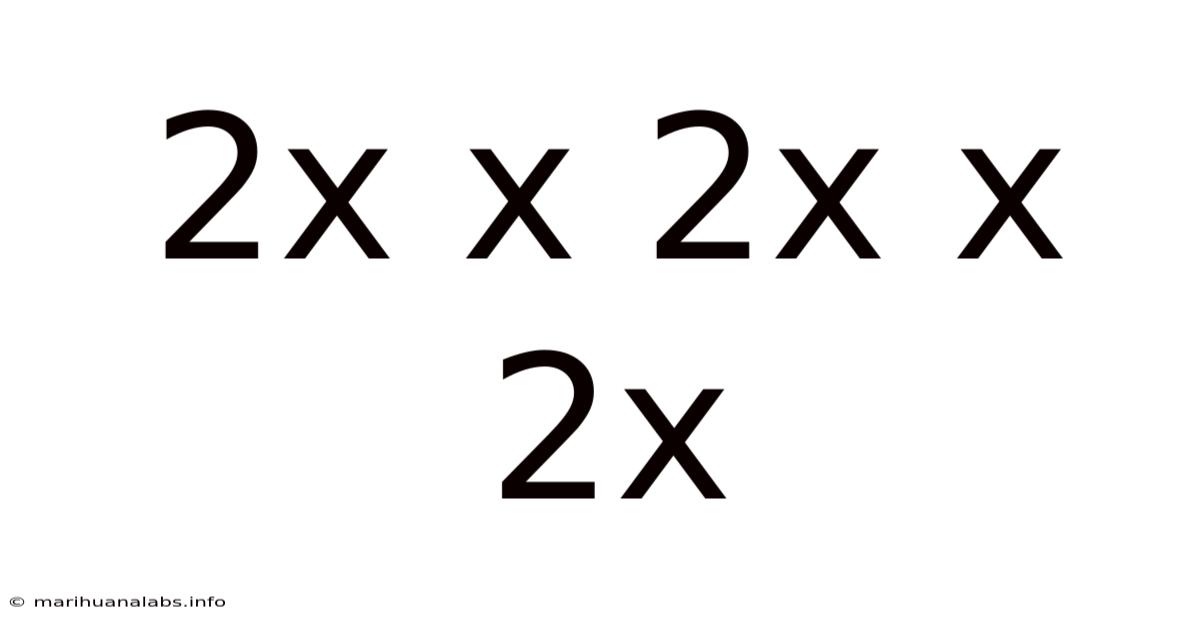
Table of Contents
Decoding the Mystery: Exploring the Multiplicative Power of 2x x 2x x 2x
This article delves into the mathematical concept represented by the expression "2x x 2x x 2x," exploring its implications across various fields, from simple arithmetic to advanced calculus and its applications in real-world scenarios. Understanding this seemingly simple expression unlocks a deeper understanding of exponential growth, scaling, and the power of compounding. We will unpack this concept systematically, addressing potential confusions and highlighting its practical significance.
Introduction: Unveiling the Power of Repeated Multiplication
The expression "2x x 2x x 2x" represents repeated multiplication. It's a fundamental concept in algebra and forms the basis for understanding exponential functions. While seemingly straightforward, its implications extend far beyond basic arithmetic. This exploration will cover the simplification of the expression, its graphical representation, and the diverse contexts where it finds application. We'll also address common misconceptions and answer frequently asked questions. Understanding this expression is key to comprehending various mathematical concepts and their real-world applications, from calculating compound interest to modeling population growth.
Simplifying the Expression: From Multiplication to Exponentiation
The core of understanding "2x x 2x x 2x" lies in its simplification. Recall that multiplication is repeated addition, and exponentiation is repeated multiplication. Let's break it down step-by-step:
-
Identify the repeated factor: The expression contains the factor "2x" three times.
-
Rewrite using exponential notation: This repeated multiplication can be concisely expressed using exponents. The expression becomes (2x)³.
-
Expanding the expression: To fully understand the result, we can expand the expression using the rules of exponents: (2x)³ = 2³ x x³ = 8x³.
Therefore, "2x x 2x x 2x" simplifies to 8x³. This simplified form is much easier to work with in further calculations and analyses.
Graphical Representation and Visualizing Growth
The function y = 8x³ represents a cubic function. Cubic functions are characterized by their S-shaped curves. Graphing this function provides a visual representation of the exponential growth implied by the original expression.
-
The x-intercept: The graph intersects the x-axis at x = 0, indicating that when x is zero, y is also zero.
-
The y-intercept: The graph does not intersect the y-axis at any point other than the origin (0,0).
-
Asymptotes: A cubic function does not have horizontal or vertical asymptotes.
-
Growth Rate: The growth rate of the function is significantly accelerated as x increases. This demonstrates the rapid expansion inherent in the original expression "2x x 2x x 2x," highlighting the power of repeated multiplication. A small change in x leads to a disproportionately large change in y.
By visualizing the graph of y = 8x³, we gain a clearer understanding of the rapid growth associated with the expression.
Applications in Real-World Scenarios
The principles illustrated by "2x x 2x x 2x" have wide-ranging applications across various fields:
-
Compound Interest: Compound interest calculations rely on the principle of repeated multiplication. If you invest a principal amount (x) with an interest rate of 200% per period, compounded over three periods, the final amount would be calculated similarly to our expression, resulting in 8x.
-
Population Growth: In biological systems, population growth can often be modeled using exponential functions. If a population doubles (2x) in size over three successive periods, the final population size will be 8x, mirroring the result of our simplified expression.
-
Volume Calculations: The expression could represent the volume of a cube where each side is 2x units long. The volume would be (2x)³, or 8x³.
-
Computer Science: In algorithms and data structures, the time complexity of certain operations can be expressed using exponential functions, directly related to the concept of repeated multiplication, impacting efficiency.
-
Physics and Engineering: Many physical phenomena exhibit exponential growth or decay, which can be modeled using functions similar to the simplified expression.
These examples demonstrate the broad applicability of the mathematical principle encapsulated by "2x x 2x x 2x," highlighting its relevance across various disciplines.
Expanding the Concept: Generalizing the Expression
The expression can be generalized to understand the broader principle of exponential growth. The pattern can be extended:
- (2x)⁴ = 16x⁴
- (2x)⁵ = 32x⁵
- (2x)^n = 2^n x^n
This demonstrates the general formula for repeated multiplication of a term by itself n times. This understanding is critical for grasping more complex mathematical concepts.
Addressing Common Misconceptions
Several misconceptions can arise when dealing with this type of expression:
-
Incorrect Order of Operations: It's crucial to understand that the exponent applies to the entire term (2x), not just the 2. Failing to account for this will lead to an incorrect answer.
-
Confusing Multiplication and Addition: The expression involves repeated multiplication, not addition. Conflating these operations will result in a drastically different outcome.
-
Misinterpreting Exponential Growth: The rapid growth associated with exponential functions can be counterintuitive. It's important to appreciate the significant difference between linear and exponential growth.
Addressing these misconceptions is crucial for a proper understanding of the concept.
Frequently Asked Questions (FAQ)
-
What if the expression was 2x + 2x + 2x? This would be simple addition, resulting in 6x, significantly different from the exponential result of 8x³.
-
Can this concept be applied to negative values of x? Yes, the expression can be evaluated for negative values of x, but the result will also be negative. The absolute value of the result would still reflect the exponential growth.
-
How does this relate to logarithmic functions? Logarithmic functions are the inverse of exponential functions. They provide a means to solve for x when given the value of y in an equation like y = 8x³.
-
What are the limitations of this model? Exponential growth models often break down in the real world due to limitations like resource scarcity, competition, or external factors not considered in the simplified model.
These FAQs provide further clarity and address potential questions regarding the expression and its implications.
Conclusion: The Enduring Power of Repeated Multiplication
The seemingly simple expression "2x x 2x x 2x," when fully understood, reveals the profound power of repeated multiplication. Simplifying it to 8x³ unlocks its applications across numerous fields. From understanding financial growth to modeling biological phenomena, mastering this concept forms a fundamental building block for tackling more complex mathematical challenges. The visual representation and understanding of the associated exponential growth provide a deeper insight into the dynamics of repeated multiplication and its significant impact across various scientific and practical domains. By mastering this concept, you’ll not only improve your mathematical skills, but also enhance your ability to analyze and interpret growth patterns in the real world. The journey from "2x x 2x x 2x" to 8x³ is more than just a mathematical simplification; it's a doorway to a broader understanding of the world around us.
Latest Posts
Latest Posts
-
200 Degrees Celsius To F
Sep 08, 2025
-
The Raven Himself Is Hoarse
Sep 08, 2025
-
Paris Quotes Romeo And Juliet
Sep 08, 2025
-
Exact Value Of Cos 60
Sep 08, 2025
-
What Is Mild Learning Disability
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about 2x X 2x X 2x . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.