1 Divided By 3 5
marihuanalabs
Sep 09, 2025 · 5 min read
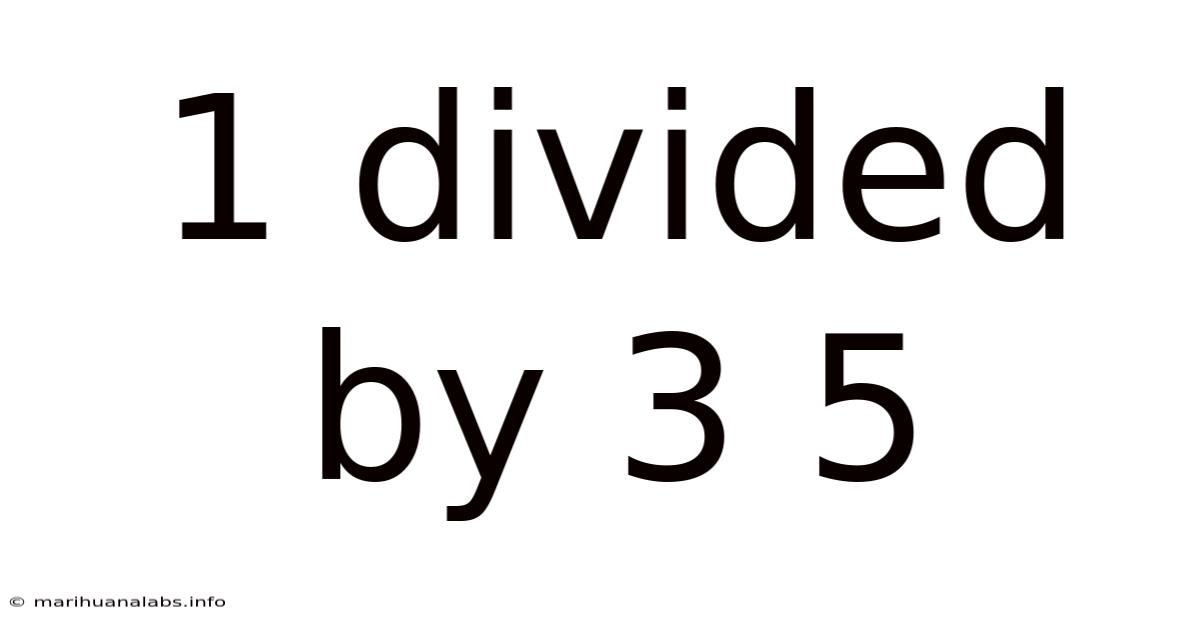
Table of Contents
Decoding 1 Divided by 3.5: A Deep Dive into Division and Decimal Operations
Understanding how to divide 1 by 3.5 might seem straightforward at first glance, but this seemingly simple calculation offers a window into fundamental mathematical concepts like decimal division, fractions, and reciprocal relationships. This article will guide you through the process, explaining the steps involved, providing the scientific rationale behind the method, and answering frequently asked questions to solidify your understanding. We'll explore different approaches to solving this problem, ensuring a comprehensive grasp of the underlying principles.
Introduction: Why 1 ÷ 3.5 Matters
The seemingly simple division problem, 1 divided by 3.5 (or 1 ÷ 3.5), provides a valuable opportunity to reinforce key mathematical skills. It allows us to explore the mechanics of dividing by decimal numbers, convert decimals into fractions for easier calculation, and understand the concept of reciprocals. Mastering this calculation is crucial for a strong foundation in arithmetic, which is essential for more advanced mathematical concepts encountered in algebra, calculus, and beyond. Understanding this process is not just about getting the right answer; it's about building a deeper intuition for how numbers interact.
Method 1: Long Division with Decimals
The most direct approach is using long division. However, dividing by a decimal requires a preliminary step to simplify the process.
-
Convert the divisor to a whole number: To make the long division easier, we multiply both the dividend (1) and the divisor (3.5) by 10. This shifts the decimal point one place to the right in both numbers, resulting in 10 ÷ 35.
-
Perform long division: Now, we perform the long division as we would with whole numbers.
0.2857... 35 | 10.0000 -70 300 -280 200 -175 250 -245 50 -
Interpret the result: The division results in a repeating decimal, 0.285714285714… This can be represented as 0.2̅8̅5̅7̅1̅4̅. The "…" indicates that the sequence 285714 repeats infinitely.
Method 2: Converting to Fractions
This method provides a more elegant and potentially simpler solution, especially if you're comfortable working with fractions.
-
Express 3.5 as a fraction: 3.5 can be written as the improper fraction 7/2.
-
Rewrite the division as a multiplication of reciprocals: Dividing by a fraction is the same as multiplying by its reciprocal. The reciprocal of 7/2 is 2/7. Therefore, 1 ÷ 3.5 becomes 1 × (2/7).
-
Perform the multiplication: Multiplying 1 by 2/7 gives us 2/7.
-
Convert to decimal (optional): To obtain the decimal representation, divide the numerator (2) by the denominator (7) using long division or a calculator. This again yields the repeating decimal 0.285714285714… or 0.2̅8̅5̅7̅1̅4̅.
Method 3: Using a Calculator
The simplest way to solve 1 ÷ 3.5 is by using a calculator. Simply enter "1 ÷ 3.5" and press the equals button. The calculator will directly provide the decimal approximation, which will likely display a truncated version of the repeating decimal, such as 0.285714. Keep in mind that even a calculator provides an approximation; the true value is the infinitely repeating decimal.
The Scientific Rationale: Decimals, Fractions, and Reciprocals
The different methods employed above all rely on fundamental mathematical principles. Let's examine the core concepts:
-
Decimal Numbers: Decimal numbers are a way of representing numbers that are not whole numbers. They use a base-10 system, with a decimal point separating the whole number part from the fractional part.
-
Fractions: Fractions represent parts of a whole. They consist of a numerator (the top number) and a denominator (the bottom number). The denominator indicates how many equal parts the whole is divided into, and the numerator shows how many of those parts are being considered.
-
Reciprocals: The reciprocal of a number is 1 divided by that number. For example, the reciprocal of 5 is 1/5, and the reciprocal of 7/2 is 2/7. Multiplying a number by its reciprocal always results in 1. This principle is fundamental to solving division problems involving fractions.
Understanding Repeating Decimals
The result of 1 ÷ 3.5, 0.2̅8̅5̅7̅1̅4̅, is a repeating decimal. This means that a sequence of digits repeats infinitely. This occurs when the denominator of a fraction (in this case, 7) does not have only 2 and 5 as its prime factors. Such repeating decimals can be expressed using a bar over the repeating sequence.
Frequently Asked Questions (FAQ)
-
Q: Why is the result a repeating decimal? A: The result is a repeating decimal because the fraction 2/7, which is equivalent to 1/3.5, has a denominator (7) that is not a factor of any power of 10 (10, 100, 1000, etc.). When you try to express 2/7 as a decimal, the division process never terminates.
-
Q: How many decimal places should I use? A: The number of decimal places you use depends on the context. For most practical purposes, a few decimal places (e.g., 0.2857) will provide sufficient accuracy. However, for precise mathematical calculations, you should either keep the fraction (2/7) or acknowledge that it's an infinitely repeating decimal.
-
Q: Can I use a calculator for all division problems? A: While calculators are convenient tools, it's crucial to understand the underlying mathematical principles. Calculators are helpful for obtaining approximations, but they may not always reveal the underlying mathematical structure or the nature of repeating decimals.
-
Q: What if the dividend wasn't 1? A: If the dividend were a different number, you would follow the same procedure. For example, to calculate 5 ÷ 3.5, you could convert 3.5 to 7/2, find the reciprocal (2/7), and then multiply 5 by 2/7, resulting in 10/7. You could then convert this fraction into a decimal using long division.
Conclusion: Mastering Division and Beyond
Mastering the division of 1 by 3.5, or any decimal division problem, is about more than just getting the right answer; it's about solidifying your understanding of fundamental mathematical concepts. By exploring different methods, understanding the properties of decimals and fractions, and grasping the concept of reciprocals, you build a strong foundation for tackling more complex mathematical challenges. This seemingly simple problem lays the groundwork for success in more advanced mathematical studies, reinforcing a vital skill set applicable to various fields. The ability to perform such calculations accurately and confidently builds mathematical literacy and fluency. Remember to choose the method most comfortable for you, but always strive to understand the rationale behind each step.
Latest Posts
Latest Posts
-
Animal Farm Ch 1 Summary
Sep 10, 2025
-
Dash Dash Dash Dot Dot
Sep 10, 2025
-
Conjugation Of The Verb Comer
Sep 10, 2025
-
How Much Is Half Litre
Sep 10, 2025
-
Derivative Of X 2 Lnx
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about 1 Divided By 3 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.