Derivative Of X 2 Lnx
marihuanalabs
Sep 10, 2025 · 6 min read
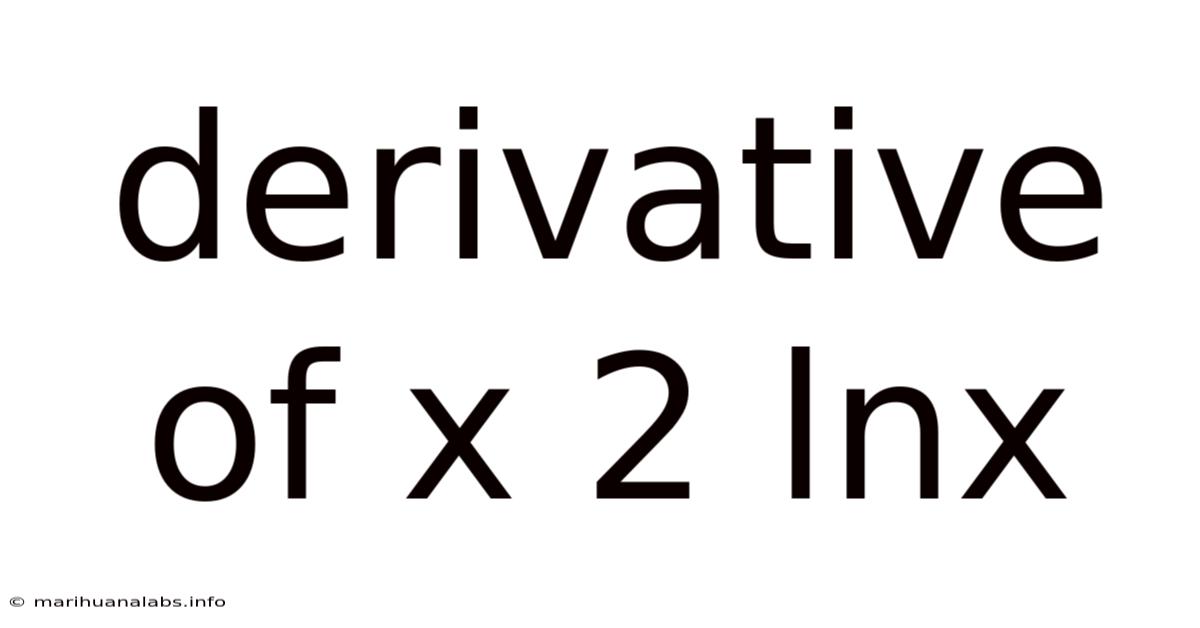
Table of Contents
Decoding the Derivative of x²lnx: A Comprehensive Guide
Finding the derivative of x²lnx might seem daunting at first, especially if you're new to calculus. However, with a systematic approach and a solid understanding of derivative rules, this seemingly complex problem becomes manageable. This article will guide you through the process, explaining each step in detail, addressing common pitfalls, and exploring the broader implications of this derivative. We'll delve into the underlying principles, provide a step-by-step solution, and even answer frequently asked questions. By the end, you'll not only understand how to find the derivative of x²lnx but also gain a deeper appreciation for the power of calculus.
Understanding the Fundamentals: Derivatives and Their Rules
Before tackling the derivative of x²lnx, let's refresh our understanding of derivatives and the key rules we'll be applying. The derivative of a function, denoted as f'(x) or df/dx, represents the instantaneous rate of change of that function with respect to its input variable (x). It essentially tells us how much the function's output changes for an infinitesimally small change in its input.
Several crucial rules govern the calculation of derivatives:
-
Power Rule: The derivative of xⁿ is nxⁿ⁻¹, where n is a constant. For example, the derivative of x³ is 3x².
-
Product Rule: The derivative of a product of two functions, u(x)v(x), is given by u'(x)v(x) + u(x)v'(x). This rule is crucial when dealing with functions that are multiplied together.
-
Constant Multiple Rule: The derivative of a constant multiplied by a function, cf(x), where c is a constant, is simply c * f'(x).
-
Derivative of lnx: The derivative of the natural logarithm function, lnx, is 1/x.
These rules form the foundation for calculating many derivatives, including the one we're focusing on.
Step-by-Step Solution: Deriving x²lnx
Now, let's tackle the derivative of x²lnx. Since we have a product of two functions – x² and lnx – we must employ the product rule.
1. Identify the Functions:
Let u(x) = x² and v(x) = lnx.
2. Find the Derivatives of u(x) and v(x):
- u'(x) = d(x²)/dx = 2x (using the power rule)
- v'(x) = d(lnx)/dx = 1/x (derivative of lnx)
3. Apply the Product Rule:
The product rule states that the derivative of u(x)v(x) is u'(x)v(x) + u(x)v'(x). Substituting our values:
d(x²lnx)/dx = (2x)(lnx) + (x²)(1/x)
4. Simplify the Expression:
We can simplify the expression obtained in the previous step:
d(x²lnx)/dx = 2xlnx + x
Therefore, the derivative of x²lnx is 2xlnx + x.
Exploring the Result: Implications and Interpretations
The derivative we derived, 2xlnx + x, provides valuable insights into the behavior of the original function, x²lnx. Let's explore some key interpretations:
-
Instantaneous Rate of Change: At any given point x, the derivative 2xlnx + x represents the instantaneous rate at which the function x²lnx is changing. For example, if x = 1, the instantaneous rate of change is 2(1)ln(1) + 1 = 1. This means that at x = 1, the function is increasing at a rate of 1 unit per unit change in x.
-
Increasing or Decreasing Function: The sign of the derivative indicates whether the original function is increasing or decreasing. If the derivative is positive, the function is increasing; if it's negative, the function is decreasing. In the case of 2xlnx + x, the sign depends on the value of x. For x > 1/e (approximately 0.368), the derivative is positive, indicating that the function is increasing. For 0 < x < 1/e, the derivative is negative, indicating a decreasing function. At x = 1/e, the derivative is 0, indicating a potential local minimum or maximum.
-
Critical Points: The points where the derivative equals zero (2xlnx + x = 0) are called critical points. These points represent potential local maxima or minima of the function. Solving the equation 2xlnx + x = 0, we find x = 1/e is the only critical point.
Extending the Understanding: Higher-Order Derivatives
We can also explore higher-order derivatives of x²lnx. The second derivative, denoted as f''(x) or d²f/dx², represents the rate of change of the first derivative. To find the second derivative, we simply differentiate the first derivative:
f'(x) = 2xlnx + x
f''(x) = d(2xlnx + x)/dx
Applying the product rule and the derivative of lnx again:
f''(x) = 2(lnx + x(1/x)) + 1
Simplifying:
f''(x) = 2lnx + 3
The second derivative provides information about the concavity of the original function. A positive second derivative indicates that the function is concave up (shaped like a U), while a negative second derivative indicates that it's concave down (shaped like an inverted U).
Advanced Applications and Real-World Examples
Understanding the derivative of x²lnx extends beyond theoretical exercises. It finds applications in various fields, including:
-
Optimization Problems: In engineering and economics, finding the maximum or minimum values of a function is critical. The derivative helps identify critical points that can be further analyzed to determine optimal solutions. The function x²lnx, for example, might model a profit function where x represents the number of units produced. Finding its maximum would help determine the optimal production level to maximize profit.
-
Modeling Natural Phenomena: Functions involving logarithmic terms frequently arise in natural sciences, representing phenomena such as population growth, radioactive decay, or the spread of diseases. The derivative allows for analyzing the rate of change in these processes.
-
Curve Sketching: The first and second derivatives are invaluable tools for accurately sketching the graph of a function. They reveal information about the function's increasing/decreasing intervals, concavity, and the location of critical points.
Frequently Asked Questions (FAQ)
Q1: Why is the product rule necessary for this derivative?
A1: The product rule is essential because the function x²lnx is a product of two functions: x² and lnx. We cannot simply differentiate each term individually; we need the product rule to account for the interaction between these two functions.
Q2: Can I use the quotient rule instead of the product rule?
A2: No, the quotient rule applies to functions in the form u(x)/v(x), not u(x)v(x). The function x²lnx is a product, not a quotient, so the product rule is the correct approach.
Q3: What happens if x is negative?
A3: The natural logarithm function, lnx, is only defined for positive values of x. Therefore, the function x²lnx and its derivative are only defined for x > 0.
Conclusion: Mastering the Derivative and Beyond
This comprehensive guide has explored the derivation of the derivative of x²lnx, providing a detailed step-by-step solution, interpretations of the results, and a glimpse into its broader applications. Mastering this seemingly complex calculation empowers you with a deeper understanding of calculus and its practical uses. Remember, the key to success lies in a firm grasp of the fundamental rules of differentiation—the power rule, the product rule, and the derivative of the natural logarithm. By combining these tools strategically, you can tackle a vast array of derivative problems with confidence. This knowledge forms a crucial foundation for more advanced calculus concepts and their myriad applications across various scientific and engineering disciplines. Continue practicing, explore different functions, and challenge yourself—the rewards of mastering calculus are significant and far-reaching.
Latest Posts
Latest Posts
-
What Is A Sculpture Gallery
Sep 10, 2025
-
Angular Impulse And Angular Momentum
Sep 10, 2025
-
5 Yards How Many Meters
Sep 10, 2025
-
97 7 Degrees Fahrenheit To Celsius
Sep 10, 2025
-
Loveliest Trees The Cherry Now
Sep 10, 2025
Related Post
Thank you for visiting our website which covers about Derivative Of X 2 Lnx . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.