X Squared Times X Squared
marihuanalabs
Sep 05, 2025 · 5 min read
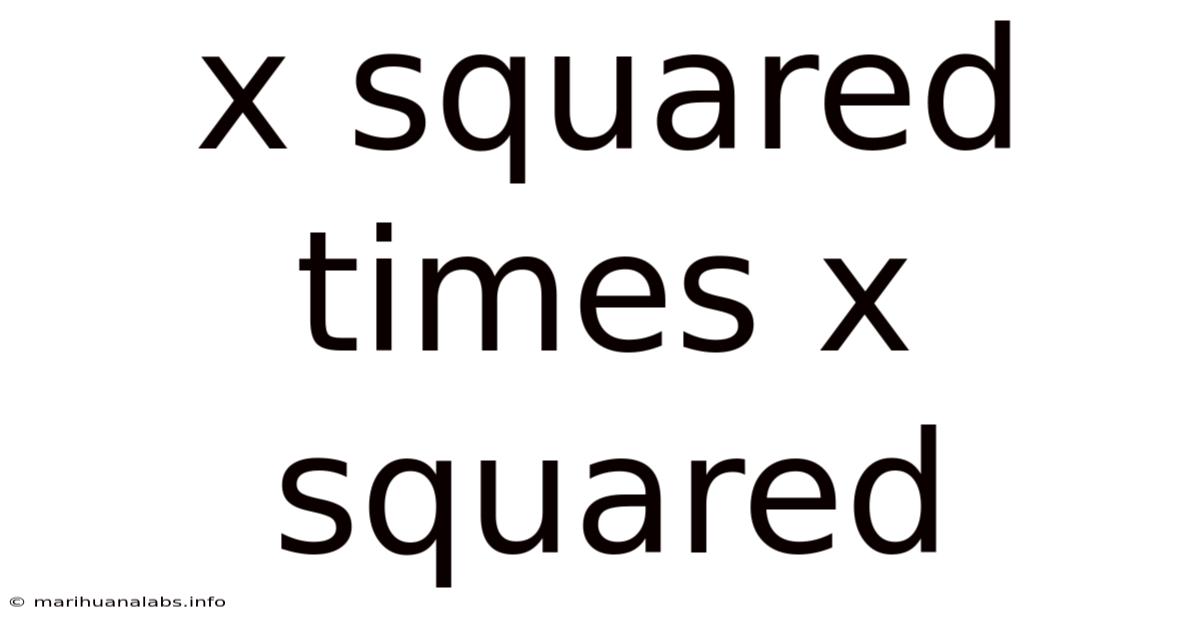
Table of Contents
Understanding x² * x²: A Deep Dive into Exponential Rules
This article explores the fundamental mathematical concept of multiplying exponential expressions, specifically focusing on x² * x². We will delve into the underlying principles, demonstrate the solution, and expand upon the broader applications of exponential rules in algebra and beyond. Understanding this seemingly simple equation unlocks a gateway to more complex algebraic manipulations and a deeper appreciation of mathematical principles. This comprehensive guide will equip you with the knowledge to confidently solve similar problems and build a strong foundation in algebra.
Introduction: The Basics of Exponents
Before diving into x² * x², let's establish a solid understanding of exponents. An exponent, also known as a power or index, indicates how many times a base number is multiplied by itself. For example, in the expression x², 'x' is the base, and '2' is the exponent. This means x² is equivalent to x * x. Similarly, x³ (x cubed) is x * x * x, and so on. Understanding this fundamental concept is crucial for mastering exponential operations.
Solving x² * x²: A Step-by-Step Approach
The multiplication of x² * x² can be solved using the fundamental rules of exponents. The key principle to remember is that when multiplying terms with the same base, you add the exponents.
Step 1: Identify the Base and Exponents
In the expression x² * x², the base is 'x' and the exponent in both terms is '2'.
Step 2: Apply the Rule for Multiplying Exponents with the Same Base
As mentioned earlier, when multiplying exponential terms with the same base, we add the exponents. Therefore:
x² * x² = x⁽²⁺²⁾ = x⁴
Step 3: Simplify the Expression
The simplified form of x² * x² is x⁴. This means x multiplied by itself four times (x * x * x * x).
Therefore, the solution to x² * x² is x⁴.
A Deeper Look: The Mathematical Rationale
The reason we add the exponents when multiplying terms with the same base can be illustrated using the definition of exponents:
x² * x² = (x * x) * (x * x)
Notice that we have four 'x's multiplied together. This is equivalent to x⁴. This demonstrates the fundamental rule: when multiplying terms with the same base, add the exponents. This rule is a cornerstone of algebraic manipulation and is frequently applied in various mathematical contexts.
Expanding on Exponential Rules: Beyond x² * x²
The principle of adding exponents when multiplying terms with the same base extends beyond the simple case of x² * x². Consider these examples:
- x³ * x⁵ = x⁸: (3 + 5 = 8)
- y⁴ * y² * y = y⁷: (4 + 2 + 1 = 7) Remember that y is equivalent to y¹.
- 2² * 2³ = 2⁵ = 32: This works with numerical bases as well.
- (2x)² * (3x)³ = 4x² * 27x³ = 108x⁵: Here, we apply the power of a product rule (discussed below) and then the rule for adding exponents with the same base.
These examples illustrate the versatility and widespread application of this fundamental exponential rule.
Other Relevant Exponential Rules
To fully grasp exponential operations, it's helpful to understand other key rules:
- Power of a Product Rule: (xy)ⁿ = xⁿyⁿ. When raising a product to a power, raise each factor to that power.
- Power of a Quotient Rule: (x/y)ⁿ = xⁿ/yⁿ (where y ≠ 0). When raising a quotient to a power, raise both the numerator and denominator to that power.
- Power of a Power Rule: (xⁿ)ᵐ = xⁿᵐ. When raising a power to a power, multiply the exponents.
- Dividing Exponents with the Same Base: xⁿ / xᵐ = xⁿ⁻ᵐ (where x ≠ 0). When dividing exponential terms with the same base, subtract the exponents.
Practical Applications of Exponential Rules
Exponential rules aren't just abstract mathematical concepts; they have wide-ranging applications in various fields, including:
- Science: Exponential functions model many natural phenomena, such as population growth, radioactive decay, and compound interest.
- Engineering: Exponential calculations are crucial in designing structures, analyzing circuits, and modeling various systems.
- Finance: Compound interest calculations, which are fundamental to investment and loan calculations, rely heavily on exponential functions.
- Computer Science: Exponential growth and decay are relevant to algorithm efficiency and data structure analysis.
Addressing Common Misconceptions
A common mistake is to multiply the exponents when multiplying terms with the same base. Remember, the correct procedure is to add the exponents, not multiply them. This is a fundamental distinction.
Another misconception involves applying the rules inconsistently. Always ensure that you are applying the appropriate rule based on whether you are multiplying, dividing, or raising to a power.
Frequently Asked Questions (FAQ)
Q1: What happens if the bases are different?
A1: If the bases are different (e.g., x² * y³), you cannot simply add the exponents. The expression remains as x² * y³. You can only add exponents when the bases are identical.
Q2: Can I apply these rules to negative exponents?
A2: Yes, the rules apply to negative exponents as well. For example, x⁻² * x³ = x¹. Remember that x⁻ⁿ = 1/xⁿ.
Q3: What if the exponent is zero?
A3: Any non-zero number raised to the power of zero is equal to 1 (x⁰ = 1, where x ≠ 0).
Q4: How can I visualize these concepts?
A4: Visualizing the multiplication of terms with the same base as repeated multiplication can be helpful. For instance, x² * x³ represents (xx) * (xx*x), which is clearly x⁵. Using visual aids or real-world examples can reinforce understanding.
Conclusion: Mastering Exponential Rules
Understanding the multiplication of exponential expressions, as exemplified by x² * x², forms a crucial foundation in algebra and numerous related fields. By mastering the fundamental rule of adding exponents when multiplying terms with the same base, and by understanding the associated rules for other exponential operations, you unlock a powerful toolset for solving a wide range of mathematical problems. This knowledge empowers you to approach more complex mathematical concepts with confidence and clarity. Remember to practice regularly to solidify your understanding and build your problem-solving skills. Continued practice and application of these principles will further enhance your comprehension and fluency in algebra and related mathematical domains. This will enable you to tackle progressively challenging problems with ease and proficiency.
Latest Posts
Latest Posts
-
Map Of The River Seine
Sep 05, 2025
-
Voltage In Series Parallel Circuit
Sep 05, 2025
-
Words That Rhyme With 5
Sep 05, 2025
-
List Of All Percussion Instruments
Sep 05, 2025
-
History Of An Atom Timeline
Sep 05, 2025
Related Post
Thank you for visiting our website which covers about X Squared Times X Squared . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.