X 2 Times X 2
marihuanalabs
Sep 22, 2025 · 5 min read
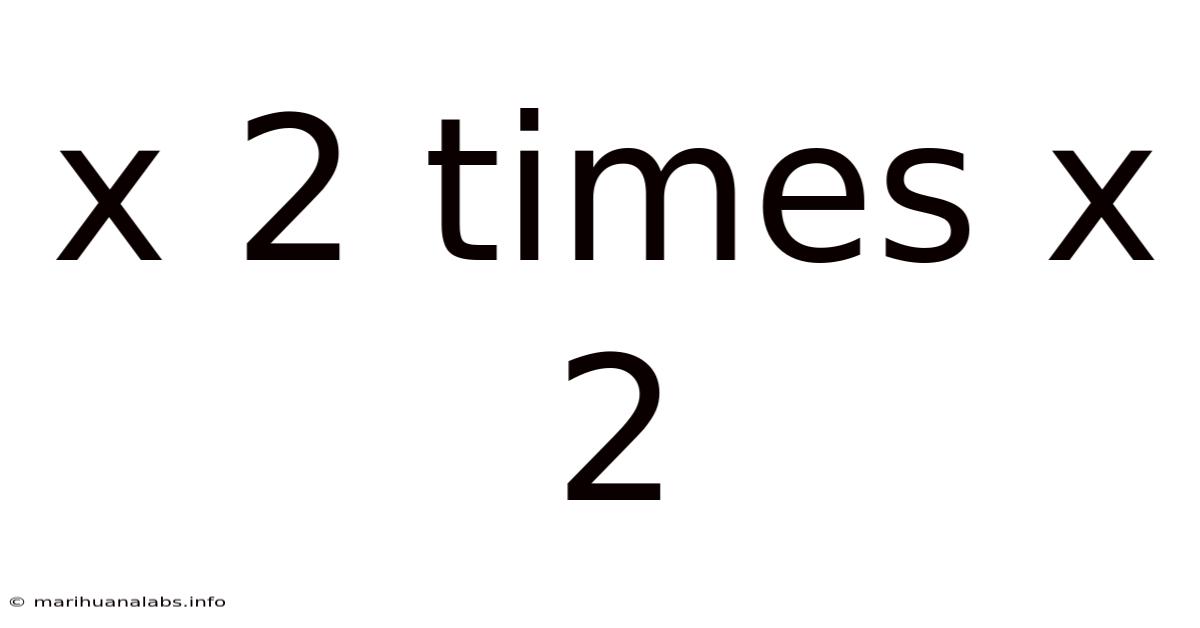
Table of Contents
Exploring the Mathematical Concept: x Multiplied by 2, Then Multiplied by 2 Again (x * 2 * 2)
This article delves into the seemingly simple mathematical expression "x multiplied by 2, then multiplied by 2 again," or more concisely, x * 2 * 2. While the calculation itself is straightforward, understanding its underlying principles and exploring its applications across various mathematical contexts reveals a rich tapestry of concepts applicable to algebra, geometry, and beyond. We'll explore this seemingly simple equation, uncovering its hidden depths and practical significance. Understanding this basic operation forms a crucial foundation for more advanced mathematical studies.
Introduction: The Building Blocks of Mathematics
At its core, x * 2 * 2 represents a fundamental operation in mathematics: multiplication. It's a building block upon which more complex equations and formulas are constructed. The variable 'x' represents an unknown quantity or a placeholder for a number. The expression shows a sequential multiplication: first, 'x' is multiplied by 2, and then the result is multiplied by 2 again. This seemingly simple process underlies numerous concepts in various branches of mathematics and has practical implications in numerous real-world scenarios.
Understanding the Calculation: Step-by-Step Breakdown
Let's break down the calculation step-by-step:
-
x * 2: This step involves multiplying the unknown value 'x' by 2. The result is 2x. This represents a doubling of the initial value. For example, if x = 5, then 5 * 2 = 10.
-
(x * 2) * 2: The result from the first step, 2x, is then multiplied by 2 again. This simplifies to 4x. This further doubles the value obtained in the first step. Using our previous example where x = 5, (5 * 2) * 2 = 10 * 2 = 20.
Simplifying the Expression: The Power of Algebra
Algebra provides a powerful tool to simplify this expression. Notice that multiplying by 2 and then multiplying by 2 again is equivalent to multiplying by 4. Therefore, x * 2 * 2 can be simplified to 4x. This simplified form is more efficient and easier to work with in more complex equations. This simplification demonstrates the power of algebraic manipulation to streamline calculations.
Geometric Interpretation: Visualizing Multiplication
The expression x * 2 * 2 can also be visualized geometrically. Imagine a square with sides of length 'x'. Multiplying by 2 doubles the length of one side, creating a rectangle with sides of length 2x and x. Multiplying by 2 again doubles the other side, resulting in a larger square with sides of length 2x. The area of this larger square is (2x) * (2x) = 4x². While this doesn't directly equate to 4x, it demonstrates how the repeated doubling affects the dimensions and area of a geometric shape. The connection between algebraic expressions and geometric representations is fundamental to understanding mathematical relationships.
Applications in Real-World Scenarios:
The concept of x * 2 * 2 finds applications in various real-world scenarios:
-
Doubling and Redoubling: Imagine a population of bacteria that doubles every hour. If the initial population is 'x', after one hour it becomes 2x, and after two hours it becomes (2x) * 2 = 4x. This simple formula models exponential growth, a crucial concept in biology, finance, and other fields.
-
Scaling and Resizing: In design and engineering, scaling involves enlarging or reducing the size of an object. If an object has a dimension of 'x', and it's scaled up by a factor of 2 twice, the final dimension becomes 4x. This principle applies to blueprints, architectural plans, and image editing.
-
Compound Interest: In finance, compound interest involves earning interest on both the principal amount and accumulated interest. While the formula for compound interest is more complex, the concept of repeated doubling is fundamental to understanding how interest accumulates over time.
-
Programming and Algorithms: In computer programming, this operation can be found within loops and iterative algorithms where a value is repeatedly multiplied. Understanding this basic principle is essential for writing efficient and effective code.
Advanced Applications and Extensions:
The concept of repeated multiplication extends beyond the simple x * 2 * 2 example. Consider the expression x * n * n, where 'n' is any number. This represents multiplying 'x' by 'n' twice. This more generalized expression allows for exploration of a wider range of scenarios involving repeated multiplication.
Furthermore, the concept can be extended to higher powers. The expression x * 2 * 2 is equivalent to 4x, which can also be expressed as 2²x. This introduces the concept of exponents, where the number 2 is raised to the power of 2. This opens up the world of exponential functions and their significant applications in various fields.
Frequently Asked Questions (FAQ)
-
What if x is a negative number? The calculation remains the same. A negative number multiplied by 2 twice still results in a negative number multiplied by 4. For example, if x = -3, then (-3) * 2 * 2 = -12.
-
Can x be a fraction or a decimal? Yes, x can represent any real number, including fractions and decimals. The rules of multiplication apply equally to all real numbers.
-
How does this relate to other mathematical concepts? This simple expression forms a foundation for understanding more complex concepts such as exponents, polynomial expressions, and functions.
-
What are some real-world examples beyond those mentioned? This concept can be applied to recipes (doubling a recipe twice), calculating distances (doubling a distance twice), or any scenario involving repeated doubling.
Conclusion: The Significance of Simplicity
While the expression x * 2 * 2 appears simple on the surface, its underlying principles are fundamental to a deeper understanding of mathematics. From its algebraic simplification to its geometric interpretation and its various real-world applications, this seemingly trivial calculation provides a solid foundation for more advanced mathematical exploration. The ability to manipulate and understand simple expressions like this is a crucial skill for anyone pursuing further studies in mathematics, science, engineering, or any field that requires quantitative reasoning. Mastering this simple concept unlocks the door to a wealth of knowledge and problem-solving capabilities. The seemingly straightforward nature of x * 2 * 2 belies its importance as a building block in the vast and fascinating world of mathematics.
Latest Posts
Latest Posts
-
A B C Murders Cast
Sep 22, 2025
-
Adjectives With The Letter C
Sep 22, 2025
-
Jekyll And Hyde Quote Analysis
Sep 22, 2025
-
Is Poland In The Balkans
Sep 22, 2025
-
Come Here In French Language
Sep 22, 2025
Related Post
Thank you for visiting our website which covers about X 2 Times X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.