X 2 3x 2 0
marihuanalabs
Sep 19, 2025 · 6 min read
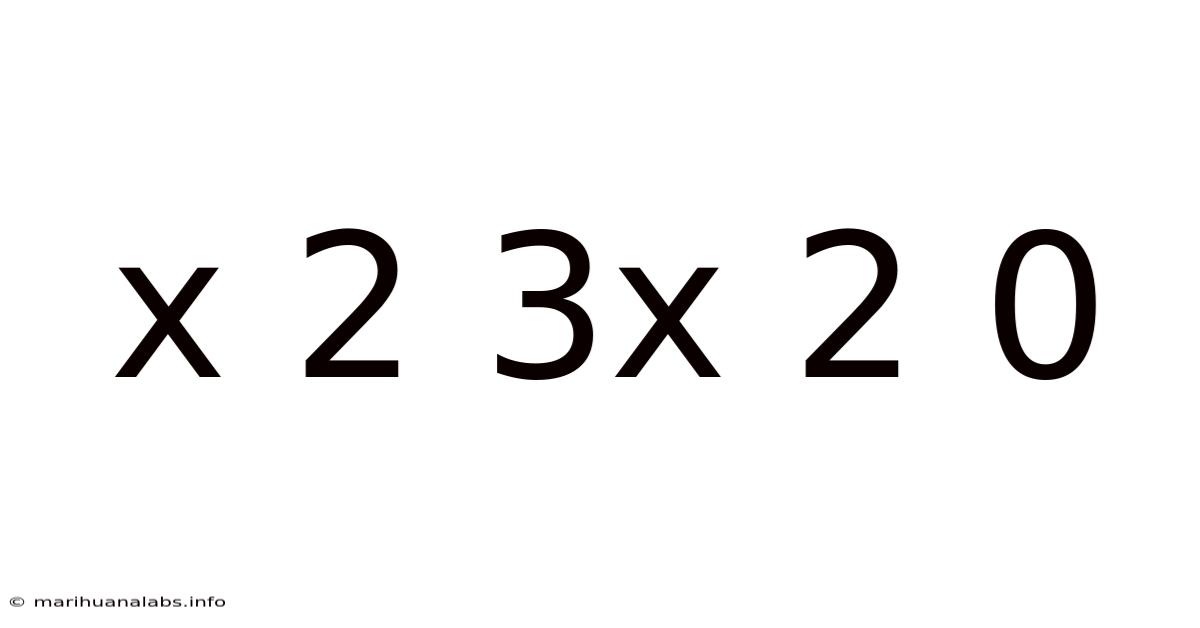
Table of Contents
Solving the Quadratic Equation: x² + 3x² + 2 = 0
This article explores the solution to the equation x² + 3x² + 2 = 0, guiding you through the steps involved in solving quadratic equations and offering a deeper understanding of the underlying mathematical concepts. We'll cover the simplification of the equation, the application of the quadratic formula, and the interpretation of the results. This comprehensive guide is suitable for students learning algebra and anyone wishing to refresh their knowledge of quadratic equations. Understanding quadratic equations is crucial for various fields, from physics and engineering to finance and computer science.
Introduction: Understanding Quadratic Equations
A quadratic equation is a polynomial equation of the second degree, meaning the highest power of the variable (usually x) is 2. The general form of a quadratic equation is ax² + bx + c = 0, where a, b, and c are constants, and a is not equal to zero. Our specific equation, x² + 3x² + 2 = 0, is a simplified form of a quadratic equation.
Before diving into the solution, let's simplify the given equation:
x² + 3x² + 2 = 0
Combining like terms, we get:
4x² + 2 = 0
This simplified equation is now in a form that we can readily solve using various methods.
Method 1: Solving by Rearrangement and Square Roots
This method is particularly useful when the quadratic equation lacks a linear term (bx). Let's solve our simplified equation (4x² + 2 = 0) using this method:
-
Isolate the x² term: Subtract 2 from both sides of the equation:
4x² = -2
-
Solve for x²: Divide both sides by 4:
x² = -1/2
-
Take the square root: Taking the square root of both sides introduces both positive and negative solutions:
x = ±√(-1/2)
Since the square root of a negative number involves imaginary numbers, we can express the solution using the imaginary unit i, where i² = -1:
x = ±√(1/2) * i or x = ±(√2/2)i
Therefore, the solutions to the equation 4x² + 2 = 0 are x = (√2/2)i and x = -(√2/2)i. These are complex conjugate solutions.
Method 2: The Quadratic Formula
The quadratic formula is a powerful tool for solving any quadratic equation, regardless of whether it has real or complex roots. The formula is derived from completing the square and provides a direct method to find the solutions. For a general quadratic equation ax² + bx + c = 0, the quadratic formula is:
x = [-b ± √(b² - 4ac)] / 2a
Let's apply this to our simplified equation, 4x² + 2 = 0. Here, a = 4, b = 0, and c = 2. Substituting these values into the quadratic formula:
x = [-0 ± √(0² - 4 * 4 * 2)] / (2 * 4)
x = ± √(-32) / 8
Again, we encounter a negative number under the square root, indicating complex solutions. Simplifying further:
x = ± √(32)i / 8 = ± √(16 * 2)i / 8 = ± 4√2i / 8 = ± (√2/2)i
This confirms the same solutions we obtained using the rearrangement method: x = (√2/2)i and x = -(√2/2)i.
Understanding Complex Numbers
The solutions we obtained are complex numbers. A complex number is a number that can be expressed in the form a + bi, where 'a' is the real part and 'b' is the imaginary part, and i is the imaginary unit (√-1). In our case, a = 0 and b = ±(√2/2).
Complex numbers are essential in various branches of mathematics, physics, and engineering. They are particularly useful in representing oscillatory phenomena and solving equations that lack real solutions.
Graphical Representation
While we can't directly plot complex solutions on a standard Cartesian coordinate system (which represents real numbers), we can visualize them using a complex plane. The complex plane uses two axes: the real axis (horizontal) and the imaginary axis (vertical). Each complex number is represented as a point on this plane. Our solutions, (√2/2)i and -(√2/2)i, would be plotted on the imaginary axis, symmetrically positioned about the origin.
The Discriminant and Nature of Roots
The expression inside the square root in the quadratic formula, b² - 4ac, is called the discriminant. The discriminant determines the nature of the roots of the quadratic equation:
- b² - 4ac > 0: The equation has two distinct real roots.
- b² - 4ac = 0: The equation has one real root (a repeated root).
- b² - 4ac < 0: The equation has two complex conjugate roots (as in our case).
In our equation, 4x² + 2 = 0, the discriminant is 0² - 4 * 4 * 2 = -32, which is less than 0, hence the two complex conjugate roots.
Further Exploration: Applications of Quadratic Equations
Quadratic equations have a wide range of applications in various fields:
- Physics: Calculating projectile motion, determining the trajectory of objects under the influence of gravity.
- Engineering: Designing structures, analyzing circuits, and solving problems in mechanics.
- Economics and Finance: Modeling growth and decay, calculating interest rates, and optimizing investment strategies.
- Computer Graphics: Creating curves and shapes, used extensively in computer-aided design (CAD) software.
Frequently Asked Questions (FAQ)
Q: Why do we get imaginary solutions in this case?
A: We get imaginary solutions because the discriminant (b² - 4ac) is negative. This indicates that the parabola represented by the quadratic equation does not intersect the x-axis (where y=0). The solutions lie in the complex plane.
Q: What does it mean for two solutions to be complex conjugates?
A: Complex conjugate numbers are pairs of complex numbers that have the same real part but opposite imaginary parts. For example, a + bi and a - bi are complex conjugates. In quadratic equations with real coefficients, complex roots always appear as conjugate pairs.
Q: Can we solve quadratic equations using other methods besides the quadratic formula and rearrangement?
A: Yes, other methods include factoring, completing the square, and graphical methods. The choice of method depends on the specific form of the quadratic equation and personal preference. Factoring is often the quickest method if the equation is easily factorable. Completing the square is a fundamental technique used in deriving the quadratic formula.
Conclusion
Solving the equation x² + 3x² + 2 = 0 involves simplifying the equation to 4x² + 2 = 0 and then employing either the rearrangement method or the quadratic formula. Both methods yield the same complex conjugate solutions: x = (√2/2)i and x = -(√2/2)i. Understanding the concept of the discriminant helps predict the nature of the roots (real or complex). Quadratic equations are fundamental to many areas of mathematics and its applications in science and engineering, highlighting the importance of mastering their solution techniques. This article has provided a comprehensive guide to solving this specific quadratic equation and has explored the underlying mathematical concepts involved, equipping you with a deeper understanding of quadratic equations and their diverse applications.
Latest Posts
Latest Posts
-
How To Reference A Movie
Sep 19, 2025
-
Mega Electron Volts To Joules
Sep 19, 2025
-
English Curriculum For Year 7
Sep 19, 2025
-
How Many Weeks Till September
Sep 19, 2025
-
Geometric Average Vs Arithmetic Average
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about X 2 3x 2 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.