X 2 3 3x 2
marihuanalabs
Sep 14, 2025 · 6 min read
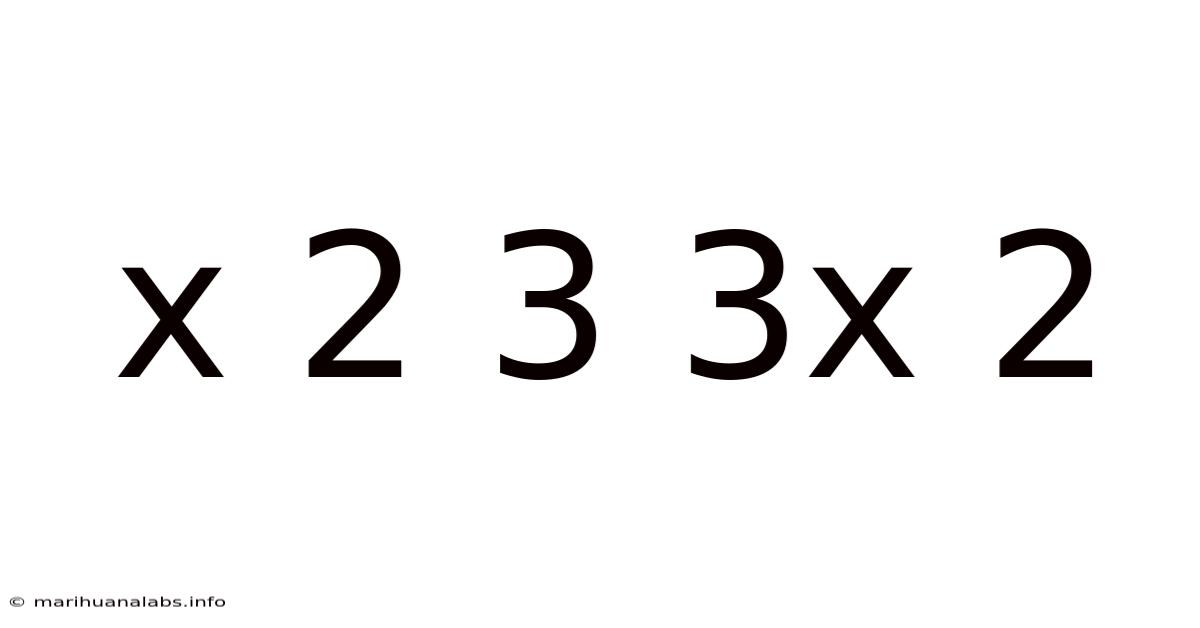
Table of Contents
Deconstructing the Expression: x² + 3x + 3x² + 2
This article delves into the seemingly simple algebraic expression x² + 3x + 3x² + 2, exploring its simplification, applications, and underlying mathematical concepts. We'll cover how to simplify the expression, its graphical representation, and potential real-world applications. This exploration will be accessible to students with a basic understanding of algebra, providing a comprehensive guide to understanding and manipulating this type of expression. We will also address frequently asked questions about simplifying and solving similar expressions.
Understanding the Components
Before we delve into simplifying the expression, let's break down its individual components:
-
x²: This represents x squared, or x multiplied by itself (x * x). It's a quadratic term, meaning it involves a variable raised to the power of 2. The coefficient of this term is implicitly 1.
-
3x: This is a linear term, representing 3 times x. The coefficient is 3.
-
3x²: This is another quadratic term, similar to x², but with a coefficient of 3.
-
2: This is a constant term, a numerical value that doesn't involve the variable x.
Simplifying the Expression
Simplifying this algebraic expression involves combining like terms. Like terms are terms that have the same variable raised to the same power. In this case, we have two quadratic terms (x² and 3x²) and one linear term (3x). The constant term (2) remains separate.
The simplification process is as follows:
-
Identify like terms: We have x² and 3x².
-
Combine like terms: Add the coefficients of the like terms: 1x² + 3x² = 4x².
-
Rewrite the expression: The simplified expression becomes 4x² + 3x + 2.
Therefore, the simplified form of x² + 3x + 3x² + 2 is 4x² + 3x + 2. This is a quadratic expression in its simplest form. It cannot be further simplified without additional information or constraints.
Graphical Representation
The simplified expression, 4x² + 3x + 2, represents a parabola. A parabola is a U-shaped curve that is the graph of a quadratic function. To visualize this, we can plot points on a Cartesian coordinate system. We would choose various values for 'x', substitute them into the equation, and calculate the corresponding 'y' values (where y = 4x² + 3x + 2). These (x, y) pairs would then be plotted, forming the parabola.
The parabola's characteristics, such as its vertex (the lowest or highest point), its axis of symmetry (a vertical line that divides the parabola into two symmetrical halves), and its intercepts (where the parabola crosses the x and y axes), can be determined using techniques from algebra and calculus. For example, the y-intercept (where x = 0) is easily found by substituting x = 0 into the equation, resulting in y = 2. Finding the x-intercepts (where y = 0) is slightly more complex and may involve the quadratic formula or other methods for solving quadratic equations.
The parabola's shape, whether it opens upwards (like a U) or downwards (like an inverted U), is determined by the coefficient of the x² term. Since the coefficient is positive (4), the parabola opens upwards. This means it has a minimum point, which is its vertex.
Applications in Real-World Scenarios
While this may seem like a purely abstract mathematical concept, quadratic expressions like 4x² + 3x + 2 have numerous applications in various fields:
-
Physics: Quadratic equations frequently appear in physics problems involving projectile motion. For example, the height of a projectile launched vertically can be modeled using a quadratic equation where the x variable represents time and the y variable represents height.
-
Engineering: Engineers use quadratic equations to model various aspects of structures and systems, such as the bending of beams or the trajectory of a launched object.
-
Economics: Quadratic functions are employed in economic modeling to represent various relationships between variables, such as cost functions or revenue functions. The vertex of the parabola in a cost function might represent the optimal production level for minimum cost.
-
Computer Graphics: Quadratic curves are extensively used in computer graphics to create smooth, curved lines and shapes.
-
Data Analysis: Quadratic regression, a statistical technique, fits a quadratic equation to a set of data points to model trends and make predictions.
Solving Quadratic Equations
While simplifying the expression is one aspect, it's also important to understand how to solve a quadratic equation, which involves finding the values of x that make the equation equal to zero. Our simplified expression, 4x² + 3x + 2 = 0, is a quadratic equation.
There are several methods for solving quadratic equations:
-
Factoring: This involves expressing the quadratic expression as a product of two linear expressions. However, not all quadratic equations can be factored easily.
-
Quadratic Formula: This is a general formula that can be used to solve any quadratic equation of the form ax² + bx + c = 0:
x = [-b ± √(b² - 4ac)] / 2a
In our case (4x² + 3x + 2 = 0), a = 4, b = 3, and c = 2. Substituting these values into the quadratic formula allows us to find the solutions for x.
-
Completing the Square: This method involves manipulating the quadratic expression to create a perfect square trinomial, making it easier to solve.
Let's apply the quadratic formula to our equation:
x = [-3 ± √(3² - 4 * 4 * 2)] / (2 * 4) x = [-3 ± √(9 - 32)] / 8 x = [-3 ± √(-23)] / 8
Notice that we have a negative number under the square root. This indicates that the solutions for x are complex numbers (involving the imaginary unit i, where i² = -1). This means the parabola does not intersect the x-axis.
Frequently Asked Questions (FAQ)
Q: Can I simplify x² + 3x + 3x² + 2 any further?
A: No, 4x² + 3x + 2 is the simplest form of the expression. You can only combine like terms.
Q: What is the difference between a linear and a quadratic term?
A: A linear term has a variable raised to the power of 1 (e.g., 3x), while a quadratic term has a variable raised to the power of 2 (e.g., 4x²).
Q: How do I find the x-intercepts of the parabola represented by 4x² + 3x + 2?
A: You need to solve the quadratic equation 4x² + 3x + 2 = 0. In this case, the solutions are complex numbers because the discriminant (b² - 4ac) is negative. This means the parabola does not intersect the x-axis.
Q: What if the coefficient of x² was negative?
A: If the coefficient of x² was negative, the parabola would open downwards, meaning it would have a maximum point instead of a minimum point.
Q: Are there other types of polynomial expressions beyond linear and quadratic?
A: Yes, there are cubic (x³), quartic (x⁴), quintic (x⁵), and higher-degree polynomial expressions. The degree of the polynomial is determined by the highest power of the variable.
Conclusion
The seemingly simple expression x² + 3x + 3x² + 2 provides a gateway to understanding fundamental algebraic concepts. Through simplification, we arrive at the quadratic expression 4x² + 3x + 2, which can be graphically represented as a parabola. The exploration of this expression extends beyond simplification to encompass its real-world applications in diverse fields and the methods used to solve the associated quadratic equation. Understanding these concepts provides a solid foundation for further exploration of more complex algebraic and mathematical principles. The ability to simplify, analyze, and solve such expressions is crucial in numerous academic and professional pursuits.
Latest Posts
Latest Posts
-
How Long Is 140 Minutes
Sep 14, 2025
-
Murdock Functions Of The Family
Sep 14, 2025
-
Distinction Between Goods And Services
Sep 14, 2025
-
How Much Is 24 Ounces
Sep 14, 2025
-
Of Mice And Men Setting
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about X 2 3 3x 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.