Whats 60 Percent Of 30
marihuanalabs
Sep 20, 2025 · 5 min read
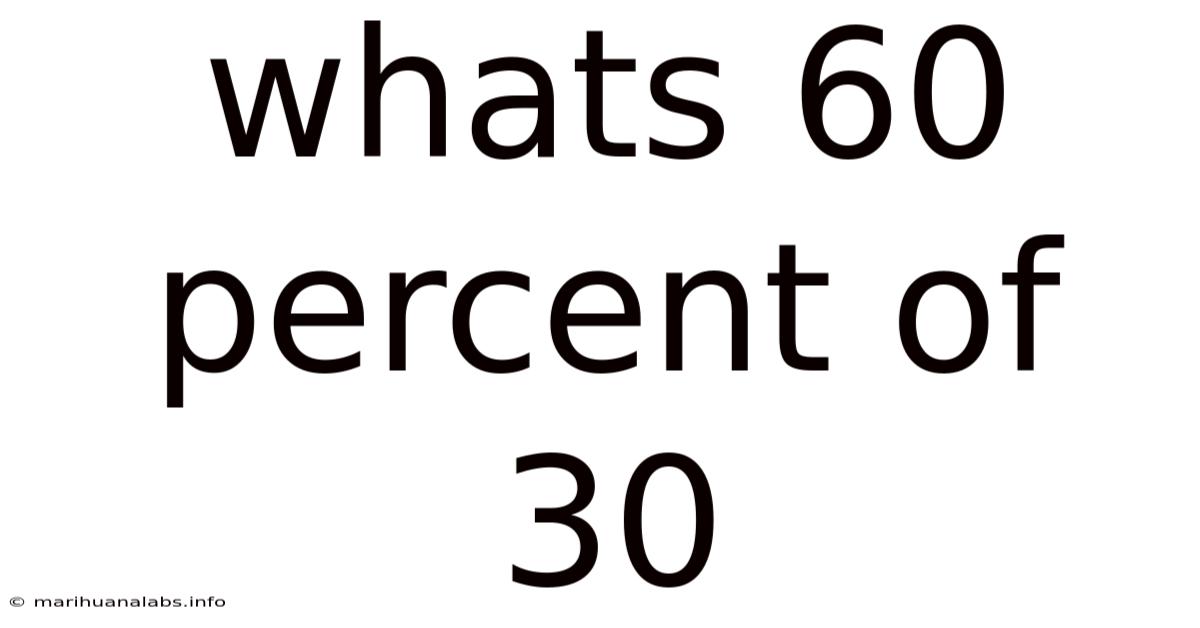
Table of Contents
What's 60 Percent of 30? A Deep Dive into Percentages and Their Applications
Finding 60 percent of 30 might seem like a simple arithmetic problem, easily solvable with a calculator. But this seemingly basic calculation opens the door to a deeper understanding of percentages, their practical applications in various fields, and the underlying mathematical principles. This article will not only provide the answer but will also explore the different methods to solve this problem and delve into the broader context of percentage calculations. We’ll even touch on the history of percentages and their importance in our everyday lives.
Understanding Percentages
A percentage is simply a fraction expressed as a portion of 100. The word "percent" comes from the Latin "per centum," meaning "out of a hundred." Therefore, 60% means 60 out of 100, or 60/100, which simplifies to 3/5. This fundamental understanding forms the basis of all percentage calculations.
Methods to Calculate 60% of 30
There are several ways to calculate 60% of 30. Let's explore the most common approaches:
Method 1: Converting Percentage to Decimal
This is perhaps the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the number.
- Step 1: Convert the percentage to a decimal: 60% is equivalent to 60/100 = 0.60 or 0.6.
- Step 2: Multiply the decimal by the number: 0.6 * 30 = 18
Therefore, 60% of 30 is 18.
Method 2: Using Fractions
This method involves expressing the percentage as a fraction and then multiplying it by the number.
- Step 1: Express the percentage as a fraction: 60% is equivalent to 60/100.
- Step 2: Simplify the fraction: 60/100 simplifies to 3/5.
- Step 3: Multiply the fraction by the number: (3/5) * 30 = 18
Again, we find that 60% of 30 is 18.
Method 3: Proportion Method
This method utilizes the concept of proportions to solve the problem. We set up a proportion where x represents the unknown value (60% of 30).
- Step 1: Set up the proportion: 60/100 = x/30
- Step 2: Cross-multiply: 60 * 30 = 100 * x
- Step 3: Solve for x: 1800 = 100x => x = 1800/100 = 18
This method confirms that 60% of 30 is 18.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in numerous everyday situations and professional fields. Here are a few examples:
- Finance: Calculating interest rates on loans, savings accounts, and investments. Determining discounts on purchases, calculating taxes, and understanding profit margins are all based on percentage calculations. For example, a 10% discount on a $100 item means you save $10.
- Sales and Marketing: Analyzing sales data, tracking conversion rates, and determining the effectiveness of advertising campaigns often involve calculating percentages. A 5% increase in sales compared to the previous year indicates positive growth.
- Science and Research: Presenting experimental data, determining statistical significance, and expressing probabilities frequently utilize percentages. For instance, a 95% confidence interval indicates a high degree of certainty in research findings.
- Education: Grading systems often use percentages to represent student performance. A score of 80% on a test signifies that the student answered 80 out of 100 questions correctly.
- Everyday Life: Calculating tips in restaurants, understanding nutritional information on food labels, and comprehending statistics in news reports all require an understanding of percentages. For example, a 15% tip on a $50 meal is $7.50.
The History of Percentages
The concept of percentages has a rich history. While the use of fractions and ratios dates back to ancient civilizations, the modern concept of percentages emerged in the late Middle Ages. The term "percent" itself came into use in the 15th century, and its usage gradually spread across Europe. The standardized notation using the "%" symbol became common in the 17th century, further solidifying the concept's role in mathematics and commerce. The widespread adoption of decimal notation significantly simplified percentage calculations, contributing to their integration into various aspects of daily life and professional fields.
Beyond the Basics: More Complex Percentage Problems
While finding 60% of 30 is relatively simple, percentage problems can become more complex. Consider these scenarios:
- Finding the original value: If you know that 60% of a number is 18, how do you find the original number? This involves using the formula: Original Number = (Percentage Value / Percentage) * 100. In this case, Original Number = (18 / 60) * 100 = 30.
- Calculating percentage increase or decrease: If a value increases from 30 to 36, what is the percentage increase? This requires calculating the difference (36-30=6), dividing the difference by the original value (6/30=0.2), and multiplying by 100 to get the percentage (0.2*100=20%). Therefore, the percentage increase is 20%.
- Compound percentages: These problems involve applying percentages sequentially. For example, if a price increases by 10% and then decreases by 10%, the final price will not be the same as the original price. This is because the second percentage is applied to the new, increased price.
Frequently Asked Questions (FAQ)
-
Q: What is the easiest way to calculate percentages?
-
A: The easiest method often depends on individual preference and the specific problem. Converting the percentage to a decimal and multiplying is generally a straightforward approach for most calculations.
-
Q: Are there any online tools or calculators for percentage calculations?
-
A: Yes, many online calculators are readily available to assist with percentage calculations. These tools can be especially useful for more complex problems.
-
Q: Why are percentages so important?
-
A: Percentages provide a standardized and easily understandable way to represent proportions and ratios. Their versatility makes them essential tools in various fields, from finance to science and everyday life.
-
Q: How can I improve my understanding of percentages?
-
A: Practice is key! Try working through various percentage problems of increasing difficulty. You can find many practice problems online or in textbooks.
Conclusion
Calculating 60% of 30, while seemingly basic, offers a valuable gateway to understanding the broader concept of percentages and their extensive applications. Mastering percentage calculations equips you with essential skills for various aspects of life, from personal finance to professional endeavors. By understanding the underlying principles and exploring the different calculation methods, you can confidently tackle more complex percentage problems and appreciate their pervasive role in our world. Remember to practice regularly to build your proficiency and confidence in handling percentage calculations. The more you practice, the easier it will become, and you’ll soon find yourself effortlessly navigating the world of percentages.
Latest Posts
Latest Posts
-
Is Ammonia A Weak Base
Sep 20, 2025
-
Crossing Over A Level Biology
Sep 20, 2025
-
Theme For Month Of July
Sep 20, 2025
-
Gb Vs Kb Vs Mb
Sep 20, 2025
-
Blue Flame On Bunsen Burner
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about Whats 60 Percent Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.