Whats 40 Percent Of 60
marihuanalabs
Sep 14, 2025 · 6 min read
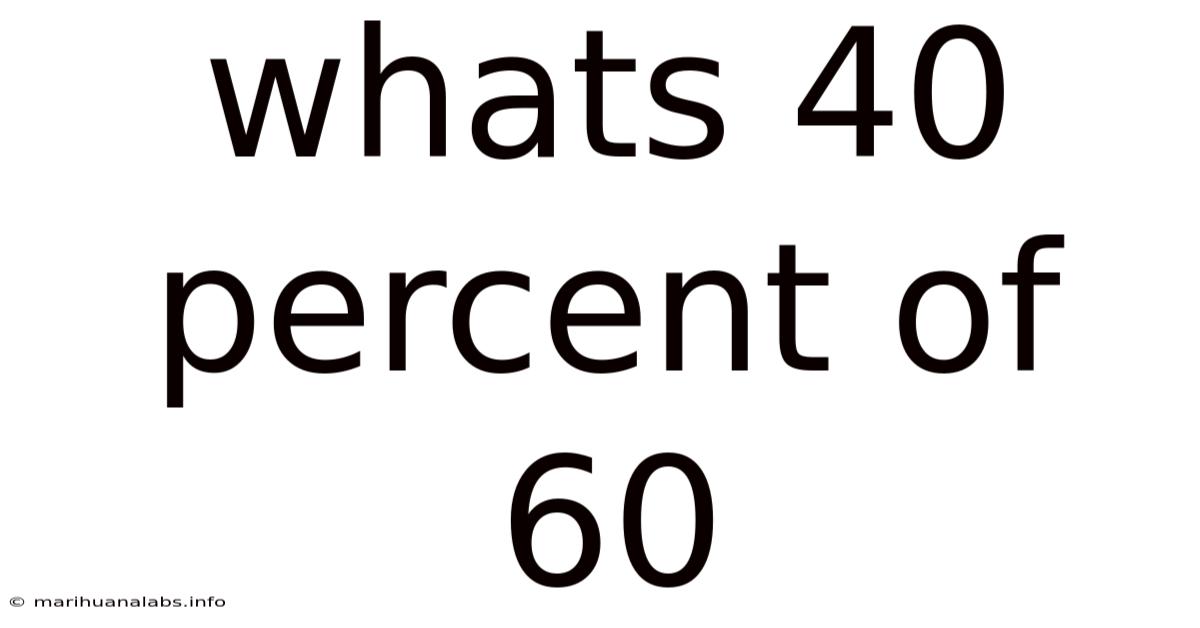
Table of Contents
What's 40 Percent of 60? A Deep Dive into Percentages and Practical Applications
Calculating percentages is a fundamental skill applicable across numerous fields, from everyday budgeting and shopping to complex scientific calculations and financial analysis. Understanding how to determine a percentage of a number is crucial for navigating the numerical world around us. This article will thoroughly explore the question, "What's 40 percent of 60?", providing not only the answer but also a comprehensive understanding of the underlying principles and various methods for solving percentage problems. We will delve into the mathematical concepts, explore different calculation approaches, and discuss real-world applications to solidify your understanding.
Understanding Percentages: The Basics
A percentage is a fraction expressed as a number out of 100. The symbol "%" represents "percent," meaning "per hundred." Therefore, 40% means 40 out of 100, or 40/100, which simplifies to 2/5. This fraction represents a portion or ratio of a whole. To calculate a percentage of a number, we essentially find that specific fraction of the number.
Method 1: Using the Decimal Equivalent
The most straightforward method to find 40% of 60 is to convert the percentage to its decimal equivalent and then multiply.
-
Step 1: Convert the percentage to a decimal: To convert a percentage to a decimal, divide the percentage by 100. In this case, 40% becomes 40 ÷ 100 = 0.40 or simply 0.4.
-
Step 2: Multiply the decimal by the number: Now, multiply the decimal equivalent (0.4) by the number you want to find the percentage of (60). This gives us 0.4 * 60 = 24.
Therefore, 40% of 60 is $\boxed{24}$.
Method 2: Using Fractions
As mentioned earlier, 40% can be expressed as the fraction 40/100. We can use this fraction to calculate 40% of 60.
-
Step 1: Express the percentage as a fraction: 40% = 40/100
-
Step 2: Simplify the fraction (if possible): The fraction 40/100 can be simplified by dividing both the numerator and denominator by their greatest common divisor, which is 20. This simplifies to 2/5.
-
Step 3: Multiply the fraction by the number: Now, multiply the simplified fraction (2/5) by 60: (2/5) * 60 = (2 * 60) / 5 = 120 / 5 = 24.
Again, we find that 40% of 60 is $\boxed{24}$.
Method 3: Using Proportions
A proportion is a statement that two ratios are equal. We can set up a proportion to solve for 40% of 60.
-
Step 1: Set up the proportion: We can express the problem as a proportion: x/60 = 40/100, where 'x' represents the unknown value (40% of 60).
-
Step 2: Cross-multiply: Cross-multiply the terms in the proportion: 100x = 40 * 60
-
Step 3: Solve for x: 100x = 2400. Divide both sides by 100 to isolate x: x = 2400 / 100 = 24.
This method confirms that 40% of 60 is $\boxed{24}$.
Beyond the Basics: Understanding the Application
The calculation "40% of 60" might seem simple in isolation, but its application spans a wide range of real-world scenarios. Let's explore some examples:
-
Discounts: Imagine a store offering a 40% discount on an item priced at $60. The discount amount would be 40% of $60, which is $24. The final price after the discount would be $60 - $24 = $36.
-
Tax Calculations: If a sales tax is 40% and the pre-tax price of an item is $60, the tax amount would be $24. The total price including tax would be $60 + $24 = $84.
-
Grade Calculations: Suppose a student scored 40 out of 60 on a test. To determine the percentage score, we'd calculate (40/60) * 100% = 66.67%.
-
Financial Analysis: In finance, percentages are used extensively. For instance, calculating profit margins, investment returns, or interest rates often involves percentage calculations. Understanding 40% of 60 could help in scenarios involving calculating a 40% return on a $60 investment.
-
Survey Results: In data analysis, interpreting survey results often involves calculating percentages. If 40 out of 60 respondents answered "yes" to a question, the percentage of "yes" responses would be 66.67%.
These are just a few examples; percentage calculations are essential in various contexts, making it a crucial skill to master.
Advanced Concepts and Related Calculations
While we've focused on finding 40% of 60, let's explore some related concepts and calculations that build upon this foundation:
-
Finding the Percentage One Number Represents of Another: If you know that 24 is a portion of 60, you can calculate the percentage it represents using the formula: (Part/Whole) * 100%. In this case, (24/60) * 100% = 40%.
-
Finding the Original Number Given a Percentage: If you know that 24 represents 40% of a number, you can solve for the original number by setting up a proportion: 24/x = 40/100. Solving for x gives us x = 60.
-
Calculating Percentage Increase or Decrease: Percentage changes are frequently encountered. If a value increases from 60 to 84, the percentage increase is calculated as: [(New Value - Original Value) / Original Value] * 100% = [(84 - 60) / 60] * 100% = 40%. Similarly, a decrease can be calculated using the same formula.
Frequently Asked Questions (FAQ)
-
Q: What are some common mistakes when calculating percentages?
- A: A common mistake is incorrectly converting percentages to decimals. Remember to divide by 100. Another frequent error is using the wrong order of operations when calculating more complex percentage problems involving addition or subtraction.
-
Q: Are there online calculators for percentage calculations?
- A: Yes, many online calculators are readily available to perform percentage calculations. However, understanding the underlying principles is crucial for solving diverse problems.
-
Q: How can I improve my skills in calculating percentages?
- A: Practice regularly with various problems. Start with simple calculations and gradually move to more complex ones. Understanding different methods, like using decimals, fractions, and proportions, allows you to approach problems from different angles.
-
Q: Why is understanding percentages important?
- A: Percentages are ubiquitous in daily life, from understanding discounts and taxes to interpreting data and making financial decisions. Mastering percentage calculations empowers you to analyze information critically and make informed choices.
Conclusion
This comprehensive guide has explored the seemingly simple question, "What's 40 percent of 60?", but in doing so, it has illuminated the broader world of percentage calculations. We've demonstrated multiple methods for arriving at the answer (24) and explored the various real-world applications of this fundamental mathematical concept. By understanding these principles and practicing regularly, you can confidently tackle percentage problems in any context, enhancing your numeracy skills and empowering you to make informed decisions in your personal and professional life. Remember, mastering percentages is not just about memorizing formulas; it's about understanding the underlying concepts and their practical implications. This understanding will serve you well in various aspects of your life.
Latest Posts
Latest Posts
-
Book The Emperors New Clothes
Sep 14, 2025
-
Four Types Of Food Contamination
Sep 14, 2025
-
Prisoner Number In Les Miserables
Sep 14, 2025
-
Group Of Cattle Is Called
Sep 14, 2025
-
Sulfate Ion Lewis Dot Structure
Sep 14, 2025
Related Post
Thank you for visiting our website which covers about Whats 40 Percent Of 60 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.