Whats 3 4 Of 16
marihuanalabs
Sep 08, 2025 · 5 min read
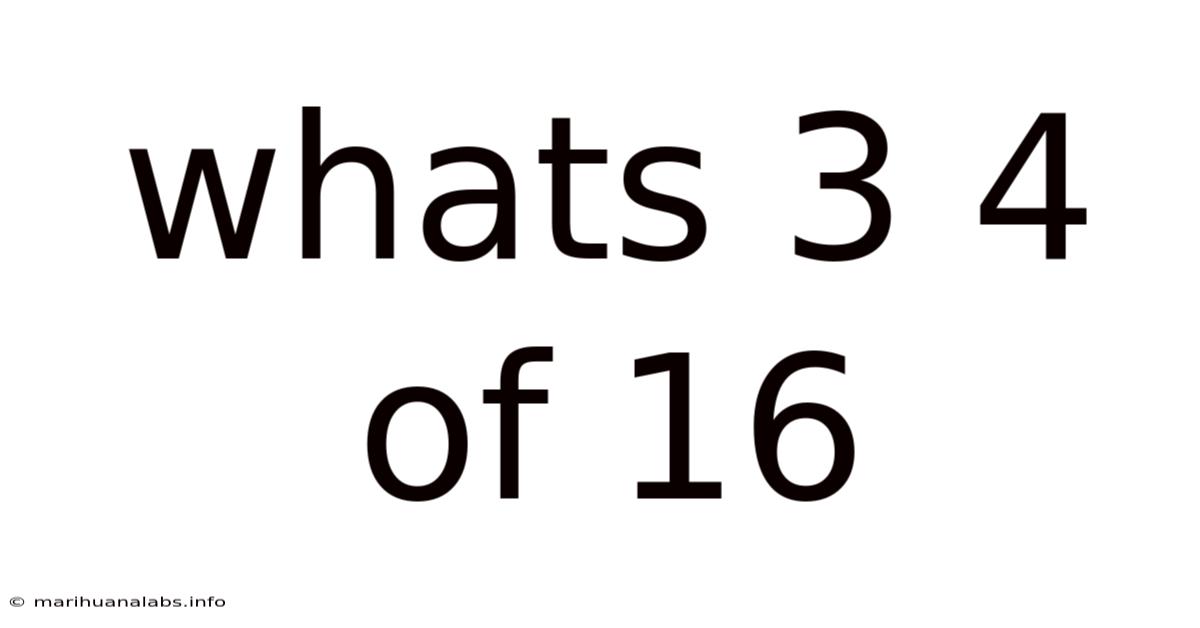
Table of Contents
What's ¾ of 16? A Deep Dive into Fractions and Their Applications
Finding ¾ of 16 might seem like a simple arithmetic problem, but it opens the door to a deeper understanding of fractions, their manipulation, and their widespread applications in various fields. This article will not only answer the question directly but also explore the underlying concepts, different methods of solving the problem, and real-world examples where this type of calculation is crucial.
Understanding Fractions: A Quick Refresher
A fraction represents a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates how many parts you have, and the denominator indicates how many equal parts the whole is divided into. For example, in the fraction ¾, 3 is the numerator and 4 is the denominator. This means we have 3 out of 4 equal parts of a whole.
Method 1: Direct Multiplication
The most straightforward way to calculate ¾ of 16 is through direct multiplication. We can express "of" as multiplication. Therefore, ¾ of 16 can be written as:
(¾) * 16
To perform this multiplication, we multiply the numerator (3) by 16 and then divide the result by the denominator (4):
(3 * 16) / 4 = 48 / 4 = 12
Therefore, ¾ of 16 is 12.
Method 2: Finding a Unit Fraction
Another approach involves finding the value of one-fourth (¼) of 16 first, and then multiplying the result by 3.
- Find ¼ of 16: Divide 16 by 4: 16 / 4 = 4
- Multiply by 3: Since we need ¾, multiply the result from step 1 by 3: 4 * 3 = 12
This method reinforces the understanding of fractions as parts of a whole. It shows that we can break down the problem into smaller, more manageable steps.
Method 3: Visual Representation
Visualizing the problem can be helpful, especially for beginners. Imagine a rectangle divided into four equal parts. Each part represents ¼ of the whole. If the whole rectangle represents 16, then each part represents 4 (16 / 4 = 4). To find ¾, we simply shade three of these four parts. The shaded area represents 3 * 4 = 12. This visual method aids in grasping the concept of fractions and their relationship to the whole.
Real-World Applications: Where Fractions Matter
Understanding how to calculate fractions like ¾ of 16 isn't just an academic exercise. It's a fundamental skill applicable in numerous real-world scenarios:
- Cooking and Baking: Recipes often require fractional amounts of ingredients. For example, a recipe might call for ¾ cup of flour. Knowing how to calculate this accurately is essential for successful baking.
- Construction and Engineering: Precise measurements are crucial in construction and engineering projects. Calculations involving fractions are frequently used to determine accurate dimensions and material quantities.
- Finance and Budgeting: Understanding fractions is vital for managing finances and budgeting effectively. Calculating percentages (which are essentially fractions expressed as a part of 100) is fundamental to understanding interest rates, discounts, and taxes.
- Data Analysis and Statistics: Fractions and proportions are extensively used in data analysis and statistics. They help in expressing relationships between different data points and drawing meaningful conclusions.
- Sales and Discounts: Calculating discounts often involves working with fractions. For instance, a "25% off" sale is equivalent to finding ¾ of the original price.
- Geometry and Measurement: Many geometric calculations involve fractions, especially when dealing with areas and volumes of shapes.
- Everyday Life: From sharing food equally among friends to understanding sales promotions, fractions are part of our daily lives.
Expanding the Concept: Working with More Complex Fractions
The principles discussed above can be applied to more complex fraction problems. Let's consider a slightly more challenging example: What is 5/8 of 24?
-
Direct Multiplication: (5/8) * 24 = (5 * 24) / 8 = 120 / 8 = 15
-
Finding a Unit Fraction: First, find 1/8 of 24: 24 / 8 = 3. Then, multiply by 5: 3 * 5 = 15
The solution remains the same regardless of the method used. This consistency reinforces the fundamental principles of fraction calculation.
Dealing with Improper Fractions
An improper fraction is one where the numerator is larger than the denominator (e.g., 7/4). When calculating with improper fractions, the same principles apply, but the result might be a whole number or a mixed number (a whole number and a fraction).
For example, let's calculate 7/4 of 8:
(7/4) * 8 = (7 * 8) / 4 = 56 / 4 = 14
In this case, the result is a whole number.
Converting Between Fractions, Decimals, and Percentages
Fractions, decimals, and percentages are all different ways of expressing the same value. Understanding how to convert between these forms is crucial for practical applications.
- Fraction to Decimal: Divide the numerator by the denominator. For example, ¾ = 3 ÷ 4 = 0.75
- Decimal to Fraction: Express the decimal as a fraction with a denominator of a power of 10 (e.g., 0.75 = 75/100). Then simplify the fraction if possible (75/100 simplifies to ¾).
- Fraction to Percentage: Convert the fraction to a decimal, then multiply by 100 and add a percent sign. For example, ¾ = 0.75 * 100% = 75%
- Percentage to Fraction: Divide the percentage by 100 and simplify the resulting fraction. For example, 75% = 75/100 = ¾
Frequently Asked Questions (FAQ)
-
Q: What if I need to find a fraction of a fraction?
- A: This involves multiplying the fractions. For example, to find ½ of ¾, you would multiply (½) * (¾) = (13)/(24) = 3/8.
-
Q: How do I simplify fractions?
- A: Find the greatest common divisor (GCD) of the numerator and denominator, and divide both by the GCD. For example, to simplify 12/16, the GCD is 4. Dividing both numerator and denominator by 4 gives 3/4.
-
Q: What if I have a mixed number (a whole number and a fraction)?
- A: Convert the mixed number to an improper fraction before performing calculations. For example, 1 ½ = (1 * 2 + 1) / 2 = 3/2.
Conclusion
Finding ¾ of 16, while seemingly simple, unveils a broader understanding of fractions, their manipulation, and their significance in diverse fields. Mastering fraction calculations is a fundamental skill that transcends academic boundaries, empowering individuals to confidently navigate numerous real-world situations, from everyday tasks to complex professional endeavors. By understanding the various methods and their applications, we can appreciate the power and versatility of fractions in our daily lives. The ability to solve problems like this is not merely about finding the answer (which is 12), but about developing a deeper mathematical intuition and problem-solving skillset that will serve you well in countless future endeavors.
Latest Posts
Latest Posts
-
D Major Scale In Piano
Sep 09, 2025
-
What Is 18km In Miles
Sep 09, 2025
-
Chords In D Major Scale
Sep 09, 2025
-
Quotes About Snowball Animal Farm
Sep 09, 2025
-
Duchess Of Malfi Plot Summary
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about Whats 3 4 Of 16 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.