Whats 25 Percent Of 50
marihuanalabs
Sep 17, 2025 · 5 min read
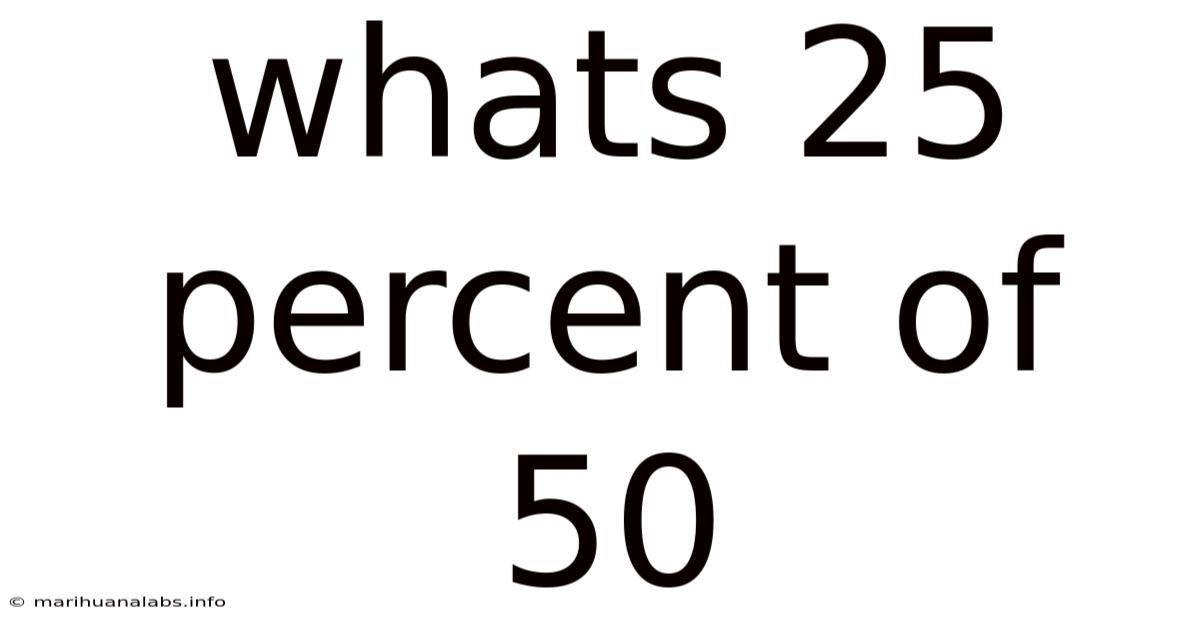
Table of Contents
What's 25 Percent of 50? A Deep Dive into Percentages and Their Applications
Finding 25 percent of 50 might seem like a simple calculation, but it opens the door to understanding a fundamental concept in mathematics and its widespread applications in everyday life. This article will not only answer the question directly but will also delve into the underlying principles of percentages, explore different methods for calculating them, and showcase their relevance in various fields. We'll even tackle some common percentage-related problems and frequently asked questions. By the end, you'll not only know that 25% of 50 is 12.5, but you'll also possess a robust understanding of how to tackle percentage problems confidently.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The word "percent" itself comes from the Latin "per centum," meaning "out of a hundred." Therefore, 25% literally means 25 out of 100, or 25/100, which simplifies to 1/4. This fundamental understanding is crucial for tackling any percentage problem.
Understanding percentages is essential for numerous real-world applications, from calculating discounts and sales tax to understanding financial reports, interpreting statistical data, and even cooking! Mastering this concept empowers you to make informed decisions in various aspects of your life.
Calculating 25% of 50: Three Methods
There are several ways to calculate 25% of 50. Let's explore three common methods:
Method 1: Using the Fraction Equivalent
As we established, 25% is equivalent to the fraction 1/4. Therefore, to find 25% of 50, we can simply multiply 50 by 1/4:
50 * (1/4) = 50/4 = 12.5
This method is straightforward and particularly useful when dealing with simple percentages like 25%, 50%, and 75%, which have easy-to-remember fraction equivalents.
Method 2: Converting Percentage to Decimal
Another common method involves converting the percentage to its decimal equivalent. To do this, we divide the percentage by 100. For 25%, this is:
25% / 100 = 0.25
Now, we multiply this decimal by the number we want to find the percentage of:
0.25 * 50 = 12.5
This method is versatile and works well for any percentage, making it a widely applicable approach.
Method 3: Using Proportion
This method involves setting up a proportion. We know that 25% is to 100% as 'x' (the unknown value) is to 50. We can express this as:
25/100 = x/50
To solve for 'x', we cross-multiply:
25 * 50 = 100 * x
1250 = 100x
x = 1250/100 = 12.5
This method might seem more complex at first, but it's particularly useful for solving more challenging percentage problems where other methods might be less intuitive.
Real-World Applications of Percentages
Percentages are ubiquitous in our daily lives, appearing in a vast array of contexts. Here are a few examples:
-
Sales and Discounts: Stores frequently advertise discounts as percentages, such as "25% off" or "50% off." Understanding percentages allows you to quickly calculate the final price of an item after a discount.
-
Taxes: Sales tax, income tax, and other taxes are often expressed as percentages. Knowing how to calculate percentages helps you determine the total cost of a purchase including tax, or to understand the amount of tax you'll owe.
-
Finance: Interest rates on loans and savings accounts are usually expressed as percentages. Understanding percentages helps you compare different financial products and make informed financial decisions.
-
Statistics and Data Analysis: Percentages are fundamental to interpreting statistical data. They allow us to express proportions and trends in a clear and concise manner. For example, understanding the percentage of people who support a particular candidate in an election provides valuable insight.
-
Science and Engineering: Percentages are utilized in various scientific and engineering calculations, including determining concentrations, efficiencies, and error margins.
-
Cooking and Baking: Recipes often include ingredients listed as percentages of the total weight or volume. This allows for accurate scaling of recipes up or down.
Beyond the Basics: Tackling More Complex Percentage Problems
While finding 25% of 50 is a simple calculation, many real-world percentage problems are more complex. Let's look at some examples:
Example 1: Finding the Original Price After a Discount
A shirt is on sale for $30 after a 20% discount. What was the original price?
Let 'x' represent the original price. The discount is 20% of x, or 0.2x. The sale price is the original price minus the discount:
x - 0.2x = 30
0.8x = 30
x = 30 / 0.8 = $37.50
Therefore, the original price was $37.50.
Example 2: Calculating Percentage Increase or Decrease
A stock price increased from $50 to $60. What is the percentage increase?
The increase is $60 - $50 = $10. To find the percentage increase, we divide the increase by the original price and multiply by 100:
(10 / 50) * 100 = 20%
The stock price increased by 20%.
Frequently Asked Questions (FAQ)
Q: What if I need to calculate a percentage that doesn't have a simple fraction equivalent?
A: The decimal method is the most versatile for any percentage. Simply divide the percentage by 100 and multiply by the number.
Q: How do I calculate the percentage of a percentage?
A: Convert both percentages to decimals and then multiply them. For example, to find 10% of 25%, you would calculate 0.10 * 0.25 = 0.025, or 2.5%.
Q: Are there any online calculators or tools that can help?
A: Yes, many online calculators are available that can assist with percentage calculations. However, understanding the underlying principles remains crucial for problem-solving.
Q: What are some common mistakes to avoid when working with percentages?
A: Common mistakes include misinterpreting the base value, incorrectly converting percentages to decimals, and failing to consider the context of the problem. Always double-check your work and ensure you understand what the question is asking.
Conclusion: Mastering Percentages for a Brighter Future
Understanding percentages is not just about solving simple arithmetic problems; it's a foundational skill with far-reaching implications across various aspects of life. Whether you're shopping for a discounted item, analyzing financial statements, or interpreting scientific data, the ability to confidently calculate and interpret percentages will empower you to make informed decisions and navigate the complexities of the modern world. Remember the three methods outlined – using fraction equivalents, converting to decimals, and setting up proportions – and practice regularly to solidify your understanding. You’ve already successfully calculated that 25% of 50 is 12.5 – now, go forth and conquer the world of percentages!
Latest Posts
Latest Posts
-
Recently Crossword Clue 2 4
Sep 17, 2025
-
What Is 1 Of 500
Sep 17, 2025
-
Lake Of Isle Of Innisfree
Sep 17, 2025
-
91 Degrees F To C
Sep 17, 2025
-
How Long Is 0 5 Meters
Sep 17, 2025
Related Post
Thank you for visiting our website which covers about Whats 25 Percent Of 50 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.