What Is X 3 3
marihuanalabs
Sep 15, 2025 · 6 min read
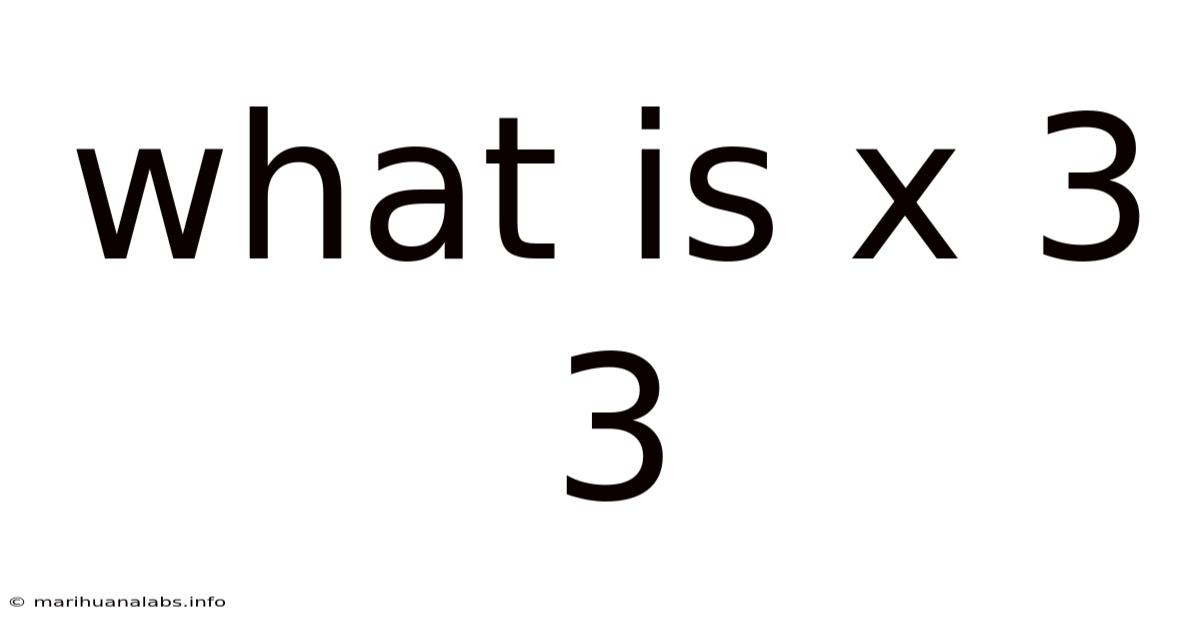
Table of Contents
Decoding "x³³": Exploring the Mathematical Concept of Exponentiation and Beyond
The expression "x³³" might seem intimidating at first glance, but understanding its meaning unlocks a fascinating world within mathematics. This article delves into the core concept of exponentiation, explaining what "x³³" represents, how it's calculated, and its broader implications within various mathematical fields. We'll explore its applications, potential complexities, and even touch upon related concepts to provide a comprehensive understanding. By the end, you’ll not only understand what x³³ means but also gain a stronger foundation in exponential mathematics.
Understanding Exponentiation: The Fundamentals
At its heart, "x³³" is an example of exponentiation, a mathematical operation that involves raising a base (in this case, 'x') to a certain power (in this case, '33'). This power, also known as the exponent or index, indicates how many times the base is multiplied by itself. Let's break it down:
-
Base (x): This is the number that is being multiplied repeatedly. It can be any real number, a complex number, or even a variable.
-
Exponent (33): This number indicates the number of times the base is multiplied by itself. In our example, 'x' is multiplied by itself 32 times.
Therefore, x³³ = x * x * x * x * ... * x (33 times)
A simpler example would be 2³. This means 2 * 2 * 2 = 8. The exponent tells us how many times the base is used as a factor in the multiplication.
Calculating x³³: Methods and Considerations
Calculating x³³ directly by repeated multiplication is impractical for most values of x, especially when dealing with larger exponents. Fortunately, mathematics provides more efficient methods:
-
Iterative Multiplication: While inefficient for large exponents like 33, this involves repeatedly multiplying x by itself. This is conceptually straightforward but becomes cumbersome very quickly.
-
Logarithms and Exponentials: For larger exponents, logarithms and exponentials are indispensable tools. Logarithms allow us to transform exponential expressions into simpler forms that are easier to manipulate. For example, if we want to solve for x in an equation like x³³ = y, we could use logarithms to find x.
-
Calculators and Software: Modern calculators and mathematical software packages are designed to handle large exponents efficiently and accurately. These tools utilize optimized algorithms to compute x³³ with speed and precision.
-
Computational Considerations: It's important to note that the accuracy of the calculation depends on the precision of the system used. Floating-point arithmetic in computers can introduce small rounding errors, especially with very large numbers or exponents.
Extending the Concept: Beyond Whole Number Exponents
The concept of exponentiation extends beyond whole numbers. We can also work with:
-
Zero Exponent (x⁰): Any non-zero number raised to the power of zero is equal to 1 (x⁰ = 1, where x ≠ 0). This is a fundamental rule in exponentiation.
-
Negative Exponents (x⁻ⁿ): A negative exponent indicates the reciprocal of the base raised to the positive exponent. For example, x⁻³ = 1/x³.
-
Fractional Exponents (x^(m/n)): A fractional exponent signifies the nth root of the base raised to the mth power. For example, x^(2/3) is the cube root of x²
Applications of Exponentiation: Real-World Examples
Exponentiation plays a crucial role in many areas of mathematics and science:
-
Compound Interest: The growth of money invested with compound interest is modeled using exponential functions. The formula A = P(1 + r/n)^(nt) exemplifies this, where A is the future value, P is the principal amount, r is the annual interest rate, n is the number of times interest is compounded yearly, and t is the number of years.
-
Exponential Growth and Decay: Many natural phenomena, such as population growth, radioactive decay, and the spread of diseases, are described using exponential functions. These models accurately predict changes over time based on exponential growth or decay rates.
-
Physics and Engineering: Exponentiation appears extensively in physics and engineering, particularly in areas like mechanics, electromagnetism, and quantum mechanics. Exponential functions describe phenomena such as the decay of radioactive substances or the behavior of oscillating systems.
-
Computer Science: Exponential functions are fundamental in analyzing the efficiency of algorithms. The time complexity of certain algorithms is described using exponential notation, helping programmers understand how the runtime scales with the input size.
Complex Numbers and Exponentiation
Exponentiation can be extended to complex numbers. A complex number has a real and an imaginary part (a + bi, where 'a' and 'b' are real numbers and 'i' is the imaginary unit, √-1). Raising a complex number to a power involves utilizing Euler's formula, which connects exponential functions with trigonometric functions:
e^(ix) = cos(x) + i sin(x)
This formula allows for the calculation of complex exponentials, which have significant applications in various fields such as signal processing and electrical engineering.
Further Exploration: Related Concepts
To fully grasp the concept of x³³, it’s helpful to explore related mathematical ideas:
-
Polynomial Functions: Polynomials involve terms with variables raised to various powers (including exponents). Understanding polynomials builds upon the foundations laid by exponentiation.
-
Power Series: Power series are infinite sums of terms with increasing exponents. They provide a powerful tool for approximating functions and solving differential equations.
-
Taylor and Maclaurin Series: These specific types of power series offer representations of functions as infinite sums of terms involving their derivatives. They are vital in calculus and its applications.
-
Differential Equations: Many differential equations involve exponential functions as solutions, showcasing the fundamental role of exponentiation in modeling dynamic systems.
Frequently Asked Questions (FAQ)
Q: What if x is negative in x³³?
A: If x is negative, the result will depend on whether the exponent (33) is even or odd. If the exponent is odd (like 33), the result will be negative. If the exponent is even, the result will be positive.
Q: How do I calculate x³³ without a calculator for a large value of x?
A: For large values of x, manual calculation is impractical. Utilizing logarithms and exponentials, or using software/calculators, are necessary for accurate and efficient computation.
Q: What are some common mistakes when working with exponents?
A: Common mistakes include incorrect application of exponent rules (like adding exponents when multiplying bases), confusion with negative or fractional exponents, and overlooking the order of operations (PEMDAS/BODMAS).
Q: Is there a limit to how large an exponent can be?
A: Theoretically, there’s no limit to the size of an exponent. However, practical limitations arise due to computational constraints and potential for rounding errors with extremely large numbers.
Q: How does x³³ relate to other mathematical concepts?
A: x³³ is fundamentally tied to concepts like logarithms, polynomial functions, power series, and differential equations, highlighting its importance within a larger mathematical framework.
Conclusion: Mastering the Power of Exponentiation
Understanding "x³³" requires a firm grasp of exponentiation's fundamental principles and its broader implications. While direct calculation for large exponents might be challenging, the use of logarithms, calculators, or software makes this feasible. The applications of exponentiation extend far beyond simple calculations, playing a crucial role in diverse fields from finance to physics. This comprehensive exploration should not only clarify the meaning of x³³ but also equip you with a deeper understanding of the power and versatility of exponential mathematics. Further exploration into related concepts will undoubtedly deepen your appreciation of its fundamental role within the mathematical landscape.
Latest Posts
Latest Posts
-
The Thorn Birds Missing Years
Sep 15, 2025
-
72 5kg In Stone And Pounds
Sep 15, 2025
-
Sample Setting Of A Story
Sep 15, 2025
-
Ugly Duckling Song With Lyrics
Sep 15, 2025
-
Theme Of Ambition In Macbeth
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is X 3 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.