What Is Half Of 36
marihuanalabs
Sep 07, 2025 · 6 min read
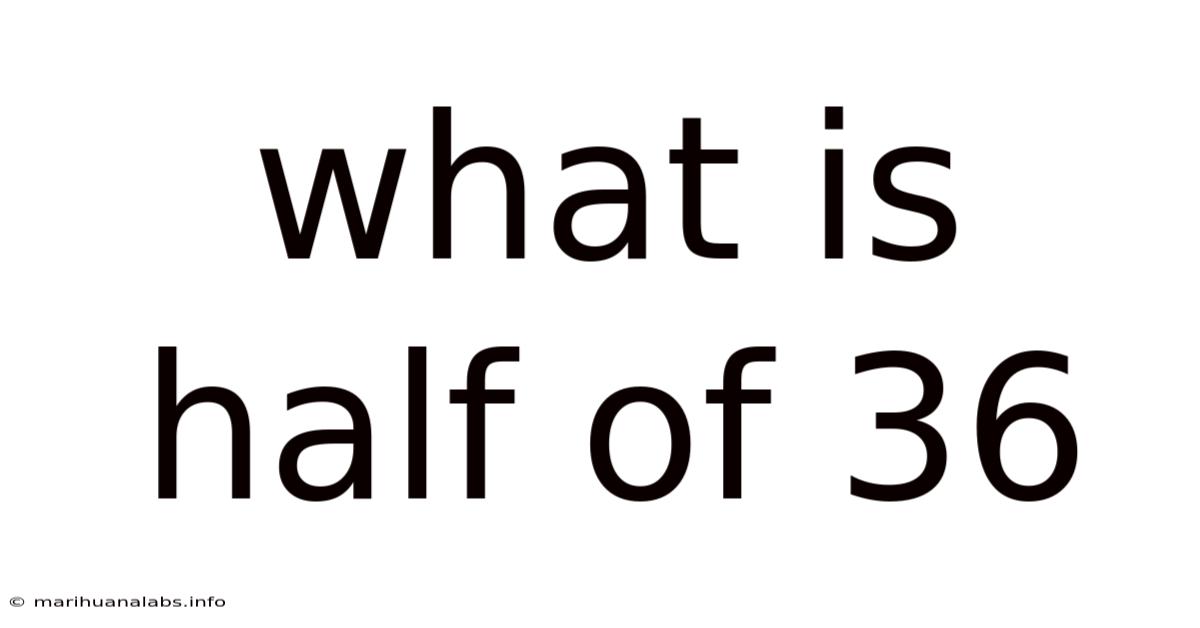
Table of Contents
What is Half of 36? A Deep Dive into Division and its Applications
What is half of 36? The answer, of course, is 18. But this seemingly simple question opens the door to a fascinating exploration of fundamental mathematical concepts, their practical applications, and the underlying logic that governs them. This article will delve into the meaning of "half," the process of division, and how understanding this basic arithmetic operation can unlock a deeper appreciation for mathematics and its role in our daily lives. We'll move beyond the simple answer and explore the various ways this concept manifests itself in different fields and contexts.
Understanding Division: The Foundation of Finding Half
Before we dissect the problem of finding half of 36, let's establish a solid understanding of division. Division is one of the four basic arithmetic operations, alongside addition, subtraction, and multiplication. It represents the process of splitting a quantity into equal parts. In essence, division answers the question: "How many times does one number fit into another?"
When we say "half of 36," we're essentially asking: "What number, when multiplied by 2, equals 36?" This phrasing highlights the inverse relationship between multiplication and division. They are opposite operations that undo each other. If you multiply a number by 2 and then divide the result by 2, you get back to the original number.
The mathematical representation of "half of 36" is written as: 36 ÷ 2 or 36/2. Both notations represent the same operation: dividing 36 into two equal parts. The answer, as we know, is 18. Each part is 18.
Methods for Finding Half: Different Approaches to the Same Solution
There are several ways to calculate half of 36, catering to different levels of mathematical understanding and preferred methods.
-
Direct Division: The most straightforward approach is simply dividing 36 by 2 using long division, short division, or even a calculator. This directly applies the definition of division to find the answer.
-
Repeated Subtraction: We can also find half of 36 by repeatedly subtracting 2 from 36 until we reach 0. The number of times we subtract 2 represents half of 36. This method is more intuitive for younger learners, illustrating the concept of splitting into equal parts through repeated removal.
-
Halving Technique: For numbers that are easily divisible by 2, we can use a mental math technique. We know that half of 30 is 15, and half of 6 is 3. Adding these two halves (15 + 3) gives us the answer, 18. This method highlights the distributive property of division.
-
Fractional Representation: "Half" can be expressed as the fraction 1/2. Therefore, finding half of 36 is the same as calculating (1/2) * 36. This approach introduces the concept of fractions and their role in representing parts of a whole. Multiplying 36 by the numerator (1) and dividing by the denominator (2) yields the same result: 18.
Beyond the Basics: Applications of Finding Half
The seemingly simple task of finding half of 36 has far-reaching applications across various fields:
-
Everyday Life: Dividing quantities in half is a common occurrence in daily life. Sharing snacks equally between two people, splitting a bill, or calculating half a recipe are all examples where this basic mathematical skill is essential.
-
Geometry and Measurement: Calculating the midpoint of a line segment, finding the radius of a circle given its diameter, or determining half the area of a shape all involve dividing a quantity by 2. These applications are fundamental to geometry and spatial reasoning.
-
Data Analysis and Statistics: In statistics, finding the median of a data set often involves dividing the data into two halves. The median represents the middle value, providing a measure of central tendency.
-
Finance and Budgeting: Calculating half of a budget, splitting investment returns, or determining half the interest rate are all instances where dividing by 2 is crucial for financial calculations.
-
Computer Science: In programming, the concept of "half" is often used in algorithms for searching, sorting, and dividing tasks between multiple processors. Binary search, a highly efficient algorithm, repeatedly divides the search space in half.
-
Physics and Engineering: Many physical phenomena and engineering designs involve halving quantities. For example, reducing the mass of an object by half can significantly affect its acceleration. Similarly, halving the resistance in an electrical circuit affects the current flow.
Mathematical Extensions and Deeper Concepts
The simple problem of finding half of 36 provides a springboard for exploring more advanced mathematical concepts:
-
Proportions and Ratios: Finding half is a specific case of a broader concept: proportions. A ratio of 1:2 signifies one part to two parts, which is equivalent to half. Understanding proportions is essential for scaling, comparing quantities, and solving various mathematical problems.
-
Percentage Calculations: Half is equivalent to 50%. Understanding the relationship between fractions, decimals, and percentages is crucial for calculating discounts, taxes, and many other real-world applications.
-
Decimal Representation: Half can also be represented as the decimal 0.5. Working with decimals allows for greater precision and flexibility in calculations, especially when dealing with quantities that are not easily divisible by 2.
Frequently Asked Questions (FAQ)
-
What if I need to find a third of 36 instead of half? To find a third of 36, you would divide 36 by 3, resulting in 12. This illustrates how the concept extends beyond halves to other fractions.
-
How can I find half of an odd number? Finding half of an odd number results in a decimal or fraction. For instance, half of 35 is 17.5 or 17 1/2. This highlights the fact that division doesn't always result in a whole number.
-
Are there other ways to represent "half"? Yes, "half" can be represented as 1/2, 0.5, 50%, and even as a ratio of 1:1. These different representations underscore the versatility and interconnectedness of mathematical concepts.
Conclusion: The Power of Simple Arithmetic
Finding half of 36, while seemingly trivial, reveals a wealth of mathematical concepts and their practical applications. From the fundamentals of division and its inverse relationship with multiplication to the broader context of proportions, percentages, and various real-world applications, this simple problem serves as a microcosm of the power and relevance of mathematics in our daily lives. Understanding these basic operations isn't just about memorizing formulas; it's about developing a deeper understanding of how numbers interact, how quantities can be manipulated, and how this knowledge can be applied to solve real-world problems. The next time you face a similar problem, remember the underlying principles and the vast potential of seemingly simple mathematical concepts. The answer might be simple, but the journey to understanding it can be profound.
Latest Posts
Latest Posts
-
Difference Between Greed And Gluttony
Sep 08, 2025
-
Name Of Group Of Horses
Sep 08, 2025
-
Its A Far Better Thing
Sep 08, 2025
-
Jack And The Beanstalk Book
Sep 08, 2025
-
The Pixies Que Sera Sera
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 36 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.