What Is Half Of 28
marihuanalabs
Sep 08, 2025 · 5 min read
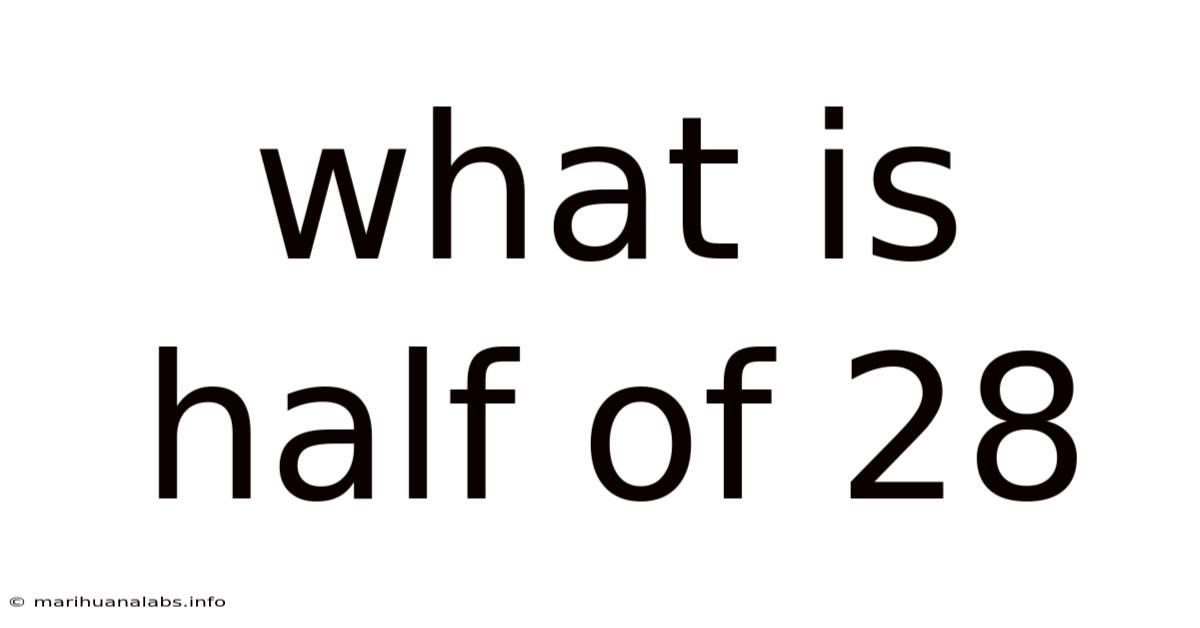
Table of Contents
What is Half of 28? A Deep Dive into Division and its Applications
Finding half of a number is a fundamental concept in mathematics, crucial for everyday life and advanced calculations. This seemingly simple question, "What is half of 28?", opens a door to exploring the broader world of division, fractions, percentages, and their practical applications. This article will not only answer the question directly but will also delve into the underlying mathematical principles, explore different methods for solving similar problems, and examine real-world scenarios where understanding halves is essential.
Understanding the Concept of Halving
The phrase "half of 28" implies dividing 28 into two equal parts. This is a basic division problem. Division is the inverse operation of multiplication; it involves splitting a quantity into a specified number of equal groups. In this case, we're splitting 28 into 2 equal groups.
The Answer: Half of 28 is 14. This can be represented mathematically as 28 ÷ 2 = 14, or as a fraction: 28/2 = 14.
Multiple Methods for Finding Half
While the answer is straightforward, let's explore several methods to arrive at the same solution. This will reinforce the understanding of the underlying mathematical principles and provide alternative approaches for similar problems.
-
Direct Division: This is the most common method. Simply divide 28 by 2 using long division or a calculator.
-
Fraction Representation: Expressing "half" as the fraction 1/2 allows us to solve the problem as a multiplication: (1/2) * 28 = 14. This approach highlights the relationship between fractions and division.
-
Repeated Subtraction: We can repeatedly subtract 2 from 28 until we reach 0. The number of times we subtract 2 represents half of 28. This method is less efficient for larger numbers but demonstrates the core concept of division.
-
Mental Math: With practice, we can quickly calculate half of many numbers mentally. Recognizing that 20 is half of 40 and 8 is half of 16, we can easily deduce that half of 28 (20 + 8) is 14 (10 + 4).
Beyond the Basics: Exploring Fractions and Percentages
Understanding halves is intrinsically linked to understanding fractions and percentages. "Half" represents 1/2, which is equivalent to 50%. This connection allows us to solve related problems. For instance:
-
What is 50% of 28? This is identical to finding half of 28, resulting in 14.
-
What is 25% of 28? Since 25% is half of 50%, we can find half of 14 (half of 28), which is 7.
-
What is 75% of 28? 75% is 3 times 25%, so we can multiply 7 (25% of 28) by 3, resulting in 21.
This demonstrates the interconnectedness of these mathematical concepts. Mastering the understanding of halves lays the groundwork for confidently tackling more complex percentage problems.
Real-World Applications of Halving
The concept of halving, seemingly simple, finds application in numerous real-world scenarios:
-
Sharing: Dividing resources equally amongst two people requires finding half. This is relevant for splitting bills, sharing food, or distributing tasks.
-
Cooking and Baking: Many recipes require halving or doubling ingredients. Understanding how to adjust recipes accurately is crucial for successful cooking.
-
Measurement and Construction: Measurements often involve halving lengths, distances, or volumes. This is crucial in construction, engineering, and design.
-
Financial Management: Budgeting often involves allocating half of income for essential expenses, allowing for better financial planning.
-
Data Analysis: In statistics and data analysis, calculating the median (middle value) of a dataset often involves identifying the halfway point.
-
Geometry and Spatial Reasoning: Calculating the area of triangles often involves understanding halves. The area of a triangle is half the base times the height.
-
Computer Science: In programming, particularly in algorithms and data structures, dividing problems into halves is a common technique for efficient problem-solving (e.g., binary search).
Extending the Concept: Halving Larger and Smaller Numbers
The principle of finding half applies to numbers of any size. Let's consider examples:
-
Halving larger numbers: To find half of 56, we can divide 56 by 2, resulting in 28. Similarly, half of 100 is 50, and half of 1000 is 500.
-
Halving decimals: The same principle applies to decimals. Half of 2.8 is 1.4. Half of 0.5 is 0.25.
-
Halving fractions: To find half of a fraction, we multiply the fraction by 1/2. For example, half of 1/4 is (1/2) * (1/4) = 1/8.
Addressing Potential Misconceptions
While finding half of 28 is straightforward, some misconceptions might arise when dealing with more complex numbers or scenarios.
-
Even vs. Odd Numbers: Halving even numbers always results in a whole number. However, halving odd numbers always results in a decimal or fraction (e.g., half of 27 is 13.5).
-
Negative Numbers: Halving a negative number results in a negative number. For instance, half of -28 is -14.
-
Zero: Half of zero is zero.
Understanding these nuances prevents errors in calculations and ensures accurate results.
Frequently Asked Questions (FAQ)
-
Q: What is the difference between halving and doubling?
- A: Halving divides a number by 2, while doubling multiplies a number by 2. They are inverse operations.
-
Q: How can I quickly calculate half of a number mentally?
- A: Practice recognizing patterns and breaking down numbers. For example, to find half of 74, think of it as half of 70 (35) plus half of 4 (2), resulting in 37.
-
Q: What if I need to find a third or a quarter of a number?
- A: To find a third, divide by 3. To find a quarter, divide by 4. These are extensions of the same principle of division.
-
Q: How does halving relate to other mathematical operations?
- A: Halving is directly related to division, fractions, percentages, and is fundamental to more advanced concepts in algebra, geometry, and calculus.
Conclusion
Finding half of 28, while a simple task, opens a gateway to a deeper understanding of fundamental mathematical concepts. From basic division to the complexities of fractions, percentages, and their real-world applications, this seemingly simple question reveals the interconnectedness of mathematical principles. By mastering the concept of halving, we build a strong foundation for tackling more complex mathematical problems and enhancing our ability to solve problems across various disciplines. The ability to easily calculate halves is not only a valuable skill for academic success but also a practical tool for everyday life, improving our ability to manage resources, make accurate calculations, and navigate various situations effectively.
Latest Posts
Latest Posts
-
What Is A Window Sill
Sep 09, 2025
-
D Major Scale In Piano
Sep 09, 2025
-
What Is 18km In Miles
Sep 09, 2025
-
Chords In D Major Scale
Sep 09, 2025
-
Quotes About Snowball Animal Farm
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is Half Of 28 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.