What Is 90 Of 15
marihuanalabs
Sep 20, 2025 · 6 min read
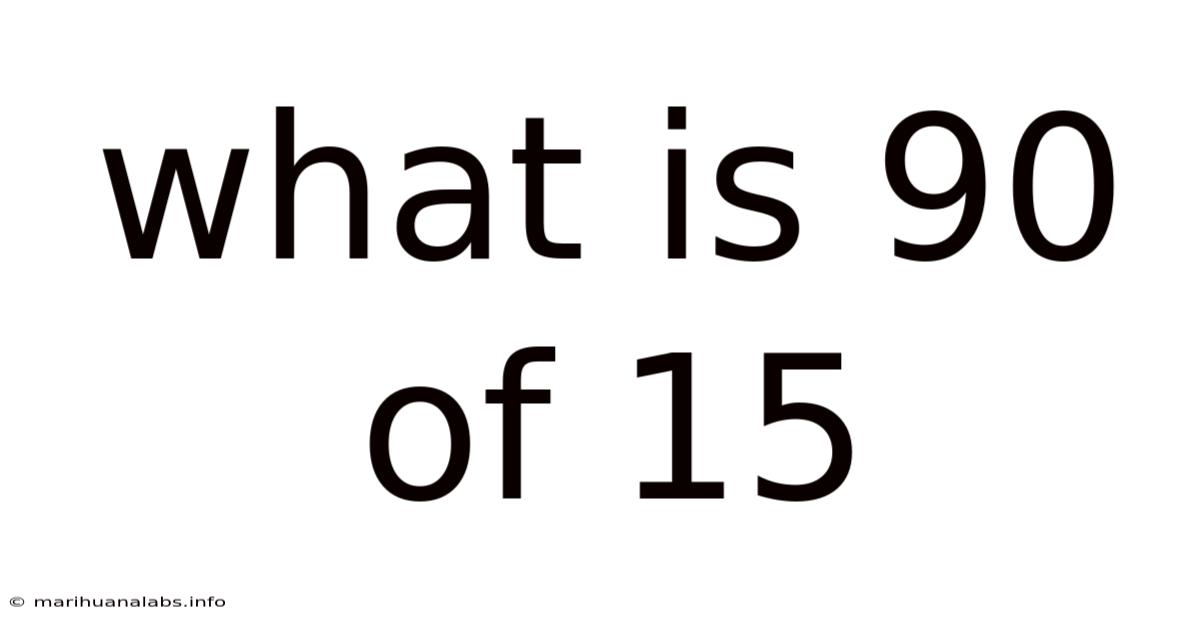
Table of Contents
What is 90% of 15? A Deep Dive into Percentages and Their Applications
Finding 90% of 15 might seem like a simple arithmetic problem, suitable only for elementary school. However, understanding how to calculate percentages, and the underlying principles involved, opens doors to a wide range of applications in various fields, from everyday budgeting to advanced statistical analysis. This article will not only solve the problem of "What is 90% of 15?" but will also explore the concept of percentages in detail, providing you with a robust understanding of this fundamental mathematical tool.
Understanding Percentages: The Foundation
A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of one hundred". Therefore, 90% can be written as 90/100 or as the decimal 0.9. Understanding this equivalence is crucial for performing percentage calculations.
The basic formula for calculating a percentage of a number is:
(Percentage/100) * Number = Result
In our case, the percentage is 90, and the number is 15. Let's apply the formula:
(90/100) * 15 = 13.5
Therefore, 90% of 15 is 13.5.
Different Methods to Calculate 90% of 15
While the formula above provides a direct and efficient method, there are other approaches to arrive at the same answer. Understanding these alternative methods can enhance your problem-solving skills and provide a deeper comprehension of percentages.
Method 1: Decimal Conversion
As mentioned earlier, 90% is equivalent to 0.9. Therefore, we can directly multiply 15 by 0.9:
15 * 0.9 = 13.5
This method is particularly useful when dealing with calculations involving a calculator, making it quick and straightforward.
Method 2: Fraction Conversion
90% can also be expressed as the fraction 90/100, which can be simplified to 9/10. Now, we can multiply 15 by 9/10:
15 * (9/10) = (15 * 9) / 10 = 135 / 10 = 13.5
This approach emphasizes the fractional nature of percentages and reinforces the understanding of equivalent fractions.
Method 3: Finding 10% and Scaling Up
This method utilizes the ease of calculating 10% of a number. 10% of 15 is simply 15/10 = 1.5. Since 90% is nine times 10%, we multiply 1.5 by 9:
1.5 * 9 = 13.5
This method is helpful for mental calculations and estimations, particularly when dealing with simpler percentages like 10%, 20%, 30%, etc.
Real-World Applications of Percentage Calculations
The seemingly simple calculation of finding 90% of 15 has far-reaching implications in various real-world scenarios. Let's explore a few examples:
-
Sales and Discounts: Imagine a store offering a 90% discount on an item priced at $15. The discounted price would be 90% of $15, which is $13.5. This is a common application of percentage calculations in retail and e-commerce.
-
Tax Calculations: Many countries impose sales tax on goods and services. If the sales tax rate is 90% (highly unlikely, but useful for illustrative purposes), the tax amount on a $15 item would be 90% of $15, or $13.5.
-
Financial Investments: Understanding percentages is essential when dealing with investments. Calculating returns on investments, interest rates, and growth often involves percentage calculations. For instance, if an investment grows by 90%, the growth on a $15 investment would be $13.5.
-
Statistical Analysis: Percentages are fundamental in statistical analysis. They are used to represent proportions, frequencies, and probabilities. Understanding percentages is critical for interpreting data and making informed decisions based on statistical findings.
-
Grading Systems: Many educational institutions use percentages to represent grades. A score of 90% on a 15-point quiz would translate to 13.5 points.
-
Surveys and Polling: Surveys and polls often express results in percentages. For example, 90% of respondents might agree with a particular statement. Understanding percentages is essential for correctly interpreting survey data.
-
Scientific Research: In many areas of scientific research, percentage calculations are frequently used to express experimental results, calculate statistical significance, or compare measurements between groups.
Beyond the Basics: More Complex Percentage Problems
While calculating 90% of 15 is relatively straightforward, more complex percentage problems require a deeper understanding of the underlying principles. Here are some examples:
-
Finding the original value: If you know that 90% of a number is 13.5, how do you find the original number? This requires reversing the percentage calculation. Divide 13.5 by 0.9 to find the original number (13.5 / 0.9 = 15).
-
Calculating percentage increase or decrease: If a value increases from 15 to 27, what is the percentage increase? First, find the difference (27 - 15 = 12). Then, divide the difference by the original value (12/15 = 0.8) and multiply by 100 to get the percentage increase (0.8 * 100 = 80%).
-
Calculating multiple percentages: What is 90% of 15, and then 20% of the result? This involves performing two sequential percentage calculations. First, calculate 90% of 15 (13.5). Then, calculate 20% of 13.5 (13.5 * 0.2 = 2.7).
These more complex problems illustrate that mastering percentage calculations opens the door to solving more intricate mathematical questions frequently encountered in various academic and professional settings.
Frequently Asked Questions (FAQ)
Q: Is there a quick way to calculate percentages in my head?
A: For some percentages, mental shortcuts can be useful. For instance, 10% is easily found by dividing by 10, 50% by dividing by 2, and 25% by dividing by 4. You can build from these basic percentages to calculate others. For example, 20% is double 10%, and 75% is three times 25%.
Q: What if I don't have a calculator?
A: You can always use the fractional method. Convert the percentage to a fraction and perform the multiplication. This often involves working with simpler fractions and can be done manually.
Q: Are there any online tools to help with percentage calculations?
A: Many websites and apps offer percentage calculators. These tools can be helpful for quick calculations or for checking your work. However, understanding the underlying principles is crucial for solving more complex problems.
Q: Why is understanding percentages important?
A: Percentages are a fundamental mathematical concept with widespread applications in numerous fields, making it essential for everyday life, academics, and professional success.
Conclusion
Calculating 90% of 15, while seemingly simple, serves as a gateway to understanding the broader concept of percentages and their pervasive role in our lives. From everyday transactions to complex financial models and scientific research, the ability to calculate and interpret percentages is a valuable skill that enhances problem-solving abilities and informs decision-making across various domains. This article aimed to not just provide the answer (13.5) but also equip you with the knowledge and skills to tackle a wide range of percentage-related problems confidently and efficiently. Remember, the key lies in understanding the underlying principles, not just memorizing formulas.
Latest Posts
Latest Posts
-
Scottish Widows Balanced Growth Portfolio
Sep 20, 2025
-
How To Find Yield Stress
Sep 20, 2025
-
How Much Is 40 Oz
Sep 20, 2025
-
Barium Hydroxide And Hydrochloric Acid
Sep 20, 2025
-
Number Of Protons In Xenon
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 90 Of 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.