What Is 80 Of 25
marihuanalabs
Sep 20, 2025 · 5 min read
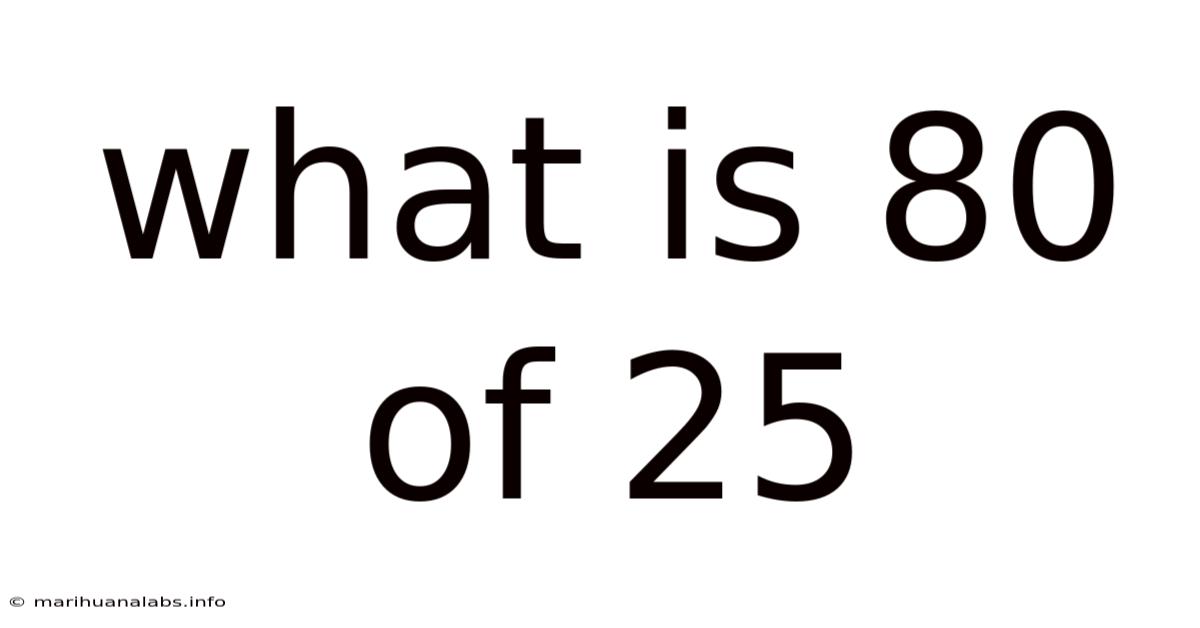
Table of Contents
What is 80% of 25? A Deep Dive into Percentages and Their Applications
Finding 80% of 25 might seem like a simple arithmetic problem, but it opens the door to understanding a fundamental concept in mathematics and its wide-ranging applications in everyday life. This article will not only show you how to calculate 80% of 25 but also delve into the underlying principles of percentages, exploring different calculation methods and showcasing their relevance in various fields. We’ll even tackle some common misconceptions and frequently asked questions. By the end, you’ll have a solid grasp of percentages and be able to confidently tackle similar problems.
Understanding Percentages:
Before we jump into the calculation, let's clarify what a percentage actually is. A percentage is a fraction or a ratio expressed as a number out of 100. The word "percent" literally means "out of one hundred" ("per cent" in Latin). So, 80% means 80 out of 100, which can be written as the fraction 80/100 or the decimal 0.8.
Method 1: Using the Decimal Equivalent
This is perhaps the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the number.
-
Step 1: Convert the percentage to a decimal: To convert 80% to a decimal, we divide 80 by 100: 80 ÷ 100 = 0.8
-
Step 2: Multiply the decimal by the number: Now, we multiply the decimal (0.8) by the number we want to find the percentage of (25): 0.8 x 25 = 20
Therefore, 80% of 25 is $\boxed{20}$.
Method 2: Using the Fraction Equivalent
We can also solve this problem using fractions.
-
Step 1: Convert the percentage to a fraction: 80% can be written as the fraction 80/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 20: 80/100 = 4/5
-
Step 2: Multiply the fraction by the number: Now, we multiply the simplified fraction (4/5) by 25: (4/5) x 25 = (4 x 25) / 5 = 100 / 5 = 20
Again, we arrive at the answer: 80% of 25 is $\boxed{20}$.
Method 3: Using Proportions
This method is particularly useful for understanding the underlying relationship between percentages and proportions. We can set up a proportion to solve for the unknown value.
-
Step 1: Set up a proportion: We can express the problem as a proportion: 80/100 = x/25, where 'x' represents the value we want to find (80% of 25).
-
Step 2: Cross-multiply: To solve for 'x', we cross-multiply: 80 x 25 = 100 x x
-
Step 3: Solve for x: This simplifies to 2000 = 100x. Dividing both sides by 100, we get x = 20.
So, once again, 80% of 25 is $\boxed{20}$.
Real-World Applications of Percentages:
Understanding percentages is crucial in many aspects of daily life and various professions. Here are a few examples:
-
Sales and Discounts: Stores frequently advertise discounts as percentages. For example, a "20% off" sale means you pay 80% of the original price. Calculating percentages helps determine the final price after a discount.
-
Finance and Investments: Percentages are fundamental in finance. Interest rates on loans and savings accounts are expressed as percentages. Calculating percentage returns on investments is crucial for assessing financial performance.
-
Statistics and Data Analysis: Percentages are essential for representing data in a clear and concise manner. For example, survey results are often presented as percentages to show the proportion of respondents who chose a particular option. Understanding percentages is key to interpreting statistical data.
-
Science and Engineering: Percentages are used extensively in scientific calculations and engineering designs. For example, expressing the efficiency of a machine or the concentration of a solution as a percentage.
-
Everyday Life: We encounter percentages in various everyday situations. Calculating tips in restaurants, understanding tax rates, or determining the percentage of completion of a project all involve using percentages.
Common Misconceptions about Percentages:
-
Adding Percentages: It’s important to remember that you cannot simply add percentages together unless they are applied to the same base value. For example, a 10% increase followed by a 10% decrease does not result in the original value; it results in a slight decrease.
-
Percentage Change: Calculating percentage change requires careful consideration of the initial and final values. The formula for percentage change is: [(Final Value - Initial Value) / Initial Value] x 100.
-
Percentage Points: A percentage point is a unit of measure representing the absolute difference between two percentages. For example, an increase from 20% to 25% is a five percentage point increase, not a 25% increase.
Frequently Asked Questions (FAQ):
- Q: How do I calculate a percentage of a number mentally?
A: For simple percentages like 10%, 20%, 50%, etc., you can often calculate them mentally using simple fractions. For example, 10% is 1/10, so 10% of 25 is 25/10 = 2.5. For more complex percentages, using the decimal method is often easier.
- Q: What if I need to calculate a percentage that isn't a whole number, such as 7.5%?
A: You use the same methods but with the decimal equivalent of 7.5%, which is 0.075. Multiply 0.075 by the number to find the percentage.
- Q: Can I use a calculator to calculate percentages?
A: Absolutely! Most calculators have a percentage button (%) that simplifies the calculation. You would enter the number, then the percentage, then the % button, and the calculator will perform the calculation.
- Q: Are there any online tools or software that can help calculate percentages?
A: Yes, many online calculators and spreadsheet software (like Microsoft Excel or Google Sheets) have built-in functions to easily calculate percentages.
Conclusion:
Calculating 80% of 25, while seemingly simple, provides a gateway to understanding the versatile and indispensable concept of percentages. From everyday transactions to complex financial models and scientific analyses, percentages play a critical role. Mastering percentage calculations is a valuable skill that enhances problem-solving abilities and improves comprehension in a wide range of fields. By understanding the different methods—decimal conversion, fraction conversion, and proportions—you can confidently tackle any percentage calculation and apply this fundamental mathematical concept effectively in various aspects of your life. Remember to always double-check your work and be mindful of common misconceptions to ensure accuracy in your calculations.
Latest Posts
Latest Posts
-
How To Work Out Mr
Sep 20, 2025
-
How Long Is 39 Inches
Sep 20, 2025
-
Mythical Animals List With Pictures
Sep 20, 2025
-
1 Teaspoon Yeast To Grams
Sep 20, 2025
-
Market Mapping Advantages And Disadvantages
Sep 20, 2025
Related Post
Thank you for visiting our website which covers about What Is 80 Of 25 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.