What Is 75 Of 40
marihuanalabs
Sep 15, 2025 · 6 min read
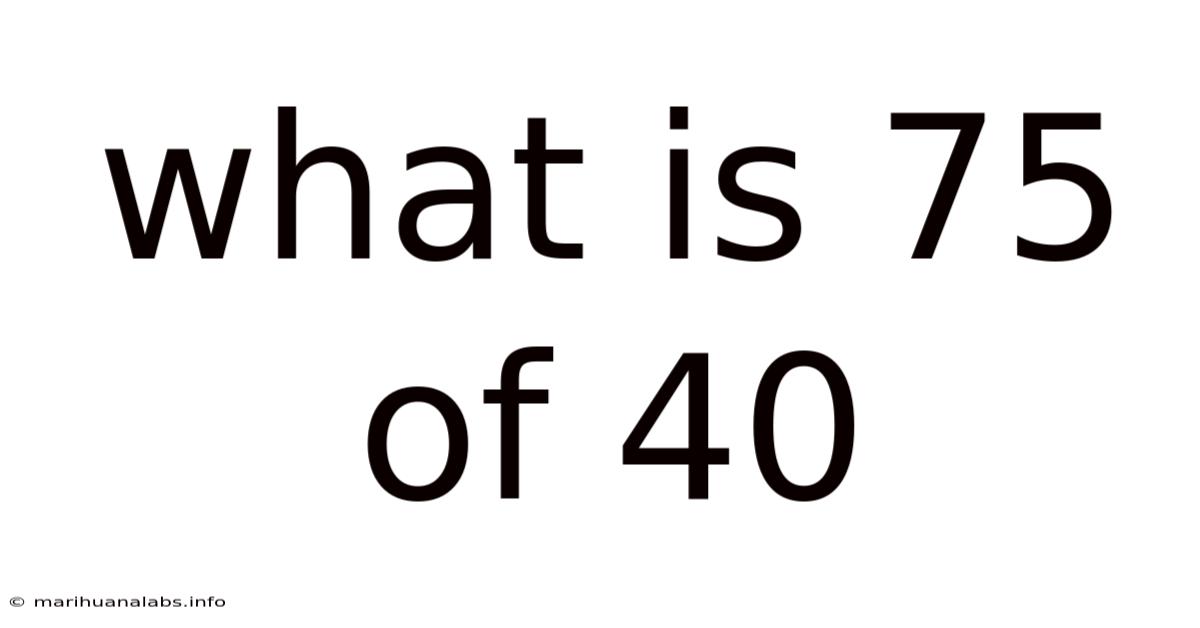
Table of Contents
What is 75% of 40? A Deep Dive into Percentages and Their Applications
Finding 75% of 40 might seem like a simple arithmetic problem, easily solvable with a calculator. However, understanding the underlying principles of percentages goes far beyond simple calculations. This article will not only answer the question "What is 75% of 40?" but also delve into the fundamental concepts of percentages, exploring different calculation methods, real-world applications, and addressing common misconceptions. This comprehensive guide will equip you with the knowledge to confidently tackle percentage problems of any complexity.
Understanding Percentages: The Basics
A percentage is a way of expressing a number as a fraction of 100. The word "percent" literally means "out of one hundred" ( per centum in Latin). Therefore, 75% means 75 out of 100, or 75/100. This fraction can be simplified to 3/4. Understanding this fundamental concept is crucial for grasping percentage calculations.
Calculating 75% of 40: Method 1 - Using Fractions
The most straightforward method to calculate 75% of 40 involves converting the percentage to a fraction and then multiplying. As mentioned earlier, 75% is equivalent to 3/4. Therefore, the calculation becomes:
(3/4) * 40 = 30
This method is particularly useful when dealing with percentages that have easy fractional equivalents, like 25%, 50%, and 75%.
Calculating 75% of 40: Method 2 - Using Decimals
Another common method involves converting the percentage to a decimal. To convert a percentage to a decimal, divide the percentage by 100. In this case:
75% / 100 = 0.75
Then, multiply the decimal by the number:
0.75 * 40 = 30
This method is generally preferred when dealing with percentages that don't have simple fractional equivalents. It's also easily adaptable for use with calculators.
Calculating 75% of 40: Method 3 - Using Proportions
The proportion method offers a more visual and intuitive approach to solving percentage problems. A proportion sets up an equivalence between two ratios. We can set up the proportion as follows:
75/100 = x/40
Where 'x' represents the unknown value (75% of 40). To solve for 'x', we cross-multiply:
75 * 40 = 100 * x
3000 = 100x
x = 3000 / 100
x = 30
This method is particularly helpful for visualizing the relationship between the percentage and the whole number. It also provides a systematic approach that can be applied to more complex percentage problems.
Real-World Applications of Percentage Calculations
Understanding percentages is crucial in numerous aspects of daily life and professional fields. Here are a few examples:
-
Sales and Discounts: Calculating discounts on items during sales is a common application. For example, a 25% discount on a $100 item means a saving of $25 (25% of $100).
-
Taxes: Sales tax, income tax, and other taxes are expressed as percentages. Calculating the tax amount on a purchase or income requires understanding percentage calculations.
-
Interest Rates: Interest rates on loans, savings accounts, and investments are expressed as percentages. Understanding these percentages is crucial for making informed financial decisions.
-
Statistics and Data Analysis: Percentages are frequently used to represent proportions and trends in data. For example, the unemployment rate, crime rates, and survey results are often expressed as percentages.
-
Science and Engineering: Percentages are used extensively in scientific calculations and engineering designs. For example, calculating the efficiency of a machine or the concentration of a solution often involves percentage calculations.
-
Healthcare: In medicine, dosages of medication are often calculated as percentages of a patient's body weight or blood volume.
Common Misconceptions about Percentages
Several common misconceptions surround percentage calculations. Let's address some of them:
-
Adding Percentages Directly: You cannot simply add percentages directly without considering the base value. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Confusing Percentage Change with Percentage Points: A change from 10% to 20% is a 10 percentage point increase, but a 100% increase in the percentage. This distinction is crucial in understanding statistical data.
-
Incorrectly Calculating Percentage Increases and Decreases: Calculating percentage increases and decreases requires careful consideration of the base value. A common mistake is to calculate the percentage change based on the incorrect value.
-
Misinterpreting Percentage Points: It's vital to distinguish between percentage points and percentage changes. For example, an increase from 5% to 10% represents a 5 percentage point increase, but a 100% increase in the percentage itself.
Advanced Percentage Calculations: Beyond the Basics
While finding 75% of 40 is a relatively simple calculation, more complex scenarios may arise. Here are a few examples:
-
Finding the original value after a percentage increase or decrease: If an item costs $60 after a 20% increase, you need to work backward to determine the original price. This involves using algebraic equations.
-
Calculating multiple percentage changes: Determining the final value after consecutive percentage changes requires a step-by-step approach, applying each percentage change to the preceding result.
-
Calculating percentages with complex fractions: Problems involving complex fractions or decimals may require a more systematic approach using the decimal or proportion methods.
-
Applying percentages to real-world problems: Many real-world problems involve combining percentage calculations with other mathematical concepts, such as ratios, proportions, and rates.
Frequently Asked Questions (FAQ)
Q: How do I calculate a percentage of a number quickly in my head?
A: For common percentages like 10%, 25%, 50%, and 75%, mental calculation is often easier by using the corresponding fraction equivalents. For example, 10% is 1/10, so 10% of 40 is 40/10 = 4. Practice will improve your mental math skills.
Q: What is the difference between percentage increase and percentage decrease?
A: A percentage increase refers to the relative increase of a value, while a percentage decrease represents the relative decrease of a value, both expressed as a percentage of the original value.
Q: How can I check my percentage calculations?
A: The best way to check your calculation is to use a different method (e.g., if you used the decimal method, try using the fraction method). You can also use an online calculator to verify your answer.
Conclusion
Calculating 75% of 40, as we've demonstrated, results in 30. However, the true value of understanding percentages lies in its broad applicability across various disciplines and everyday scenarios. Mastering percentage calculations empowers you to make informed decisions in finance, shopping, data interpretation, and more. While this article provides a comprehensive overview, further exploration and practice are encouraged to solidify your understanding and build confidence in tackling complex percentage problems. Remember to always focus on understanding the fundamental concepts and choose the calculation method that best suits your needs and the complexity of the problem. By applying these principles, you'll navigate the world of percentages with ease and precision.
Latest Posts
Latest Posts
-
A Conversation With Oscar Wilde
Sep 15, 2025
-
Point Of Care Testing Devices
Sep 15, 2025
-
Difference Between Burglary And Theft
Sep 15, 2025
-
Themes In Death Of Salesman
Sep 15, 2025
-
What Is The Standard Solution
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 75 Of 40 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.