What Is 60 Of 80
marihuanalabs
Sep 11, 2025 · 5 min read
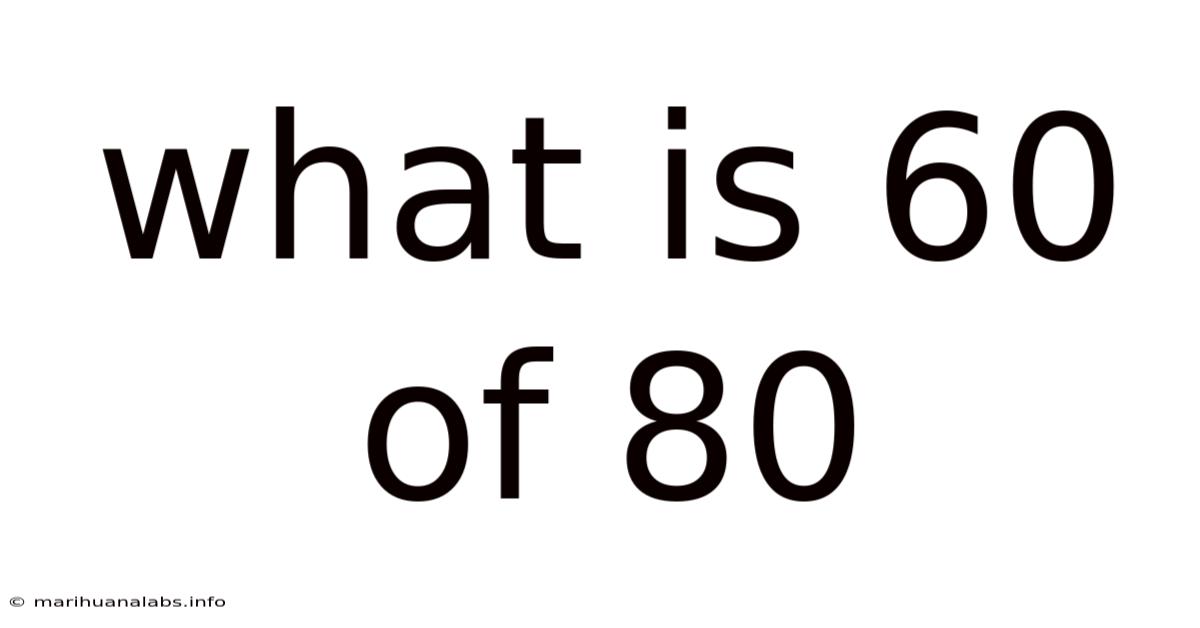
Table of Contents
What is 60% of 80? A Comprehensive Guide to Percentages and Their Applications
Finding 60% of 80 might seem like a simple calculation, but understanding the underlying principles of percentages is crucial for various aspects of life, from everyday budgeting to complex financial analysis. This comprehensive guide will not only show you how to calculate 60% of 80 but also delve into the broader world of percentages, exploring different calculation methods, real-world applications, and frequently asked questions. By the end, you'll be well-equipped to tackle percentage problems with confidence.
Understanding Percentages: The Basics
A percentage is a fraction or a ratio expressed as a number out of 100. The word "percent" literally means "per hundred." So, 60% means 60 out of 100, which can be written as the fraction 60/100 or the decimal 0.60. This representation is key to understanding how percentages work.
Calculating 60% of 80: Three Methods
There are several ways to calculate 60% of 80. Let's explore three common methods:
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage to its decimal equivalent and then multiply it by the number.
- Step 1: Convert the percentage to a decimal: 60% = 60/100 = 0.60
- Step 2: Multiply the decimal by the number: 0.60 * 80 = 48
Therefore, 60% of 80 is 48.
Method 2: Using the Fraction Equivalent
This method involves converting the percentage to a fraction and then performing the multiplication.
- Step 1: Convert the percentage to a fraction: 60% = 60/100
- Step 2: Simplify the fraction (if possible): 60/100 simplifies to 3/5
- Step 3: Multiply the fraction by the number: (3/5) * 80 = (3 * 80) / 5 = 240 / 5 = 48
Again, 60% of 80 is 48.
Method 3: Using Proportions
This method utilizes the concept of ratios and proportions. We set up a proportion where we know three values and solve for the unknown.
- Step 1: Set up the proportion: 60/100 = x/80 (where x represents 60% of 80)
- Step 2: Cross-multiply: 60 * 80 = 100 * x
- Step 3: Solve for x: 4800 = 100x => x = 4800 / 100 = 48
Once again, we find that 60% of 80 is 48.
Real-World Applications of Percentages
Understanding percentages is essential in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, taxes, profits, and losses all rely heavily on percentages. For example, figuring out the interest earned on a savings account or the discount on a sale item requires a solid grasp of percentage calculations.
-
Statistics: Percentages are fundamental to interpreting and presenting statistical data. Understanding the percentage change in a population, the percentage of people who voted for a particular candidate, or the percentage of students who passed an exam all require proficiency in percentage calculations.
-
Science: In scientific research, percentages are often used to express the concentration of a substance in a solution, the percentage error in an experiment, or the percentage of a population exhibiting a particular trait.
-
Everyday Life: From calculating tips in restaurants to understanding sales tax or determining the percentage of completion on a project, percentages are interwoven into our daily routines.
Beyond the Basics: Advanced Percentage Calculations
While finding 60% of 80 is a straightforward calculation, more complex scenarios may arise:
-
Finding the percentage one number represents of another: For example, what percentage of 80 is 48? This involves dividing the smaller number (48) by the larger number (80) and multiplying by 100: (48/80) * 100 = 60%.
-
Calculating percentage increase or decrease: This involves determining the difference between two numbers and expressing that difference as a percentage of the original number. For instance, if a price increases from $80 to $100, the percentage increase is calculated as: (($100 - $80) / $80) * 100 = 25%.
-
Working with multiple percentages: Sometimes you need to apply multiple percentages sequentially. For example, finding the final price after applying a 10% discount followed by a 5% sales tax requires careful step-by-step calculations.
-
Solving for an unknown percentage: In some cases, you'll know the result and one of the numbers, and you need to find the percentage. For instance, if 24 represents x% of 80, you'd solve for x as follows: (24/80) * 100 = 30%.
Understanding Percentage Change: A Deeper Dive
Calculating percentage change is particularly important when analyzing trends and comparing data over time. There are two main types of percentage change:
-
Percentage Increase: Calculated as [(New Value - Old Value) / Old Value] * 100. A positive result indicates an increase.
-
Percentage Decrease: Calculated as [(Old Value - New Value) / Old Value] * 100. A positive result indicates a decrease. Note that this formula yields a positive value for a decrease.
Frequently Asked Questions (FAQ)
Q1: How can I quickly calculate percentages in my head?
A1: For common percentages like 10%, 20%, 50%, etc., you can often perform quick mental calculations. 10% is simply one-tenth, 20% is one-fifth, and 50% is one-half. For other percentages, rounding to the nearest 10% or 25% can provide a good estimate.
Q2: What are some common mistakes to avoid when calculating percentages?
A2: Common mistakes include incorrect decimal conversion, forgetting to multiply by 100 when calculating percentages, and misinterpreting percentage increase or decrease calculations. Always double-check your work and ensure you understand the context of the problem.
Q3: Are there any online tools or calculators that can help with percentage calculations?
A3: Many online calculators are available to perform percentage calculations. These can be helpful for checking your work or for more complex calculations. However, understanding the underlying principles remains crucial.
Q4: How can I improve my understanding of percentages?
A4: Practice is key. Work through various percentage problems, starting with simpler examples and gradually progressing to more complex ones. Understanding the different methods for calculating percentages will strengthen your skills.
Conclusion
Calculating 60% of 80, which equals 48, is a fundamental percentage calculation. However, this seemingly simple problem opens the door to understanding a much broader concept with vast applications across numerous fields. Mastering percentages empowers you to interpret data effectively, make informed decisions in finance, and navigate everyday situations more confidently. By understanding the different methods and their applications, you can build a strong foundation for tackling more complex percentage problems and confidently navigating the world of numbers. Remember to practice regularly to solidify your understanding and enhance your problem-solving skills.
Latest Posts
Latest Posts
-
Pillars Of The Earth Cast
Sep 11, 2025
-
7 Out Of 20 Percentage
Sep 11, 2025
-
What Is A Reaction Profile
Sep 11, 2025
-
Grammar Capital Letter After Colon
Sep 11, 2025
-
Example Of A Narrative Observation
Sep 11, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Of 80 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.