What Is 5 Of 30
marihuanalabs
Sep 23, 2025 · 5 min read
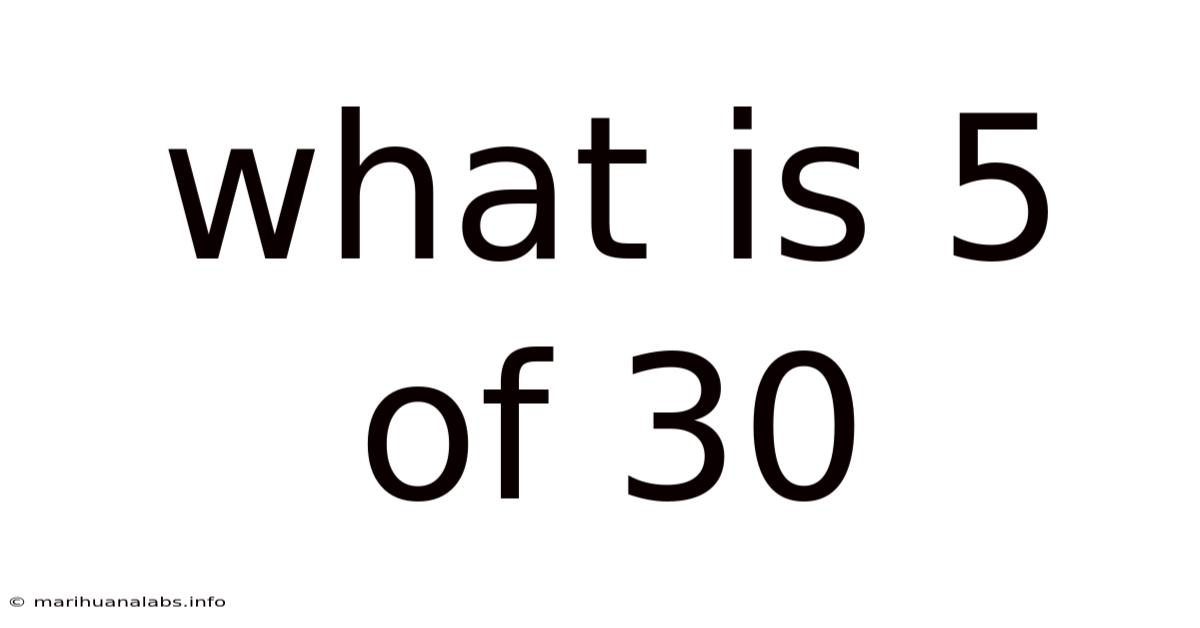
Table of Contents
What is 5 of 30? Understanding Fractions, Percentages, and Ratios
This article delves into the seemingly simple question: "What is 5 of 30?" While the immediate answer might appear straightforward, exploring this question opens the door to understanding fundamental mathematical concepts like fractions, percentages, and ratios. We'll unpack these concepts, providing clear explanations and practical examples to solidify your grasp of these essential building blocks of mathematics.
Introduction: Deconstructing "5 of 30"
The phrase "5 of 30" implies a part-to-whole relationship. It signifies a portion (5) out of a larger total (30). This relationship can be expressed in several ways: as a fraction, a percentage, or a ratio. Each representation provides a different perspective on the same underlying relationship. This article will explore each of these representations and their practical applications.
1. Understanding Fractions: Representing Parts of a Whole
A fraction is a numerical representation of a part of a whole. It consists of two numbers: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of parts being considered, while the denominator represents the total number of equal parts that make up the whole.
In the case of "5 of 30," the fraction is written as 5/30. Here, 5 is the numerator (the number of parts we're interested in), and 30 is the denominator (the total number of parts).
-
Simplifying Fractions: The fraction 5/30 can be simplified. Simplification involves finding the greatest common divisor (GCD) of both the numerator and denominator and dividing both by that number. The GCD of 5 and 30 is 5. Dividing both the numerator and the denominator by 5, we get:
5/30 = 1/6
This simplified fraction, 1/6, represents the same proportion as 5/30 but in its simplest form. It means that 5 out of 30 is equivalent to 1 out of 6.
2. Converting Fractions to Percentages: Expressing Proportion as a Rate
A percentage is a way of expressing a proportion as a rate per hundred. To convert a fraction to a percentage, we first convert the fraction to a decimal by dividing the numerator by the denominator. Then, we multiply the decimal by 100 and add the "%" symbol.
Let's convert 5/30 (or its simplified form, 1/6) to a percentage:
-
Decimal Conversion: 1 ÷ 6 ≈ 0.1667
-
Percentage Conversion: 0.1667 x 100 ≈ 16.67%
Therefore, 5 out of 30 represents approximately 16.67%. This means that 5 is approximately 16.67% of 30.
3. Understanding Ratios: Comparing Two Quantities
A ratio compares two or more quantities. It shows the relative sizes of the quantities. The ratio of 5 to 30 is written as 5:30 or 5/30. Similar to fractions, ratios can be simplified by finding the greatest common divisor and dividing both quantities by it.
The simplified ratio of 5:30 is 1:6. This means that for every 1 part of one quantity, there are 6 parts of the other quantity.
4. Practical Applications: Real-world Scenarios
Understanding fractions, percentages, and ratios is crucial in various real-world situations. Here are a few examples illustrating the application of "5 of 30":
-
Test Scores: If a student answers 5 questions correctly out of a total of 30 questions on a test, their score is 5/30 or 1/6, which is approximately 16.67%.
-
Inventory Management: If a store has 30 units of a particular item and 5 are sold, 5/30 or 1/6 (approximately 16.67%) of the inventory has been sold.
-
Survey Results: If 5 out of 30 people surveyed prefer a particular product, then 5/30 or 1/6 (approximately 16.67%) of the respondents prefer that product.
-
Recipe Scaling: If a recipe calls for 30 grams of flour and you want to reduce it to 5 grams, you're using 5/30 or 1/6 of the original amount.
5. Further Exploring Proportions: Extending the Concept
The concept of "5 of 30" extends beyond simple fractions, percentages, and ratios. It can be used to solve more complex proportion problems. For example, you might want to find out how many items would be represented by 15% if the total is still 30. Setting up a proportion:
5/30 = x/100
Solving for x, we get:
x = (5 * 100) / 30 = 16.67 (approximately)
This means that 16.67 is approximately 5/30 expressed as a percentage. This reinforces the idea of proportion and highlights the interconnectedness of fractions, percentages, and ratios.
6. Advanced Concepts: Connecting to Algebra
The concept of "5 of 30" lays a foundation for more advanced mathematical concepts. For example, it can be expressed as an algebraic equation:
x/30 = 5/30
Solving for x, we confirm that x = 5. This simple equation introduces the power of algebraic representation and problem-solving. This simple example can be expanded to solve for unknown quantities in more complex scenarios involving proportions and percentages. For instance, if we know that 15% of a quantity is 5, we can set up an equation to find the total quantity.
7. Frequently Asked Questions (FAQ)
-
Q: What is the difference between a fraction, a percentage, and a ratio?
- A: A fraction represents a part of a whole. A percentage expresses a proportion as a rate per hundred. A ratio compares two or more quantities. While they represent similar concepts, they offer different ways of expressing proportional relationships.
-
Q: Can I simplify any fraction?
- A: Yes, any fraction can be simplified as long as the numerator and denominator share a common divisor greater than 1. If their greatest common divisor is 1, the fraction is already in its simplest form.
-
Q: Why is it important to simplify fractions?
- A: Simplifying fractions makes them easier to understand and work with. It also helps to identify the essential proportional relationship.
8. Conclusion: Mastering Fundamental Mathematical Concepts
Understanding "5 of 30" is not merely about finding a numerical answer. It's about grasping the fundamental concepts of fractions, percentages, and ratios. These concepts are the building blocks of more advanced mathematics and are widely applicable in everyday life. By understanding these relationships, you develop a stronger mathematical foundation, enabling you to solve complex problems and make informed decisions in various fields. The seemingly simple question of "What is 5 of 30?" becomes a gateway to a deeper understanding of mathematical proportions and their real-world applications. Mastering these concepts empowers you to navigate the quantitative aspects of life with confidence and precision.
Latest Posts
Latest Posts
-
Heaviest Organ Of Human Body
Sep 23, 2025
-
The King In Yellow 40k
Sep 23, 2025
-
First 5 Multiples Of 7
Sep 23, 2025
-
24 Is A Multiple Of
Sep 23, 2025
-
Script Much Ado About Nothing
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Of 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.