What Is 5 Of 20
marihuanalabs
Sep 08, 2025 · 6 min read
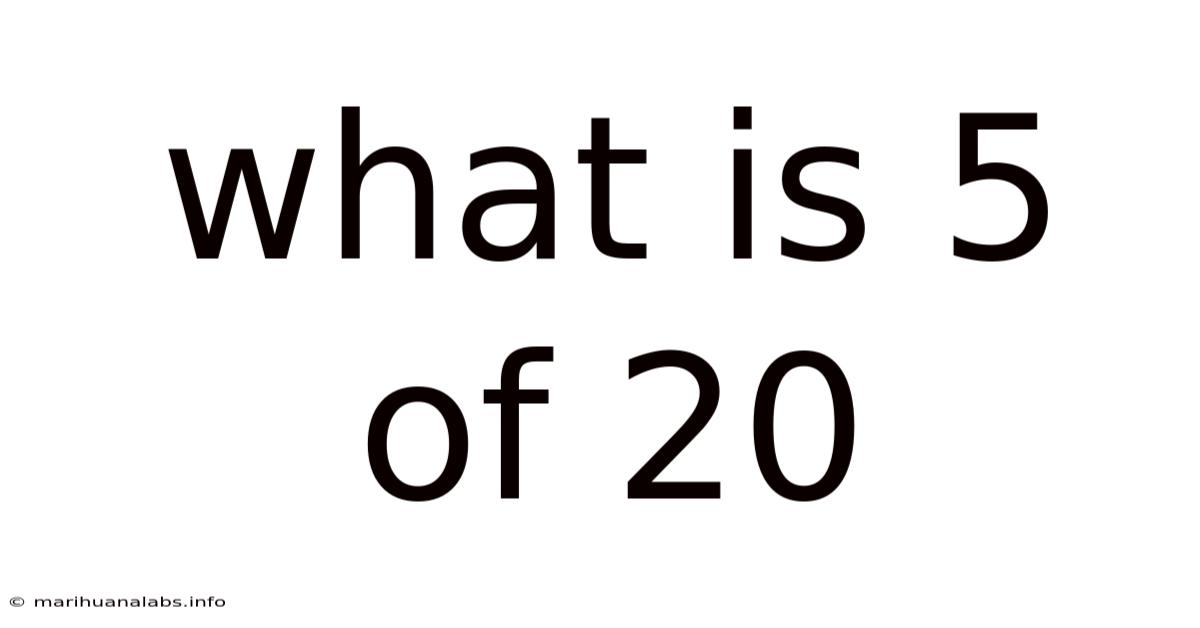
Table of Contents
What is 5 of 20? Understanding Fractions, Percentages, and Ratios
This article delves into the seemingly simple question, "What is 5 of 20?" While the answer might seem immediately obvious to some, understanding this question fully opens the door to a broader comprehension of fundamental mathematical concepts like fractions, percentages, and ratios. We'll explore these concepts in detail, providing a thorough explanation suitable for learners of all levels. This exploration will go beyond a simple numerical answer, highlighting the practical applications and real-world relevance of these mathematical tools.
Understanding the Basic Calculation
At its core, "5 of 20" implies a portion or part of a larger whole. The simplest interpretation is a fraction: 5 out of 20. This can be expressed mathematically as 5/20. To understand the relationship between 5 and 20, we can simplify this fraction by finding the greatest common divisor (GCD) of both numbers. The GCD of 5 and 20 is 5. Dividing both the numerator (5) and the denominator (20) by 5, we get the simplified fraction 1/4.
Therefore, 5 of 20 is equivalent to 1/4, or one-quarter. This means that 5 represents one-fourth of the total value of 20.
Exploring Fractions: A Deeper Dive
Fractions are a fundamental building block of mathematics. They represent a part of a whole, where the numerator (the top number) indicates the number of parts you have, and the denominator (the bottom number) indicates the total number of parts the whole is divided into. In our example, 5/20, 5 is the numerator and 20 is the denominator.
Understanding fractions is crucial for numerous applications:
- Everyday life: Dividing a pizza among friends, sharing sweets, or measuring ingredients for a recipe all involve fractions.
- Cooking and baking: Precise measurements often necessitate fractions, ensuring consistent results.
- Construction and engineering: Blueprints and design specifications frequently use fractions to specify dimensions and proportions.
- Finance: Understanding interest rates, loan repayments, and stock market fluctuations often requires working with fractions and percentages.
Converting Fractions to Percentages and Decimals
The fraction 1/4 (or 5/20) can be easily converted into a percentage and a decimal. To convert a fraction to a percentage, we multiply the fraction by 100%.
(1/4) * 100% = 25%
Therefore, 5 of 20 is 25% of the whole. This means that 5 represents 25% of the total value of 20.
To convert the fraction to a decimal, we simply divide the numerator by the denominator:
1 ÷ 4 = 0.25
So, 5 of 20 is also equal to 0.25.
Introducing Ratios: Another Perspective
The relationship between 5 and 20 can also be expressed as a ratio. A ratio compares two or more quantities. In this case, the ratio of 5 to 20 is written as 5:20. Like fractions, ratios can be simplified by finding the greatest common divisor. Simplifying the ratio 5:20, we get the equivalent ratio 1:4. This ratio indicates that for every one part, there are four parts in total.
Ratios are used extensively in:
- Scaling and proportions: Enlarging or reducing images, maps, or blueprints involves using ratios.
- Mixing ingredients: Recipes often specify ingredient ratios to ensure the desired outcome.
- Comparing quantities: Analyzing sales data, comparing population densities, or evaluating the performance of different investments can all involve using ratios.
Real-World Applications of Fractions, Percentages, and Ratios
The concepts of fractions, percentages, and ratios are interwoven and essential for understanding and solving various real-world problems. Here are some examples:
- Sales and discounts: A store offering a 25% discount on an item is essentially applying the fraction 1/4 (or the decimal 0.25) to the original price.
- Surveys and statistics: Representing survey results often involves percentages, allowing for easy comparison and analysis of different groups.
- Financial planning: Calculating interest earned on savings, determining loan repayments, or budgeting for expenses all involve working with fractions, decimals, and percentages.
- Data analysis: Ratios are used extensively in analyzing data to identify trends, make comparisons, and draw meaningful conclusions. For example, the debt-to-equity ratio in finance is a crucial metric for evaluating a company’s financial health.
Problem-Solving with Fractions, Percentages, and Ratios
Let’s explore some practical examples to solidify our understanding:
Example 1: A class has 20 students, and 5 of them are girls. What percentage of the class are girls?
This is simply calculating 5/20, which simplifies to 1/4, or 25%. Therefore, 25% of the class are girls.
Example 2: A recipe calls for a 1:4 ratio of sugar to flour. If you use 100 grams of sugar, how much flour should you use?
The ratio 1:4 means that for every 1 part of sugar, you need 4 parts of flour. If you have 100 grams of sugar (1 part), you need 4 * 100 = 400 grams of flour (4 parts).
Example 3: A store is selling a TV for $400, but offers a 15% discount. What is the discounted price?
First, calculate the discount amount: 15% of $400 = 0.15 * $400 = $60. Then, subtract the discount from the original price: $400 - $60 = $340. The discounted price is $340.
Further Exploration and Advanced Concepts
While this article provides a fundamental understanding of "5 of 20" and the associated mathematical concepts, there are many more advanced topics to explore. These include:
- Complex fractions: Fractions within fractions, requiring a deeper understanding of mathematical operations.
- Algebraic fractions: Fractions involving variables, requiring algebraic manipulation to simplify and solve equations.
- Proportionality and inverse proportionality: Understanding how changes in one quantity affect another quantity.
- Statistical applications: Using fractions, percentages, and ratios in statistical analysis to interpret data and make predictions.
Frequently Asked Questions (FAQ)
Q: What is the simplest form of the fraction 5/20?
A: The simplest form is 1/4.
Q: How do I convert a fraction to a decimal?
A: Divide the numerator by the denominator.
Q: How do I convert a fraction to a percentage?
A: Multiply the fraction by 100%.
Q: What is the difference between a ratio and a fraction?
A: While both compare quantities, a fraction represents a part of a whole, while a ratio compares two or more quantities. They are closely related and often interchangeable in many applications.
Q: Can a ratio be expressed as a fraction?
A: Yes, a ratio can be directly expressed as a fraction. For example, the ratio 1:4 can be expressed as the fraction 1/4.
Conclusion
Understanding "5 of 20" is more than just a simple calculation; it's a gateway to grasping the fundamental concepts of fractions, percentages, and ratios. These mathematical tools are indispensable in various aspects of life, from everyday tasks to complex problem-solving in professional fields. By understanding these concepts, we are equipped to navigate a vast range of situations and challenges effectively. This article serves as a stepping stone for further exploration into the fascinating world of mathematics and its practical applications. Continue to explore these concepts and build a stronger foundation in mathematical literacy, unlocking a deeper understanding of the world around you.
Latest Posts
Latest Posts
-
D Major Scale In Piano
Sep 09, 2025
-
What Is 18km In Miles
Sep 09, 2025
-
Chords In D Major Scale
Sep 09, 2025
-
Quotes About Snowball Animal Farm
Sep 09, 2025
-
Duchess Of Malfi Plot Summary
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.