What Is 5 / 0
marihuanalabs
Sep 19, 2025 · 7 min read
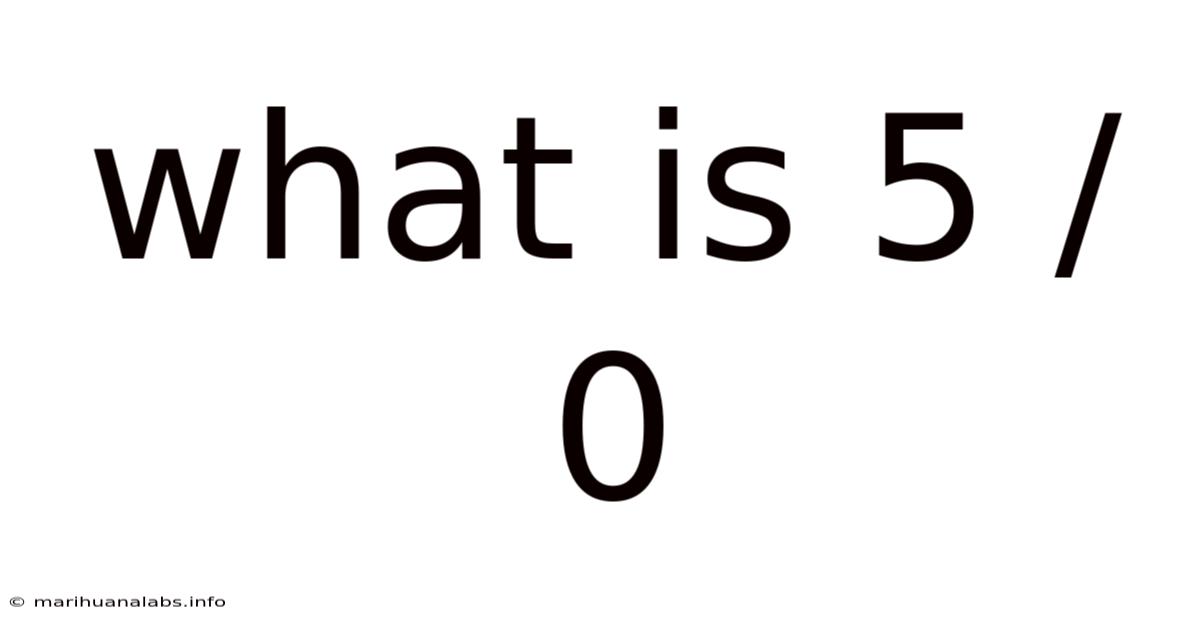
Table of Contents
What is 5 / 0? Understanding the Concept of Division by Zero
The question, "What is 5 / 0?" is a deceptively simple one that leads us down a fascinating path into the core principles of mathematics. At first glance, it might seem like a straightforward division problem. However, the answer isn't a simple number; instead, it delves into the fundamental rules of arithmetic and reveals the concept of undefined operations. This article will explore why division by zero is undefined, its implications in mathematics, and why it's crucial to understand this seemingly basic concept.
Introduction: The Intuition Behind Division
Before we tackle the enigma of division by zero, let's revisit the fundamental concept of division itself. Division is essentially the inverse operation of multiplication. When we say 5 / 1 = 5, we're asking, "What number, when multiplied by 1, equals 5?" The answer is clearly 5. Similarly, 10 / 2 = 5 because 5 multiplied by 2 equals 10. Division helps us determine how many times one number (the divisor) is contained within another number (the dividend).
This intuitive understanding works perfectly well when the divisor is a non-zero number. But what happens when we try to divide by zero? Let's try to apply the inverse multiplication approach. If we ask, "What number, when multiplied by zero, equals 5?", we immediately encounter a problem. Any number multiplied by zero will always result in zero, never 5. There is no number that satisfies this equation. This is the core reason why division by zero is undefined.
Why Division by Zero is Undefined: A Mathematical Explanation
The undefined nature of division by zero stems from several mathematical principles:
-
The multiplicative property of zero: Any number multiplied by zero equals zero. This is a fundamental axiom of arithmetic. This immediately eliminates the possibility of finding a solution to the equation x * 0 = 5, as there's no value of x that satisfies it.
-
Consistency in mathematical systems: Mathematics strives for consistency. Allowing division by zero would lead to contradictions and inconsistencies within the system. Consider this example:
If we were to assume that 5 / 0 = x for some number x, then we could multiply both sides by 0, resulting in 5 = x * 0. However, we know from the multiplicative property of zero that x * 0 = 0. This leads us to the contradictory statement 5 = 0, which is clearly false.
-
Limits and infinity: While division by zero is undefined, we can explore the behavior of the function f(x) = 5/x as x approaches zero. As x gets closer and closer to zero, the value of f(x) becomes arbitrarily large, approaching positive infinity if x approaches zero from the positive side and negative infinity if x approaches zero from the negative side. This concept is explored in calculus using limits, but it doesn't define 5/0 itself; it merely illustrates the behavior of the function near zero.
The Implications of Undefined Operations
The fact that division by zero is undefined has profound implications across various areas of mathematics and its applications:
-
Algebra: Solving algebraic equations requires careful attention to avoid division by zero. If an equation leads to a potential division by zero, it indicates that the solution may not exist or may be restricted to a specific domain.
-
Calculus: The concept of limits helps us to analyze functions as they approach points of discontinuity or singularity, such as division by zero. However, the limit itself does not define the value of the function at the point of singularity.
-
Computer programming: Most programming languages incorporate error handling to prevent division by zero, which often results in a runtime error or exception. Programmers must implement safeguards to avoid such errors.
-
Real-world applications: Division by zero can appear in real-world applications, such as those involving calculations with rates or proportions. Careful attention must be paid to ensure that the divisors are non-zero to prevent erroneous results.
Common Misconceptions about Division by Zero
Several misconceptions frequently arise regarding division by zero:
-
"5 / 0 = infinity": While the limit of 5/x as x approaches zero is infinity, this does not mean that 5/0 = infinity. Infinity is not a number in the conventional sense; it's a concept representing an unbounded quantity. Division by zero is not equal to any number, including infinity.
-
"5 / 0 = undefined is just a rule": The statement "division by zero is undefined" isn't simply an arbitrary rule; it's a direct consequence of the fundamental principles of arithmetic and the need for consistency within the mathematical system.
-
"My calculator says it's an error": Calculators are designed to prevent division by zero because the operation is mathematically undefined. The error message is not a limitation of the calculator but a reflection of the inherent mathematical impossibility.
Exploring Division by Zero Through Different Mathematical Lenses
Let's examine the concept from various mathematical perspectives to further solidify its undefined nature.
-
Set Theory: In set theory, division can be interpreted as partitioning a set into equal subsets. If we try to partition a set of 5 elements into 0 subsets, it's illogical and impossible. There's no way to divide a non-empty set into zero subsets.
-
Abstract Algebra: In abstract algebra, division is defined within the context of algebraic structures like groups and fields. In these structures, division by zero is often not even considered as a valid operation. The existence of multiplicative inverses, which is central to division, relies on non-zero divisors.
-
Complex Analysis: Even within the realm of complex numbers, where we extend the concept of numbers beyond the real line, division by zero remains undefined. The rules governing operations with complex numbers still uphold the principle of consistency and avoid contradictions arising from division by zero.
Practical Examples and Applications
Although division by zero is undefined, understanding its implications is vital in numerous real-world scenarios:
-
Physics: Formulas in physics often involve division. For instance, calculating velocity (speed) involves dividing distance by time. If the time is zero, the velocity is undefined. This doesn't necessarily mean the velocity is infinite; it simply means that the concept of velocity is not applicable in that scenario (instantaneous changes in position).
-
Engineering: Many engineering calculations use ratios and proportions. Dividing by zero in these calculations leads to undefined or erroneous results, leading to potential design flaws or safety risks.
-
Finance: Calculating rates of return or growth often involves dividing profits or gains by the investment amount. A zero investment amount makes the rate of return undefined.
Frequently Asked Questions (FAQ)
Q: What if I use a very small number instead of zero?
A: Using a very small number instead of zero will give you a large result. However, this does not define 5/0. It simply illustrates the behavior of 5/x as x approaches 0.
Q: Can division by zero ever be defined in some mathematical context?
A: No. Defining division by zero in standard arithmetic or its extensions would lead to inherent contradictions and break the fundamental rules of mathematics. While there might be specialized mathematical systems exploring extensions, they do not alter the fundamental undefined nature within the standard framework.
Q: Is there any practical use for understanding the concept of division by zero?
A: Absolutely. Understanding the concept of division by zero is crucial for preventing errors in calculations, avoiding paradoxes in mathematical reasoning, and writing robust computer programs that handle potential errors gracefully.
Conclusion: Embracing the Undefined
Division by zero is not merely an abstract mathematical concept; it's a foundational aspect of arithmetic that underlines the consistency and integrity of mathematical systems. Understanding why it's undefined is crucial for anyone who works with numbers, whether in a purely mathematical setting or in practical applications. It teaches us the importance of careful consideration of operations and the consequences of seemingly simple mistakes. Instead of searching for a numerical answer, embrace the fact that 5 / 0 is undefined, a cornerstone in our understanding of mathematics' fundamental rules. It highlights the necessity of a robust and logically consistent framework for mathematical reasoning and prevents the introduction of contradictions that would otherwise destabilize the entire system. Understanding this seemingly simple concept opens doors to a deeper appreciation of the elegance and rigor of mathematics.
Latest Posts
Latest Posts
-
How To Compute Flow Rate
Sep 19, 2025
-
Words That Rhyme With Understand
Sep 19, 2025
-
Passage From Book Crossword Clue
Sep 19, 2025
-
Book A Long Way Down
Sep 19, 2025
-
What Is Assurance And Audit
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 5 / 0 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.