What Is 45 Of 20
marihuanalabs
Sep 07, 2025 · 5 min read
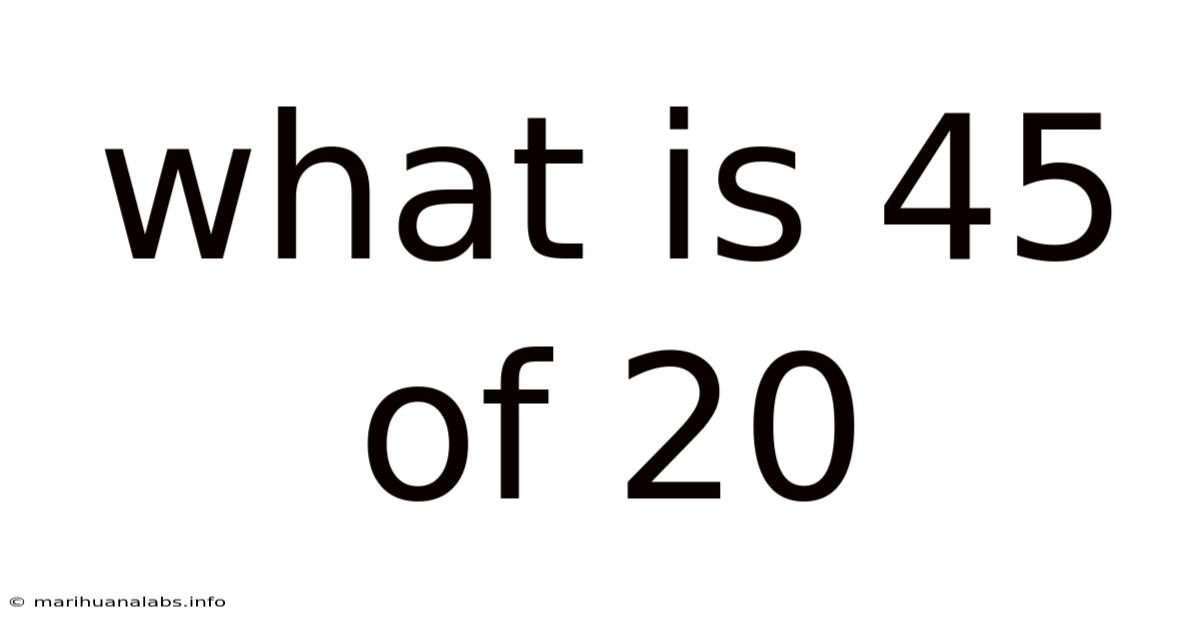
Table of Contents
What is 45% of 20? A Comprehensive Guide to Percentages
Finding a percentage of a number is a fundamental mathematical skill with widespread applications in everyday life, from calculating discounts and taxes to understanding statistics and financial data. This article will thoroughly explore how to calculate 45% of 20, providing various methods and explaining the underlying concepts. We'll move beyond a simple answer, delving into the principles of percentages, offering alternative calculation approaches, and addressing common misconceptions. By the end, you'll not only know the answer but also possess a deeper understanding of percentage calculations.
Understanding Percentages
A percentage is a fraction or ratio expressed as a number out of 100. The symbol "%" represents "per cent," meaning "out of one hundred." Therefore, 45% can be written as 45/100 or 0.45. Understanding this fundamental relationship is key to solving percentage problems.
Method 1: Using the Decimal Equivalent
This is arguably the most straightforward method. We convert the percentage into its decimal equivalent and then multiply it by the given number.
-
Convert the percentage to a decimal: To convert 45% to a decimal, we divide 45 by 100: 45 ÷ 100 = 0.45
-
Multiply by the given number: Now, we multiply the decimal equivalent (0.45) by the number we want to find the percentage of (20): 0.45 x 20 = 9
Therefore, 45% of 20 is $\boxed{9}$.
Method 2: Using Fractions
This method involves converting the percentage into a fraction and then performing the multiplication.
-
Convert the percentage to a fraction: 45% can be expressed as the fraction 45/100.
-
Simplify the fraction (optional): This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 5: (45 ÷ 5) / (100 ÷ 5) = 9/20
-
Multiply by the given number: Now, we multiply the simplified fraction (9/20) by 20: (9/20) x 20 = 9
Again, we arrive at the answer: 45% of 20 is $\boxed{9}$. This method showcases the elegant cancellation of the 20s, highlighting the interconnectedness of fractions and percentages.
Method 3: Using Proportions
This approach uses the concept of ratios and proportions to solve the problem. We set up a proportion where one ratio represents the percentage (45/100) and the other represents the unknown value (x/20).
-
Set up the proportion: 45/100 = x/20
-
Cross-multiply: To solve for x, we cross-multiply: 45 x 20 = 100x
-
Solve for x: This simplifies to 900 = 100x. Dividing both sides by 100 gives us x = 9
Hence, 45% of 20 is $\boxed{9}$. The proportion method provides a structured approach, particularly useful when dealing with more complex percentage problems.
Real-World Applications: Why This Matters
Understanding percentage calculations has numerous practical applications in various aspects of daily life:
-
Shopping: Calculating discounts, sales tax, and tips. If a $20 item is on sale for 45% off, you'd save $9 (45% of $20).
-
Finance: Determining interest rates, loan repayments, and investment returns. Understanding percentages is crucial for making informed financial decisions.
-
Science and Statistics: Representing data, analyzing trends, and interpreting research findings often involve percentages.
-
Everyday Life: Many everyday scenarios require percentage calculations, such as determining the percentage of a task completed or calculating the proportion of ingredients in a recipe.
Common Misconceptions about Percentages
Several common misunderstandings surrounding percentages can lead to errors in calculations. Let's address some of these:
-
Adding percentages directly: It's incorrect to assume that adding percentages directly yields the correct result. For example, a 10% increase followed by a 10% decrease does not result in the original value.
-
Misinterpreting percentage increase/decrease: A percentage increase or decrease is always relative to the initial value. A 50% increase on 10 is 15 (10 + 5), not 50 + 10 = 60.
-
Confusing percentage with absolute value: A percentage represents a proportion, not an absolute quantity. Saying "45% is 9" is incomplete without specifying "45% of 20 is 9".
Advanced Percentage Calculations: Building on the Fundamentals
The methods described above can be extended to solve more complex percentage problems. For instance:
-
Finding the original value: If you know the percentage and the resulting value, you can work backward to find the original value.
-
Calculating percentage change: This involves determining the percentage increase or decrease between two values.
-
Compound percentages: This involves calculating percentages successively, often used in finance to model interest accumulation.
Understanding these advanced concepts further builds your mathematical proficiency and problem-solving abilities.
Frequently Asked Questions (FAQ)
-
Q: Can I use a calculator to solve this? A: Absolutely! Calculators can significantly simplify percentage calculations, particularly for more complex problems. Simply enter 0.45 x 20.
-
Q: What if I need to find a different percentage of 20? A: You can apply the same methods (decimal, fraction, or proportion) by substituting the desired percentage for 45%.
-
Q: What are some real-world examples besides shopping and finance? A: Consider calculating the percentage of students who passed an exam, the percentage of land covered by forest, or the percentage of a population with a specific characteristic.
-
Q: Is there a quick mental math trick for this specific problem? A: For 45% of 20, you could think of it as half (50%) which is 10, and then subtract half of that (5%) which is 1. 10-1 = 9. This trick works best with easily divisible percentages.
Conclusion
Calculating 45% of 20 is a seemingly simple task, yet it serves as a gateway to understanding the broader concept of percentages. This article has provided multiple approaches, explained the underlying principles, and emphasized the importance of percentage calculations in diverse fields. Mastering these techniques empowers you to confidently tackle various percentage-related problems, enhancing your mathematical skills and improving your ability to navigate numerical information in everyday life. Remember to practice consistently, exploring different problems and methods to solidify your understanding. The more you practice, the easier and more intuitive percentage calculations will become.
Latest Posts
Latest Posts
-
Difference Between Greed And Gluttony
Sep 08, 2025
-
Name Of Group Of Horses
Sep 08, 2025
-
Its A Far Better Thing
Sep 08, 2025
-
Jack And The Beanstalk Book
Sep 08, 2025
-
The Pixies Que Sera Sera
Sep 08, 2025
Related Post
Thank you for visiting our website which covers about What Is 45 Of 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.