What Is 40 Of 90
marihuanalabs
Sep 18, 2025 · 5 min read
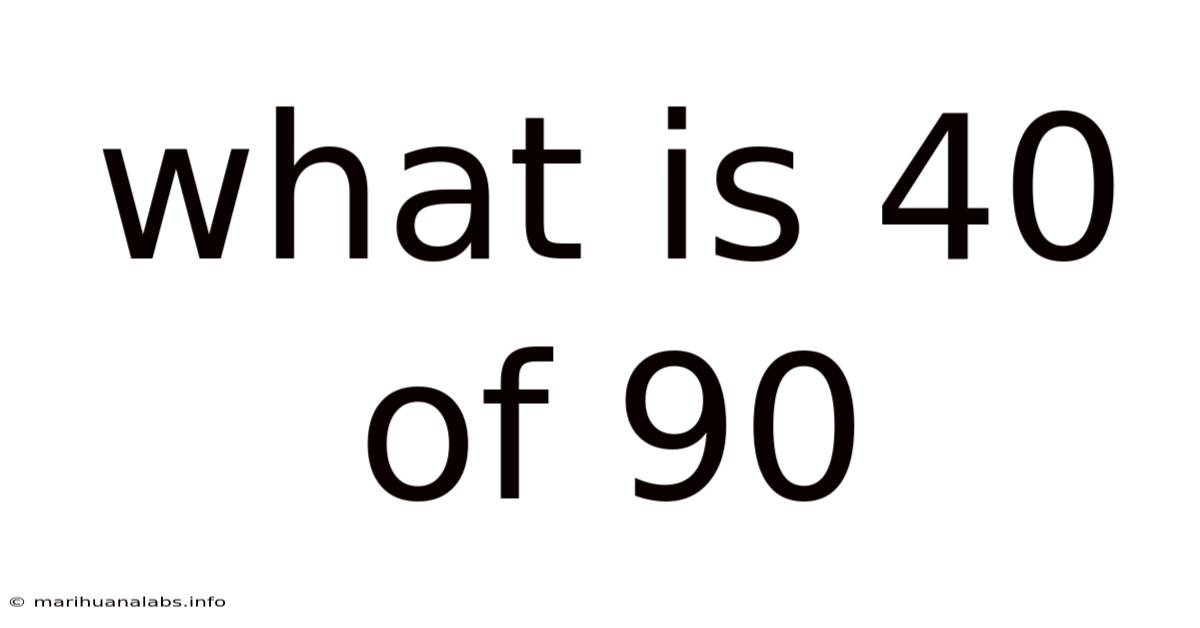
Table of Contents
What is 40% of 90? A Comprehensive Guide to Percentages and Their Applications
Finding a percentage of a number is a fundamental mathematical skill with widespread applications in everyday life, from calculating discounts and sales tax to understanding statistics and financial reports. This article will thoroughly explore the question "What is 40% of 90?" We'll delve into the calculation process, explain the underlying principles, and provide real-world examples to solidify your understanding of percentages. We'll also address frequently asked questions and explore advanced applications.
Understanding Percentages
Before we calculate 40% of 90, let's establish a firm understanding of what percentages represent. A percentage is simply a fraction expressed as a part of 100. The symbol "%" represents "per cent" or "out of 100." For example, 50% means 50 out of 100, which is equivalent to the fraction 50/100 or the decimal 0.5.
Calculating 40% of 90: The Step-by-Step Approach
There are several ways to calculate 40% of 90. Here are two common methods:
Method 1: Converting Percentage to Decimal
-
Convert the percentage to a decimal: To do this, divide the percentage by 100. So, 40% becomes 40/100 = 0.4.
-
Multiply the decimal by the number: Multiply the decimal (0.4) by the number you want to find the percentage of (90). 0.4 x 90 = 36.
Therefore, 40% of 90 is 36.
Method 2: Using Fractions
-
Convert the percentage to a fraction: 40% can be expressed as the fraction 40/100. This fraction can be simplified by dividing both the numerator and the denominator by their greatest common divisor, which is 20. This simplifies to 2/5.
-
Multiply the fraction by the number: Multiply the simplified fraction (2/5) by the number (90). (2/5) x 90 = 180/5 = 36.
Again, we find that 40% of 90 is 36.
Real-World Applications of Percentage Calculations
Understanding percentage calculations is essential for navigating various real-world scenarios. Here are a few examples:
-
Sales and Discounts: Imagine a store offering a 40% discount on an item priced at $90. Using our calculation, the discount would be $36, and the final price would be $90 - $36 = $54.
-
Taxes: If a sales tax is 40% and the pre-tax price of an item is $90, the tax amount would be $36, making the total cost $90 + $36 = $126.
-
Grade Calculations: Suppose a student scored 40 out of 90 points on a test. To calculate their percentage score, divide the score obtained by the total possible score and multiply by 100: (40/90) x 100 ≈ 44.44%.
-
Financial Analysis: Percentages are frequently used in financial statements to express ratios and proportions, such as profit margins, debt-to-equity ratios, and return on investment (ROI). Understanding these percentages is crucial for making informed financial decisions.
-
Statistical Analysis: Percentages are fundamental to presenting and interpreting statistical data. For instance, expressing survey results, polling data, or demographic information often involves the use of percentages.
Beyond the Basics: More Complex Percentage Problems
While calculating 40% of 90 is relatively straightforward, percentage problems can become more complex. Let's explore some variations:
-
Finding the Percentage: Suppose you bought an item for $36 and it represents 40% of the original price. To find the original price, you would divide the purchase price by the percentage (expressed as a decimal): $36 / 0.4 = $90.
-
Finding the Whole Number: If 36 represents 40% of a certain number, then you can set up an equation: 0.4x = 36, where x is the unknown number. Solving for x involves dividing both sides by 0.4: x = 36 / 0.4 = 90.
-
Calculating Percentage Increase or Decrease: Suppose a quantity increased from 90 to 126. To calculate the percentage increase, first find the difference (126 - 90 = 36). Then, divide the difference by the original quantity and multiply by 100: (36/90) x 100 = 40%. This indicates a 40% increase. Similarly, you can calculate percentage decreases.
-
Compound Percentages: These involve applying percentages successively. For instance, a 10% increase followed by a 20% increase is not equivalent to a 30% increase. Compound percentages require careful step-by-step calculations.
Frequently Asked Questions (FAQ)
Q: What are some common mistakes people make when calculating percentages?
A: Common errors include: forgetting to convert percentages to decimals, incorrectly multiplying or dividing, and misinterpreting the question, leading to incorrect calculations. Always double-check your work and ensure you understand what the question is asking.
Q: Are there any online tools or calculators that can help with percentage calculations?
A: Yes, numerous online percentage calculators are available. These tools can be helpful for quick calculations and verifying your own work. However, understanding the underlying principles is crucial for problem-solving and applying percentages in diverse contexts.
Q: How can I improve my understanding of percentages?
A: Practice is key. Start with simple problems and gradually increase the complexity. Try working through various real-world scenarios and use different methods to solve the same problem to strengthen your understanding. Consider using online resources, textbooks, or educational videos to supplement your learning.
Conclusion: Mastering Percentages for Everyday Success
Calculating 40% of 90, as we've shown, is a relatively simple calculation, yielding the answer 36. However, the underlying concept of percentages extends far beyond this specific example. A thorough grasp of percentage calculations is a vital skill applicable across various fields, from personal finance and shopping to scientific research and statistical analysis. By understanding the different methods of calculation, exploring real-world applications, and practicing regularly, you can build confidence and proficiency in this crucial mathematical skill. Remember that consistent practice and a clear understanding of the underlying concepts are the keys to mastering percentages and applying them successfully in your life.
Latest Posts
Latest Posts
-
Salts In The Periodic Table
Sep 18, 2025
-
7 9 As A Percentage
Sep 18, 2025
-
Street View Of New York
Sep 18, 2025
-
Composed Upon Westminster Bridge Poem
Sep 18, 2025
-
4 Types Of River Erosion
Sep 18, 2025
Related Post
Thank you for visiting our website which covers about What Is 40 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.