What Is 30 Of 75
marihuanalabs
Sep 12, 2025 · 5 min read
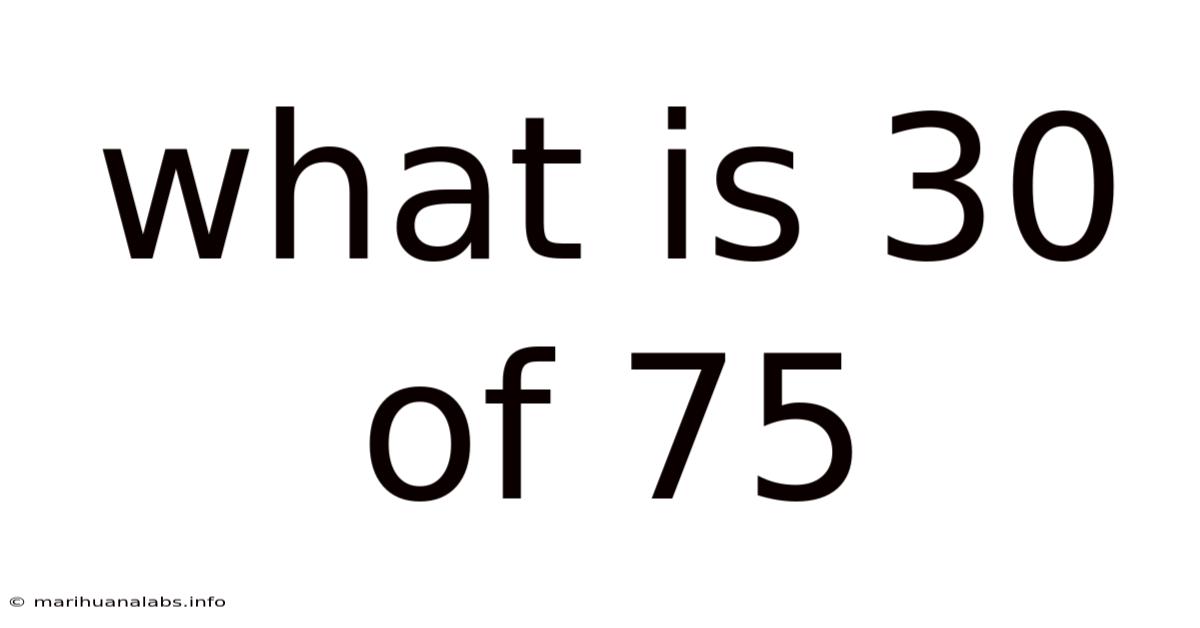
Table of Contents
What is 30 of 75? Unpacking Fractions, Percentages, and Ratios
Finding "30 of 75" might seem like a simple arithmetic problem, but it opens a door to understanding fundamental mathematical concepts like fractions, percentages, and ratios. This seemingly basic question provides a springboard for exploring these interconnected ideas and developing a deeper appreciation for their practical applications in everyday life. This article will not only answer the question directly but also delve into the underlying mathematical principles and provide multiple ways to solve similar problems.
Understanding the Question
The phrase "30 of 75" implies a relationship between two numbers: 30 and 75. We're essentially asking what portion, or fraction, 30 represents of the total 75. This relationship can be expressed in several ways, each offering a different perspective on the same underlying mathematical truth.
Method 1: Expressing it as a Fraction
The most straightforward approach is to represent the relationship as a fraction. A fraction shows a part (the numerator) in relation to a whole (the denominator). In this case:
- Numerator: 30 (the part)
- Denominator: 75 (the whole)
Therefore, "30 of 75" can be written as the fraction 30/75. This fraction is not in its simplest form, however. To simplify, we find the greatest common divisor (GCD) of 30 and 75, which is 15. Dividing both the numerator and denominator by 15, we get:
30/75 = (30 ÷ 15) / (75 ÷ 15) = 2/5
This simplified fraction, 2/5, tells us that 30 represents two-fifths of 75. This is a concise and accurate representation of the relationship.
Method 2: Calculating the Percentage
Percentages offer another way to express the relationship between 30 and 75. A percentage represents a fraction out of 100. To find the percentage, we first calculate the fraction (as shown above) and then convert it to a percentage by multiplying by 100:
(30/75) * 100 = 40%
This means that 30 is 40% of 75. Percentages are particularly useful for comparing proportions and expressing relative amounts, making them common in various contexts, from financial reports to scientific data analysis.
Method 3: Utilizing Ratios
Ratios provide a different perspective, focusing on the comparative relationship between two quantities. The ratio of 30 to 75 can be written as 30:75. Similar to the fraction, this ratio can be simplified by dividing both numbers by their GCD (15):
30:75 = 2:5
This simplified ratio, 2:5, indicates that for every 2 units of one quantity, there are 5 units of the other. Ratios are frequently used in scaling, comparing sizes, or describing mixtures. For example, a recipe might call for a 2:5 ratio of sugar to flour.
Applying the Concepts: Real-World Examples
These methods – fractions, percentages, and ratios – are not just abstract mathematical tools; they have practical applications in numerous real-life scenarios. Here are a few examples:
- Sales and Discounts: A store offers a discount of 30 dollars off a 75 dollar item. Understanding the percentage (40%) allows for easier calculation of discounts on other items.
- Surveys and Statistics: If 30 out of 75 respondents answered "yes" to a survey question, the percentage (40%) provides a clear summary of the responses.
- Cooking and Baking: A recipe might call for a certain ratio of ingredients. Understanding ratios allows for scaling recipes up or down.
- Financial Analysis: Financial statements often use ratios to analyze a company's performance (e.g., debt-to-equity ratio).
Expanding the Understanding: Further Mathematical Explorations
The simple question of "30 of 75" can lead to a deeper understanding of various mathematical concepts:
- Proportions: The relationship between 30 and 75 can be expressed as a proportion: 30/75 = x/100. Solving for x gives us the percentage (40%). Proportions are crucial in solving problems involving scaling and similar figures.
- Decimal Representation: The fraction 2/5 can also be expressed as a decimal: 0.4. Decimals provide another way to represent parts of a whole, frequently used in calculations and measurements.
- Algebraic Representation: The problem can be formulated algebraically: Let x represent the fraction; then x * 75 = 30. Solving for x gives x = 2/5 or 0.4 or 40%. This demonstrates how algebraic equations can be used to solve problems involving unknowns.
Frequently Asked Questions (FAQ)
Q1: What is the easiest way to solve "30 of 75"?
A1: The simplest approach is to express it as a fraction (30/75), simplify it (2/5), and then convert it to a percentage (40%) if needed.
Q2: Can I use a calculator to solve this?
A2: Yes, a calculator can be used to divide 30 by 75 and then multiply the result by 100 to find the percentage.
Q3: What if the numbers were larger or more complex?
A3: The same principles apply. Express the numbers as a fraction, simplify by finding the GCD, and then convert to a percentage or use a calculator for assistance.
Q4: Are there other ways to represent the relationship between 30 and 75?
A4: You could use a visual representation like a pie chart or bar graph to illustrate the proportion.
Conclusion
The seemingly simple question "What is 30 of 75?" provides a rich opportunity to explore fundamental mathematical concepts: fractions, percentages, and ratios. By understanding these concepts and their interrelationships, we gain valuable tools for solving various problems in everyday life and across different disciplines. This exploration shows how seemingly basic arithmetic can lead to a deeper understanding of mathematical principles and their practical relevance. The ability to express relationships between numbers in different forms – fractions, percentages, and ratios – enhances our ability to analyze data, interpret information, and solve problems more effectively. So next time you encounter a similar problem, remember the different approaches and their practical implications, transforming a simple arithmetic question into a gateway to broader mathematical understanding.
Latest Posts
Latest Posts
-
How To Measure Light Intensity
Sep 13, 2025
-
For Whom The Belle Tolls
Sep 13, 2025
-
Group Of Swans Are Called
Sep 13, 2025
-
Where Does Samba Come From
Sep 13, 2025
-
James Mcavoy As Mr Tumnus
Sep 13, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 75 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.