What Is 30 Of 2000
marihuanalabs
Sep 06, 2025 · 5 min read
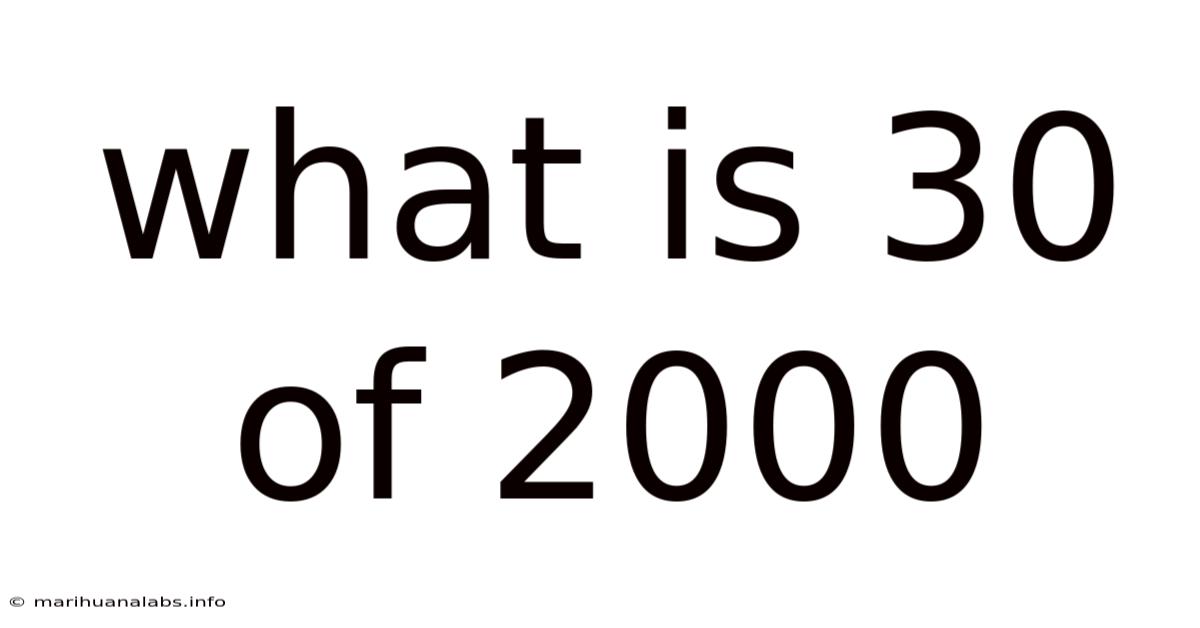
Table of Contents
What is 30/2000? Understanding Fractions, Percentages, and Decimals
Finding out "what is 30/2000?" might seem like a simple arithmetic problem, but it's a great jumping-off point to explore fundamental concepts in mathematics like fractions, percentages, and decimals. This article will not only solve the problem but also delve into the underlying principles, providing a comprehensive understanding for learners of all levels. We'll explore different methods for calculating the answer, discuss the practical applications of such calculations, and address frequently asked questions.
Introduction: Understanding Fractions
At its core, 30/2000 is a fraction. A fraction represents a part of a whole. The number on top (30) is called the numerator, indicating the number of parts we're considering. The number on the bottom (2000) is the denominator, indicating the total number of equal parts the whole is divided into. In this case, we're considering 30 parts out of a total of 2000 equal parts.
Calculating 30/2000: Step-by-Step Approach
There are several ways to solve this fraction:
Method 1: Simplification by Greatest Common Divisor (GCD)
The most efficient way to simplify a fraction is by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD is the largest number that divides both the numerator and denominator without leaving a remainder. In this case, the GCD of 30 and 2000 is 10.
We divide both the numerator and the denominator by 10:
30 ÷ 10 = 3 2000 ÷ 10 = 200
Therefore, 30/2000 simplifies to 3/200. This is the simplest form of the fraction, meaning it cannot be further simplified.
Method 2: Direct Conversion to Decimal
We can directly divide the numerator (30) by the denominator (2000) using a calculator or long division:
30 ÷ 2000 = 0.015
Therefore, 30/2000 is equal to 0.015 as a decimal.
Method 3: Conversion to Percentage
To express the fraction as a percentage, we first convert it to a decimal (as shown in Method 2) and then multiply by 100%:
0.015 x 100% = 1.5%
Therefore, 30/2000 represents 1.5%.
Understanding the Results: Different Representations of the Same Value
It's crucial to understand that 3/200, 0.015, and 1.5% all represent the same value – they are just different ways of expressing the same proportion. The choice of representation depends on the context and what is most easily understood or useful for the specific application. Fractions are useful for showing the precise relationship between parts and the whole. Decimals are commonly used in calculations and scientific applications. Percentages are especially helpful for comparing proportions and expressing relative amounts, making them widely used in everyday life, finance, and statistics.
Practical Applications of Fraction, Decimal, and Percentage Calculations
Understanding fractions, decimals, and percentages is crucial in numerous real-world scenarios:
-
Finance: Calculating interest rates, discounts, profit margins, and tax rates all rely on manipulating fractions, decimals, and percentages. For example, a 1.5% interest rate on a loan directly relates to our 30/2000 calculation.
-
Science: Many scientific calculations, particularly those involving ratios and proportions, utilize fractions and decimals. For instance, concentration of solutions in chemistry is often expressed as a percentage or a ratio.
-
Data Analysis: Representing data in the form of percentages or fractions is essential for making sense of statistical information and presenting findings clearly. For example, if 30 out of 2000 survey respondents answered a question in a particular way, that would be represented as 1.5%.
-
Everyday Life: Numerous everyday tasks involve proportions. For instance, calculating cooking ingredients based on a recipe, determining the amount of discount in a sale, or understanding the percentage of votes a candidate receives in an election all require working with fractions, decimals, and percentages.
Further Exploration: Working with More Complex Fractions
While 30/2000 is a relatively simple fraction, the principles discussed here apply to more complex fractions as well. The ability to simplify fractions, convert them to decimals and percentages, and understand their practical implications is a fundamental skill in mathematics. Practicing with more complex fractions will help build a solid foundation in mathematical reasoning. For example, try working through fractions like 125/5000 or 45/1500. You can use the same methods described above (finding the GCD, direct division, and multiplying by 100% for percentages) to solve these.
Frequently Asked Questions (FAQ)
Q1: Why is simplifying a fraction important?
A1: Simplifying fractions makes them easier to understand and work with. It gives you a clearer representation of the proportion and simplifies subsequent calculations.
Q2: Can I use a calculator for all these conversions?
A2: While a calculator can speed up the process, especially for larger numbers, understanding the underlying principles of fraction simplification and conversion is crucial for building a solid mathematical foundation.
Q3: What if the fraction is an improper fraction (where the numerator is larger than the denominator)?
A3: Improper fractions can be converted into mixed numbers (a whole number and a fraction) or directly divided to get a decimal. For instance, if you had a fraction like 2000/30, you would divide 2000 by 30 to obtain the decimal equivalent, which would be approximately 66.67.
Q4: Are there any online tools or resources that can help me practice with fractions, decimals, and percentages?
A4: Many educational websites and apps offer interactive exercises and tutorials to help you practice these concepts. These resources often provide immediate feedback and explanations, making learning more efficient and enjoyable.
Conclusion: Mastering the Fundamentals
Understanding "what is 30/2000?" extends far beyond a simple arithmetic problem. It's about grasping the fundamental concepts of fractions, decimals, and percentages, and how they are interconnected. These concepts are not just abstract mathematical ideas; they are essential tools used in countless aspects of everyday life, professional fields, and advanced studies. By mastering these fundamental skills, you'll build a strong foundation for more complex mathematical concepts and equip yourself with valuable skills applicable across various disciplines. Remember, consistent practice and a curious approach to learning are key to mastering these concepts and unlocking their full potential.
Latest Posts
Latest Posts
-
Graph Price Elasticity Of Demand
Sep 07, 2025
-
In The Night Kitchen Sendak
Sep 07, 2025
-
Conjugation Of The Verb Gustar
Sep 07, 2025
-
What Is Ummah In Islam
Sep 07, 2025
-
1 93 M In Feet
Sep 07, 2025
Related Post
Thank you for visiting our website which covers about What Is 30 Of 2000 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.