What Is 20 Of 65
marihuanalabs
Sep 16, 2025 · 5 min read
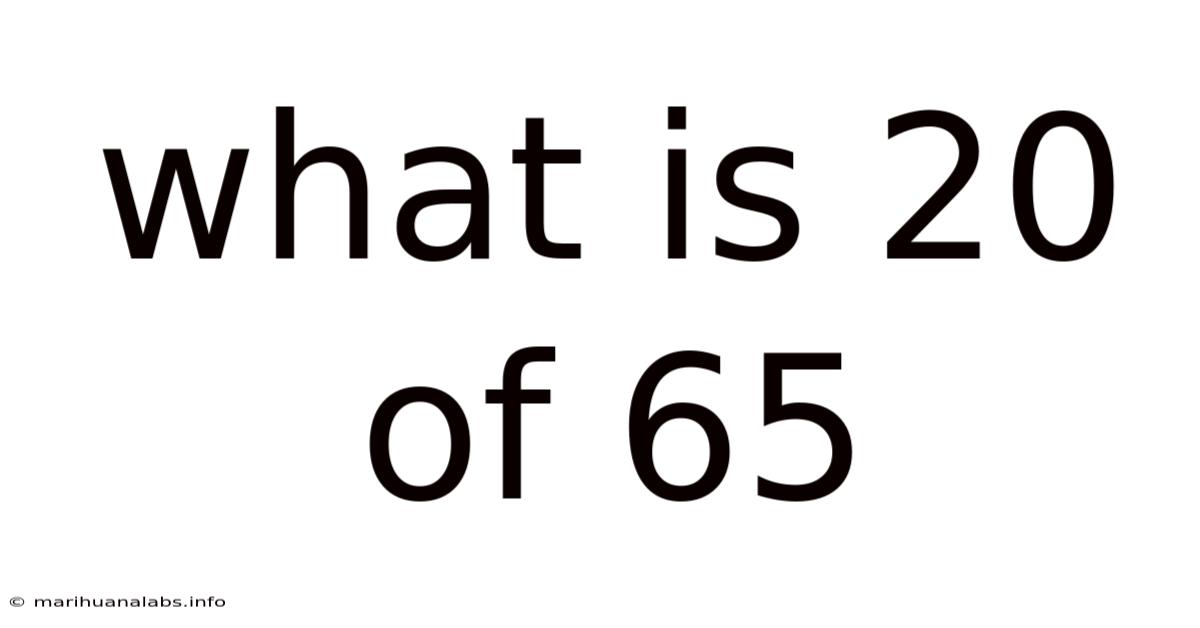
Table of Contents
What is 20 of 65? Understanding Fractions, Percentages, and Ratios
This article explores the question "What is 20 of 65?" in a comprehensive manner, going beyond a simple numerical answer to delve into the underlying mathematical concepts and their real-world applications. We'll unpack how to calculate this, explaining fractions, percentages, and ratios – providing you with a solid understanding of how to tackle similar problems in the future.
Introduction: More Than Just a Number
The seemingly simple question, "What is 20 of 65?", actually touches upon fundamental mathematical concepts. It's not just about finding a numerical solution; it's about understanding the relationship between 20 and 65. This relationship can be expressed in several ways, primarily as a fraction, a percentage, or a ratio. Understanding these representations is crucial for various applications across different fields, from finance and statistics to everyday life scenarios.
1. Understanding Fractions: Representing Parts of a Whole
A fraction represents a part of a whole. It's written as a/b, where 'a' is the numerator (the part) and 'b' is the denominator (the whole). In our case, "20 of 65" can be expressed as the fraction 20/65. This fraction represents 20 parts out of a total of 65 parts.
-
Simplifying Fractions: To make fractions easier to understand and compare, we often simplify them by finding the greatest common divisor (GCD) of the numerator and denominator. The GCD of 20 and 65 is 5. Dividing both the numerator and the denominator by 5, we get:
20/65 = (20 ÷ 5) / (65 ÷ 5) = 4/13
This simplified fraction, 4/13, represents the same proportion as 20/65 but is more concise. It means that 20 out of 65 is equivalent to 4 out of 13.
2. Converting Fractions to Percentages: Expressing Proportion in Hundredths
Percentages provide a standardized way to express proportions. A percentage is a fraction where the denominator is always 100. To convert the fraction 4/13 to a percentage, we perform the following calculation:
(4/13) * 100% ≈ 30.77%
Therefore, 20 out of 65 represents approximately 30.77%. This means that 20 is roughly 30.77% of 65.
3. Understanding Ratios: Comparing Two Quantities
A ratio compares two or more quantities. The ratio of 20 to 65 can be written as 20:65 or 20/65. Similar to fractions, ratios can be simplified by finding the GCD. In this case, the simplified ratio is 4:13. This indicates that for every 4 units of one quantity, there are 13 units of the other quantity.
4. Real-World Applications: Where This Knowledge Matters
Understanding fractions, percentages, and ratios is crucial in many real-world situations:
-
Finance: Calculating interest rates, discounts, profit margins, and investment returns all rely on these concepts. For example, if a store offers a 30% discount on a $65 item, the discount amount is calculated as 30.77% of $65, which is approximately $20.
-
Statistics: Analyzing data, such as survey results or population demographics, often involves working with fractions, percentages, and ratios.
-
Science: Many scientific concepts, including chemical proportions and probabilities, are expressed using fractions and ratios. For example, a chemist might work with a solution containing a 4:13 ratio of solute to solvent.
-
Everyday Life: Cooking recipes, measuring ingredients, and dividing tasks all involve using proportions and fractions.
5. Beyond the Basics: Further Exploration of Proportions
The concepts of fractions, percentages, and ratios are intertwined. Understanding their interrelationships allows for flexible problem-solving. For example, you can easily convert between these representations:
- Fraction to Percentage: Multiply the fraction by 100%.
- Percentage to Fraction: Divide the percentage by 100 and simplify the resulting fraction.
- Ratio to Fraction: A ratio a:b can be written as the fraction a/b.
- Fraction to Ratio: A fraction a/b can be expressed as the ratio a:b.
6. Solving Similar Problems: A Step-by-Step Guide
Let's consider another example: What is 15 of 75?
- Express as a fraction: 15/75
- Simplify the fraction: Find the GCD (15). 15/75 = (15÷15)/(75÷15) = 1/5
- Convert to a percentage: (1/5) * 100% = 20%
- Express as a ratio: 1:5
Therefore, 15 of 75 is 1/5, or 20%, or 1:5.
7. Addressing Common Misconceptions:
- Order of operations: Remember that the order of operations (PEMDAS/BODMAS) matters in more complex calculations involving fractions and percentages.
- Rounding: When converting fractions to percentages, rounding may be necessary. Always specify the level of precision required.
- Units: When dealing with real-world problems, ensure you are consistent with your units (e.g., dollars, meters, kilograms).
8. Frequently Asked Questions (FAQ):
-
Q: What's the difference between a fraction and a ratio?
- A: While they are closely related and can be used interchangeably in many contexts, a fraction represents a part of a whole, whereas a ratio compares two or more quantities.
-
Q: How do I choose between using a fraction, percentage, or ratio?
- A: The best choice depends on the context. Percentages are often preferred for comparisons, while fractions are useful for precise calculations. Ratios are helpful when comparing quantities.
-
Q: What if I have a decimal instead of a whole number?
- A: The principles remain the same. You can work with decimals in fractions and percentages. For example, 2.5 out of 10 can be represented as the fraction 2.5/10, which simplifies to 1/4 or 25%.
-
Q: Can I use a calculator for these calculations?
- A: Absolutely! Calculators can simplify fractions and convert between fractions, percentages, and decimals, saving you time and effort on complex calculations.
9. Conclusion: Mastering Proportions
Understanding "what is 20 of 65" goes far beyond simply obtaining the answer of approximately 30.77%. It's about grasping the core mathematical concepts of fractions, percentages, and ratios and recognizing their broad applications. By mastering these concepts, you equip yourself with a valuable skillset applicable across various fields and daily life situations. The ability to interpret and manipulate proportions empowers you to make informed decisions, solve problems efficiently, and understand the world around you more effectively. Remember to practice regularly to solidify your understanding and build confidence in your mathematical abilities. The more you work with these concepts, the easier they will become, and the more you'll appreciate their power and versatility.
Latest Posts
Latest Posts
-
Holding The Line Barbara Kingsolver
Sep 16, 2025
-
Semi Variable Cost With Example
Sep 16, 2025
-
Instruments That Start With M
Sep 16, 2025
-
What Is German For England
Sep 16, 2025
-
I Like To In French
Sep 16, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 65 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.