What Is 20 Of 45
marihuanalabs
Sep 15, 2025 · 5 min read
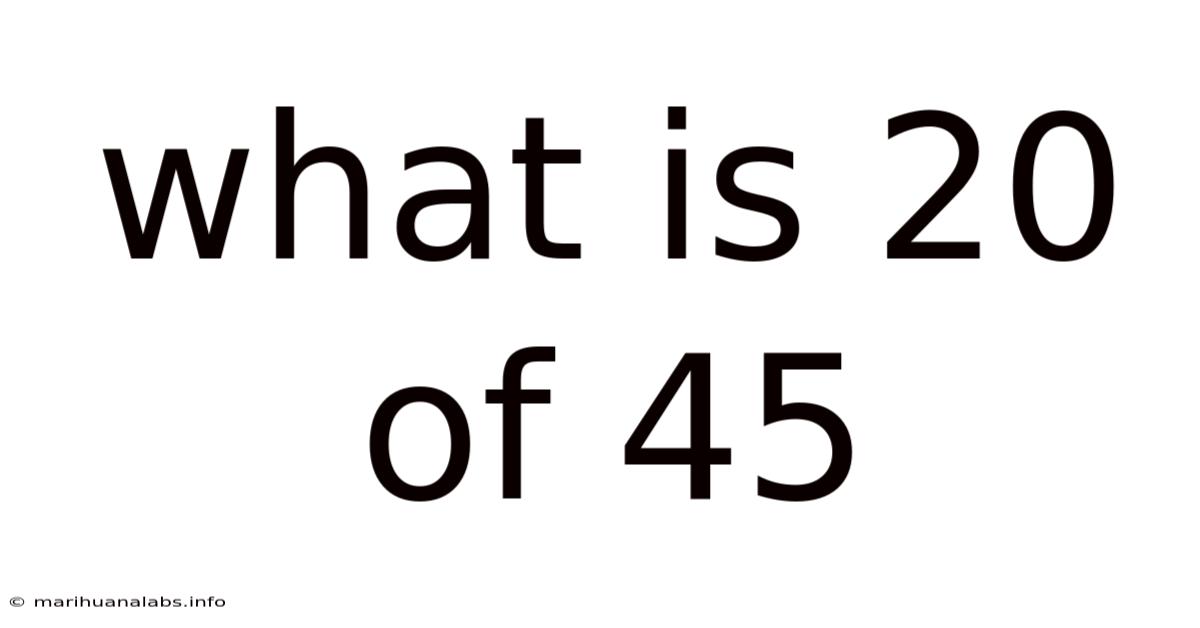
Table of Contents
What is 20 of 45? Unveiling the World of Fractions, Percentages, and Ratios
Finding "20 of 45" might seem like a simple arithmetic problem, but it opens the door to understanding fundamental mathematical concepts like fractions, percentages, and ratios. This seemingly straightforward question allows us to explore different ways to represent the relationship between two numbers, highlighting their practical applications in everyday life. This comprehensive guide will not only answer "what is 20 of 45?" but will also delve into the underlying mathematical principles, providing you with a solid foundation in these essential concepts.
Understanding the Problem: Fractions, Percentages, and Ratios
The phrase "20 of 45" implies a part-to-whole relationship. We have a part (20) and a whole (45). There are several ways to express this relationship mathematically:
-
Fraction: The most direct way to represent this relationship is as a fraction: 20/45. This signifies 20 out of 45.
-
Percentage: A percentage expresses the fraction as a proportion of 100. To find the percentage, we calculate (20/45) * 100%.
-
Ratio: A ratio compares two quantities. In this case, the ratio is 20:45, which can be simplified.
Calculating the Fraction: Simplifying 20/45
The fraction 20/45 isn't in its simplest form. To simplify a fraction, we find the greatest common divisor (GCD) of the numerator (20) and the denominator (45) and divide both by it.
The factors of 20 are 1, 2, 4, 5, 10, and 20. The factors of 45 are 1, 3, 5, 9, 15, and 45.
The greatest common divisor of 20 and 45 is 5.
Therefore, we divide both the numerator and denominator by 5:
20 ÷ 5 = 4 45 ÷ 5 = 9
The simplified fraction is 4/9. This means that 20 out of 45 is equivalent to 4 out of 9.
Converting the Fraction to a Percentage
To express 20/45 (or its simplified form, 4/9) as a percentage, we multiply the fraction by 100%:
(4/9) * 100% ≈ 44.44%
Therefore, 20 out of 45 is approximately 44.44%. The percentage shows the proportional part 20 represents within the whole 45.
Understanding Ratios and Proportions
The ratio of 20 to 45 is expressed as 20:45. Like the fraction, this ratio can be simplified by dividing both numbers by their GCD (5):
20 ÷ 5 = 4 45 ÷ 5 = 9
The simplified ratio is 4:9. This indicates that for every 4 parts of one quantity, there are 9 parts of another. Ratios are crucial in comparing different quantities and establishing proportions.
Real-World Applications: Illustrative Examples
Understanding fractions, percentages, and ratios is vital in numerous real-world scenarios:
-
Cooking: A recipe calls for 20 grams of sugar in a total mixture of 45 grams. The fraction 20/45 (or 4/9) represents the proportion of sugar in the recipe.
-
Sales and Discounts: A store offers a discount of 20 dollars on an item originally priced at 45 dollars. The percentage discount is approximately 44.44%.
-
Test Scores: A student answered 20 questions correctly out of a total of 45 questions. Their score is represented by the fraction 20/45 (or 4/9), and their percentage score is approximately 44.44%.
-
Statistics and Probability: In a sample of 45 people, 20 prefer a certain brand. The fraction 20/45 (or 4/9) represents the proportion of people who prefer that brand.
-
Data Analysis: Many data analysis tasks involve comparing proportions or parts of a whole, making fractions and percentages essential tools. For example, analyzing survey results or sales figures often relies on these calculations.
Expanding the Understanding: Further Exploration
This problem opens doors to exploring more complex concepts:
-
Decimal Representation: The fraction 4/9 can also be expressed as a decimal: 0.444... (a repeating decimal). This shows another way of representing the proportion.
-
Proportionality: Understanding the concept of proportionality is essential in solving problems where the relationship between two quantities remains constant even when their values change. For instance, if we increase the whole (45) proportionally, the part (20) will also increase proportionally, maintaining the same ratio (4:9).
-
Algebraic Representation: The problem can be expressed algebraically. Let x represent the whole and y represent the part. We can write the relationship as y/x = 20/45, which simplifies to y/x = 4/9. This algebraic representation is useful for solving more complex problems where variables are unknown.
Frequently Asked Questions (FAQs)
Q1: Can I use a calculator to solve this?
A1: Absolutely! A calculator can quickly convert fractions to decimals and percentages. However, understanding the underlying principles of simplification and conversion is crucial for applying these concepts in different contexts.
Q2: What if the numbers were larger?
A2: The process remains the same. You would find the GCD of the numerator and denominator to simplify the fraction and then convert it to a percentage or express it as a ratio. For very large numbers, a calculator becomes more practical.
Q3: Are fractions, percentages, and ratios interchangeable?
A3: While they represent the same relationship, they provide different ways to express that relationship. The choice of which one to use often depends on the context and the information needed. Percentages are commonly used for comparisons and to show proportions relative to 100, while ratios focus on the relationship between two numbers. Fractions provide a more precise representation.
Conclusion: Beyond the Numbers
The simple question "What is 20 of 45?" serves as a gateway to a deeper understanding of crucial mathematical concepts. Mastering fractions, percentages, and ratios is not just about performing calculations; it's about developing a strong numerical sense and applying these skills to diverse real-world situations. By understanding these foundational concepts, you equip yourself with powerful tools for problem-solving, data interpretation, and decision-making across various fields. From cooking to finance, from science to everyday life, the ability to manipulate and interpret these mathematical expressions is a valuable asset. This article hopefully not only provided a clear answer but also sparked a greater appreciation for the significance of these fundamental mathematical relationships.
Latest Posts
Latest Posts
-
A Conversation With Oscar Wilde
Sep 15, 2025
-
Point Of Care Testing Devices
Sep 15, 2025
-
Difference Between Burglary And Theft
Sep 15, 2025
-
Themes In Death Of Salesman
Sep 15, 2025
-
What Is The Standard Solution
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.