What Is 20 Of 350
marihuanalabs
Sep 23, 2025 · 5 min read
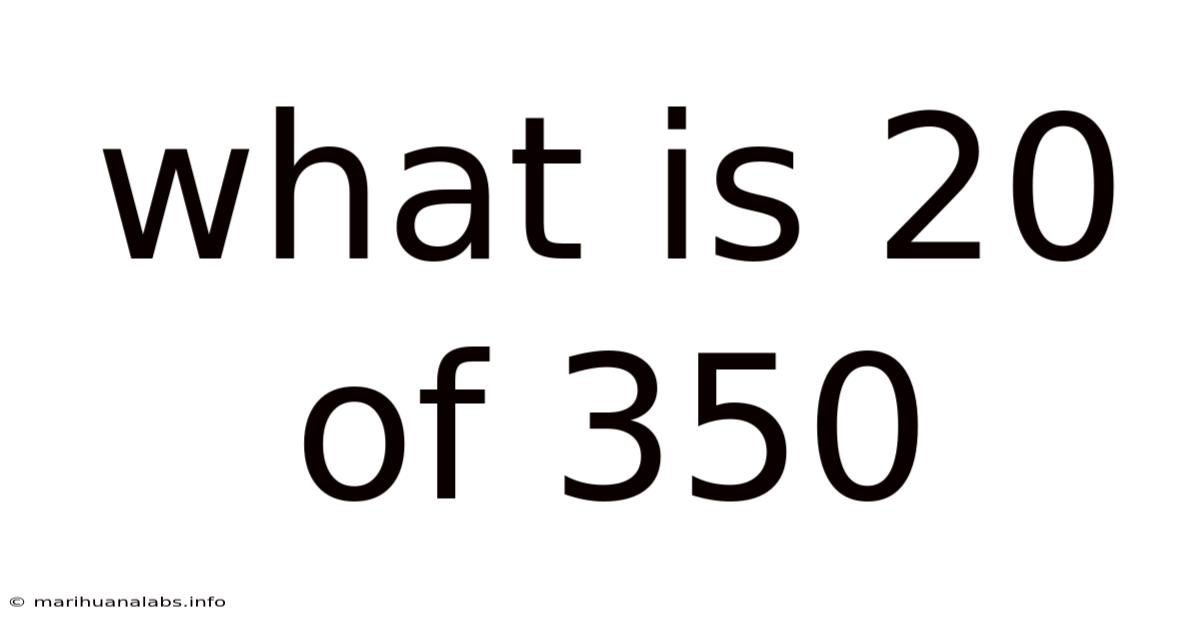
Table of Contents
What is 20 of 350? Understanding Percentages and Fractions
This article explores the question "What is 20 of 350?" It goes beyond simply providing the answer, delving into the fundamental concepts of fractions, percentages, and ratios, explaining how to calculate such values and offering practical applications. We'll also examine different methods for solving this type of problem and address common misconceptions. Understanding these concepts is crucial in various fields, from everyday budgeting to advanced scientific calculations. This comprehensive guide aims to empower you with the skills to confidently tackle similar problems independently.
Understanding the Problem: 20 out of 350
The question "What is 20 of 350?" essentially asks us to determine the proportion that 20 represents within the larger number 350. This can be expressed in several ways:
- As a fraction: 20/350
- As a percentage: What percentage of 350 is 20?
- As a ratio: The ratio of 20 to 350
Method 1: Calculating the Fraction and Simplifying
The most straightforward approach is to express the relationship as a fraction: 20/350. This fraction represents the part (20) over the whole (350). To understand this proportion better, we need to simplify the fraction to its lowest terms. This involves finding the greatest common divisor (GCD) of both the numerator (20) and the denominator (350).
The GCD of 20 and 350 is 10. Dividing both the numerator and the denominator by 10, we get:
20 ÷ 10 = 2 350 ÷ 10 = 35
Therefore, the simplified fraction is 2/35. This means that 20 represents 2 out of every 35 parts of 350.
Method 2: Converting the Fraction to a Percentage
To express the proportion as a percentage, we convert the fraction 20/350 (or its simplified form 2/35) into a decimal and then multiply by 100.
First, let's divide 20 by 350:
20 ÷ 350 ≈ 0.05714
Now, multiply the decimal by 100 to express it as a percentage:
0.05714 × 100 ≈ 5.71%
Therefore, 20 is approximately 5.71% of 350.
Method 3: Using Proportions
Another approach is to set up a proportion. We can express the problem as:
20/350 = x/100
Where 'x' represents the percentage we're trying to find. To solve for 'x', we cross-multiply:
20 × 100 = 350 × x 2000 = 350x
Now, divide both sides by 350:
x = 2000 ÷ 350 ≈ 5.71
Therefore, x ≈ 5.71%, confirming our previous result.
Understanding Ratios
The relationship between 20 and 350 can also be expressed as a ratio: 20:350. Like fractions, ratios represent the comparative sizes of two or more quantities. This ratio can be simplified by dividing both numbers by their GCD (10), resulting in the simplified ratio of 2:35. This indicates that for every 2 parts, there are 35 parts in the total of 350.
Practical Applications
Understanding how to calculate proportions, percentages, and ratios is vital in many real-world scenarios:
- Finance: Calculating interest rates, discounts, profit margins, and investment returns all involve working with percentages and proportions.
- Statistics: Analyzing data, understanding probabilities, and interpreting survey results require proficiency in these concepts.
- Science: Many scientific calculations involve expressing relationships between quantities as fractions, percentages, or ratios. For example, determining the concentration of a solution or the percentage composition of a compound.
- Everyday Life: Estimating tips, calculating sale prices, and understanding proportions in recipes are common applications.
Further Exploration: Working with Larger Numbers and Decimals
The methods described above apply equally well to larger numbers and decimal values. The core concepts remain the same: expressing the relationship as a fraction, simplifying, converting to a percentage, or working with proportions. For larger numbers, using a calculator is highly recommended to ensure accuracy.
For example, let's consider the problem: "What is 125 of 2500?"
- Fraction: 125/2500
- Simplification: The GCD of 125 and 2500 is 125. Dividing both by 125, we get 1/20.
- Percentage: 1/20 = 0.05. Multiplying by 100 gives 5%.
- Ratio: 125:2500 simplifies to 1:20.
Common Misconceptions
- Confusing numerator and denominator: It's crucial to remember that the numerator represents the part and the denominator represents the whole.
- Incorrect simplification of fractions: Ensure you are dividing both the numerator and denominator by their GCD to obtain the simplest form.
- Rounding errors: When converting to percentages, rounding off too early can lead to inaccuracies in the final result. It's best to carry out calculations to several decimal places before rounding.
Frequently Asked Questions (FAQ)
Q: Can I use a calculator to solve these problems?
A: Yes, absolutely! Calculators are particularly helpful when dealing with larger numbers or decimal values.
Q: What if the numbers aren't whole numbers?
A: The same principles apply. You'll still express the relationship as a fraction, simplify if possible, and convert to a percentage as needed.
Q: Why is it important to simplify fractions?
A: Simplifying fractions makes the proportion easier to understand and interpret. It provides a clearer representation of the relationship between the two quantities.
Q: Are percentages always expressed to two decimal places?
A: While two decimal places are common, the number of decimal places used depends on the context and the required level of accuracy.
Conclusion: Mastering Proportions, Percentages, and Ratios
The question "What is 20 of 350?" provides a springboard for understanding the fundamental concepts of fractions, percentages, and ratios. Mastering these concepts is not just about performing calculations; it's about developing a deeper understanding of proportional relationships that underpin many aspects of mathematics and its applications in the real world. By practicing different methods and addressing common misconceptions, you'll gain the confidence to tackle similar problems and apply these skills effectively in various contexts. Remember that the key is to understand the underlying principles and choose the most appropriate method for each specific problem. With practice and consistent application, you’ll become proficient in working with proportions, percentages, and ratios, unlocking their power to solve a wide range of problems.
Latest Posts
Latest Posts
-
Of Mice And Men Candy
Sep 23, 2025
-
Chaucer Book Of The Duchess
Sep 23, 2025
-
How To Know My Genotype
Sep 23, 2025
-
Graph Of X 3 1
Sep 23, 2025
-
Regions Of The Uk Map
Sep 23, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 350 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.