What Is 20 Of 24
marihuanalabs
Sep 08, 2025 · 5 min read
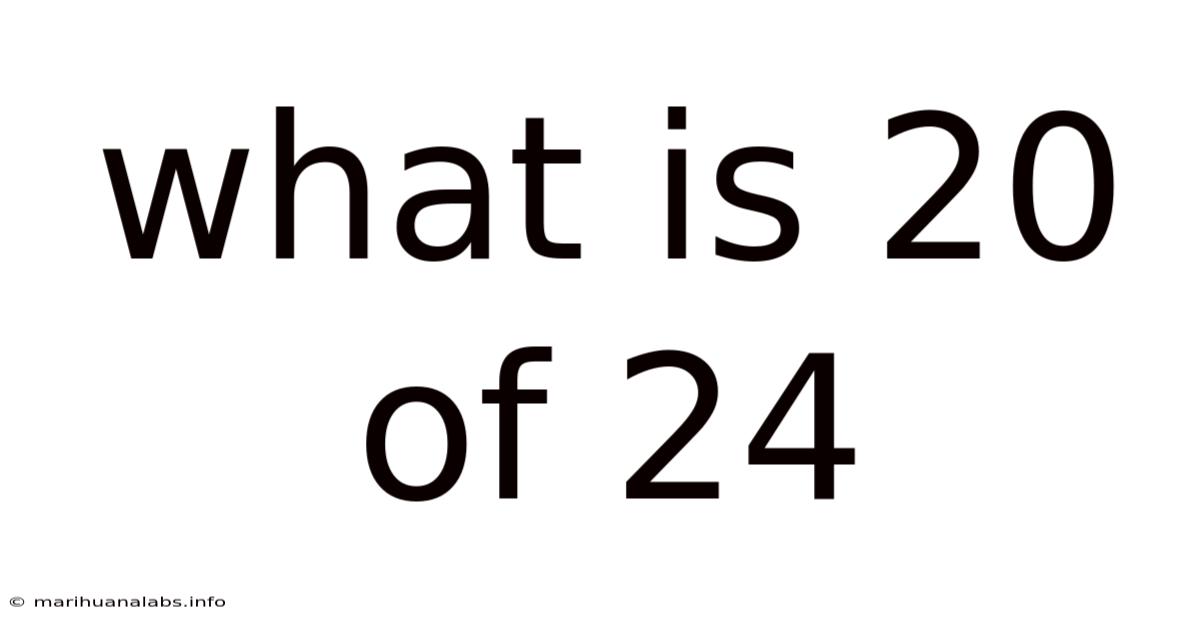
Table of Contents
What is 20 of 24? Understanding Fractions, Ratios, and Percentages
What is 20 of 24? This seemingly simple question opens a door to a fascinating world of mathematical concepts, including fractions, ratios, and percentages. Understanding how to solve this, and similar problems, is crucial for everyday life, from calculating discounts to understanding statistics. This article will guide you through several ways to approach this problem, offering a comprehensive explanation suitable for learners of all levels. We'll delve into the core concepts, explore different methods of calculation, and even look at real-world applications.
Understanding the Question
The phrase "20 of 24" implies a part-to-whole relationship. We have a whole quantity of 24, and we're interested in a specific part of that whole, which is 20. This relationship can be expressed in several ways: as a fraction, a ratio, or a percentage. Let's explore each representation.
1. Representing "20 of 24" as a Fraction
A fraction expresses a part of a whole. In this case, the part is 20, and the whole is 24. Therefore, the fraction representing "20 of 24" is 20/24.
This fraction can be simplified by finding the greatest common divisor (GCD) of 20 and 24. The GCD of 20 and 24 is 4. Dividing both the numerator (20) and the denominator (24) by 4 gives us the simplified fraction 5/6.
This simplified fraction, 5/6, represents the same proportion as 20/24; it's just a more concise way of expressing it. It means that 20 out of 24 is equivalent to 5 out of 6.
2. Representing "20 of 24" as a Ratio
A ratio compares two quantities. We can express "20 of 24" as a ratio of 20:24. Similar to fractions, this ratio can be simplified by dividing both numbers by their GCD (4), resulting in the simplified ratio of 5:6. This ratio means that for every 5 parts, there are a total of 6 parts.
3. Representing "20 of 24" as a Percentage
A percentage represents a fraction out of 100. To convert the fraction 20/24 (or its simplified form 5/6) into a percentage, we perform the following calculation:
(20/24) * 100% = 83.333...%
Rounding to two decimal places, we get 83.33%. This means that 20 out of 24 represents approximately 83.33% of the whole.
Different Approaches to Solving the Problem
Let's explore different methods to arrive at the same answers.
-
Direct Calculation: The most straightforward approach is to directly calculate the fraction 20/24 and then convert it to a percentage. This involves dividing 20 by 24 and multiplying the result by 100.
-
Simplification First: Simplifying the fraction before converting to a percentage often makes the calculation easier. Simplifying 20/24 to 5/6 before calculating the percentage involves dividing 5 by 6 and multiplying by 100, which is simpler than working with larger numbers.
-
Using Proportions: We can set up a proportion to solve for the percentage. Let x represent the percentage:
20/24 = x/100
Cross-multiplying gives:
24x = 2000
Solving for x:
x = 2000/24 = 83.33%
This method provides a clear and structured way to calculate the percentage.
The Importance of Understanding Fractions, Ratios, and Percentages
These concepts are fundamental to various aspects of daily life and many academic disciplines. Here are a few examples:
-
Shopping: Calculating discounts, sales tax, and comparing prices often involves using percentages and fractions. For example, a 25% discount means you pay 75% of the original price (100% - 25% = 75%).
-
Cooking and Baking: Recipes often use ratios and fractions to specify ingredient amounts. Understanding these concepts is essential for accurate measurements and successful results.
-
Finance: Understanding percentages is crucial for managing personal finances, calculating interest rates, and analyzing investments.
-
Data Analysis: Percentages and ratios are frequently used to represent data and statistics in a clear and concise manner. This is important for interpreting charts, graphs, and reports.
-
Science: In scientific research, fractions, ratios, and percentages are used extensively in measurements, calculations, and data representation.
Frequently Asked Questions (FAQ)
-
Q: What if the numbers were different? How would I solve "15 of 25"?
-
A: The same principles apply. You would express this as the fraction 15/25, simplify it (to 3/5), and then convert it to a percentage (60%).
-
Q: Can I use a calculator to solve these problems?
-
A: Yes, absolutely! Calculators are useful tools for performing these calculations quickly and accurately. However, understanding the underlying concepts is essential for solving problems effectively, even without a calculator.
-
Q: Why is simplifying fractions important?
-
A: Simplifying fractions makes the calculations easier and often allows for a better understanding of the relationship between the two numbers. It helps to see the core relationship between the parts and the whole.
-
Q: What if the "part" is larger than the "whole"?
-
A: This scenario would result in a fraction, ratio, or percentage greater than 1 (or 100%). This can occur in situations where you are dealing with quantities that increase over time or have multiple parts. It simply means that the "part" exceeds the initial "whole."
Conclusion:
The answer to "What is 20 of 24?" is multifaceted. It can be expressed as the fraction 20/24 (simplified to 5/6), the ratio 20:24 (simplified to 5:6), or the percentage 83.33%. Understanding the methods used to arrive at these answers is far more important than simply knowing the numerical result. The ability to work with fractions, ratios, and percentages is a crucial skill with far-reaching applications in numerous areas of life. Mastering these mathematical concepts not only helps in solving everyday problems but also builds a strong foundation for more advanced mathematical studies. By understanding the core principles and applying them to different situations, you'll develop a robust mathematical skill set that will serve you well throughout your life. So, the next time you encounter a similar problem, remember the principles outlined here, and you'll be well-equipped to tackle it with confidence.
Latest Posts
Latest Posts
-
35 Degree Fahrenheit To Celsius
Sep 09, 2025
-
Is Saturn Hot Or Cold
Sep 09, 2025
-
Twelve Angry Men Juror 8
Sep 09, 2025
-
Could I Have In Spanish
Sep 09, 2025
-
Whats 28 Days From Today
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 24 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.