What Is 20 Of 14
marihuanalabs
Sep 09, 2025 · 6 min read
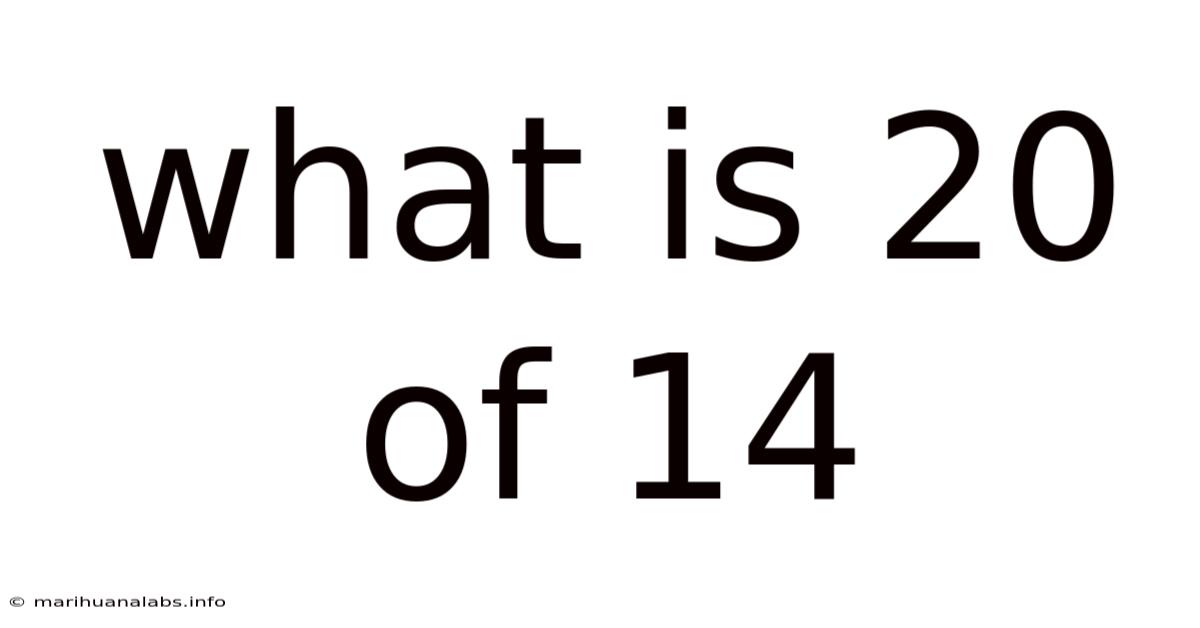
Table of Contents
What is 20 of 14? Understanding Fractions, Percentages, and Ratios
This seemingly simple question, "What is 20 of 14?", opens the door to a deeper understanding of fundamental mathematical concepts like fractions, percentages, and ratios. At first glance, it might seem illogical to take 20 of 14, as 20 is larger than 14. However, the phrasing hints at a proportional relationship, requiring us to explore different interpretations and solutions. This article will delve into these interpretations, providing a comprehensive explanation suitable for learners of all levels.
Understanding the Ambiguity: Different Interpretations
The phrase "20 of 14" is inherently ambiguous. It lacks the precision of mathematical notation. To solve this, we need to interpret what the question means to arrive at the correct answer. There are three primary interpretations:
-
20 as a Multiplier: This interpretation treats "of" as a multiplication operator. In this case, the question becomes 20 multiplied by 14, resulting in 280. This is a straightforward calculation but unlikely to be the intended meaning given the context.
-
20 as a Percentage: This is the most probable interpretation. The question could be asking "What is 20% of 14?". This involves calculating 20% of the value 14.
-
20 as a Ratio: This interpretation suggests a ratio of 20 to 14. We would then simplify or use this ratio in further calculations depending on the problem's context. This is less probable given the question's wording, but we will address it for completeness.
Interpretation 2: Calculating 20% of 14
This is the most likely and practical interpretation of the question. Let's break down how to calculate 20% of 14.
Method 1: Using Decimal Conversion
- Convert the percentage to a decimal: 20% is equivalent to 0.20 (or simply 0.2).
- Multiply the decimal by the number: 0.2 x 14 = 2.8
Therefore, 20% of 14 is 2.8.
Method 2: Using Fraction Conversion
- Convert the percentage to a fraction: 20% is equivalent to 20/100, which simplifies to 1/5.
- Multiply the fraction by the number: (1/5) x 14 = 14/5 = 2.8
Again, we arrive at the same answer: 2.8.
This method highlights the close relationship between percentages and fractions. Both represent parts of a whole.
Interpretation 3: Exploring the Ratio of 20 to 14
While less likely given the phrasing, the question could be interpreted as a ratio problem. The ratio of 20 to 14 is written as 20:14. This ratio can be simplified by finding the greatest common divisor (GCD) of 20 and 14, which is 2.
- Simplify the ratio: Dividing both numbers by 2, we get the simplified ratio 10:7.
This simplified ratio represents the same proportional relationship as 20:14. The usefulness of this ratio depends entirely on the context of a broader problem. For instance, if we had a recipe requiring 20 units of ingredient A and 14 units of ingredient B, the simplified ratio 10:7 would represent the same proportions using fewer units.
Expanding on Percentages: A Deeper Dive
Understanding percentages is crucial in numerous real-world applications. Here's a more in-depth look at the concept:
-
Percentages as Parts of a Whole: Percentages represent parts of a whole, where the whole is always considered 100%. For example, 50% means 50 out of 100, or half.
-
Calculating Percentages: The general formula for calculating a percentage of a number is: (Percentage/100) * Number.
-
Applications of Percentages: Percentages are used extensively in various fields, including:
- Finance: Calculating interest rates, discounts, taxes, and profits.
- Statistics: Representing data in charts and graphs.
- Science: Expressing concentrations of solutions and experimental results.
- Everyday Life: Understanding sales, tips, and proportions in recipes.
Expanding on Fractions: A Deeper Dive
Fractions, like percentages, represent parts of a whole. They are expressed as a ratio of two numbers: the numerator (top number) and the denominator (bottom number). Here are some key aspects of fractions:
-
Understanding Numerator and Denominator: The numerator indicates the number of parts considered, and the denominator indicates the total number of equal parts.
-
Types of Fractions:
- Proper Fractions: The numerator is smaller than the denominator (e.g., 1/2, 3/4).
- Improper Fractions: The numerator is equal to or larger than the denominator (e.g., 5/4, 7/3).
- Mixed Numbers: A combination of a whole number and a proper fraction (e.g., 1 1/2, 2 2/3).
-
Simplifying Fractions: Reducing a fraction to its simplest form involves dividing both the numerator and the denominator by their greatest common divisor.
-
Operations with Fractions: Addition, subtraction, multiplication, and division of fractions require specific rules and procedures.
Expanding on Ratios: A Deeper Dive
Ratios express the relative size of two or more values. They are used to compare quantities and can be written in different ways:
- Ratio Notation: a:b (e.g., 3:4)
- Fraction Notation: a/b (e.g., 3/4)
- Decimal Notation: a/b converted to a decimal (e.g., 0.75)
Key aspects of ratios include:
- Simplifying Ratios: Like fractions, ratios can be simplified by dividing all parts by their greatest common divisor.
- Equivalent Ratios: Ratios that represent the same proportional relationship (e.g., 1:2 is equivalent to 2:4, 3:6, etc.).
- Applications of Ratios: Ratios are used in various fields, including:
- Scaling: Enlarging or reducing drawings and models.
- Mixing: Determining the proportions of ingredients in recipes or solutions.
- Comparisons: Expressing the relative sizes of different quantities.
- Maps and Scales: Representing distances on maps.
Frequently Asked Questions (FAQ)
Q1: What is the difference between a ratio and a fraction?
While both ratios and fractions express a relationship between two numbers, fractions specifically represent parts of a whole, whereas ratios compare two or more quantities. A fraction always implies a part-to-whole relationship, while a ratio can compare any two quantities, not necessarily parts of the same whole.
Q2: Can I calculate 14% of 20?
Yes, absolutely. Using the percentage formula: (14/100) * 20 = 2.8.
Q3: How do I convert a fraction to a percentage?
To convert a fraction to a percentage, divide the numerator by the denominator and multiply the result by 100. For example, to convert 3/4 to a percentage, you would do (3/4) * 100 = 75%.
Q4: What if the question was "20 out of 14"?
The phrase "20 out of 14" implies an improper fraction (20/14), which simplifies to 10/7 or approximately 1.43. This represents more than one whole unit, unlike the percentage interpretation.
Conclusion
The seemingly simple question, "What is 20 of 14?", highlights the importance of clear communication and precise mathematical language. While the most probable answer, given the common usage of "of" to imply percentage, is 2.8 (20% of 14), understanding the context and exploring different interpretations (multiplication, percentage, and ratio) deepens our mathematical comprehension. Mastering the concepts of fractions, percentages, and ratios is essential for success in various academic and real-world scenarios. This article aimed not only to solve the initial question but also to equip you with the tools and knowledge to confidently tackle similar problems and further explore these fundamental mathematical ideas.
Latest Posts
Latest Posts
-
Sword And The Stone Squirrel
Sep 09, 2025
-
Transparent And Translucent And Opaque
Sep 09, 2025
-
How Many Sacraments Are There
Sep 09, 2025
-
Of Mice And Men Slim
Sep 09, 2025
-
Another Word For Team Player
Sep 09, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.