What Is 20 Of 12
marihuanalabs
Sep 15, 2025 · 6 min read
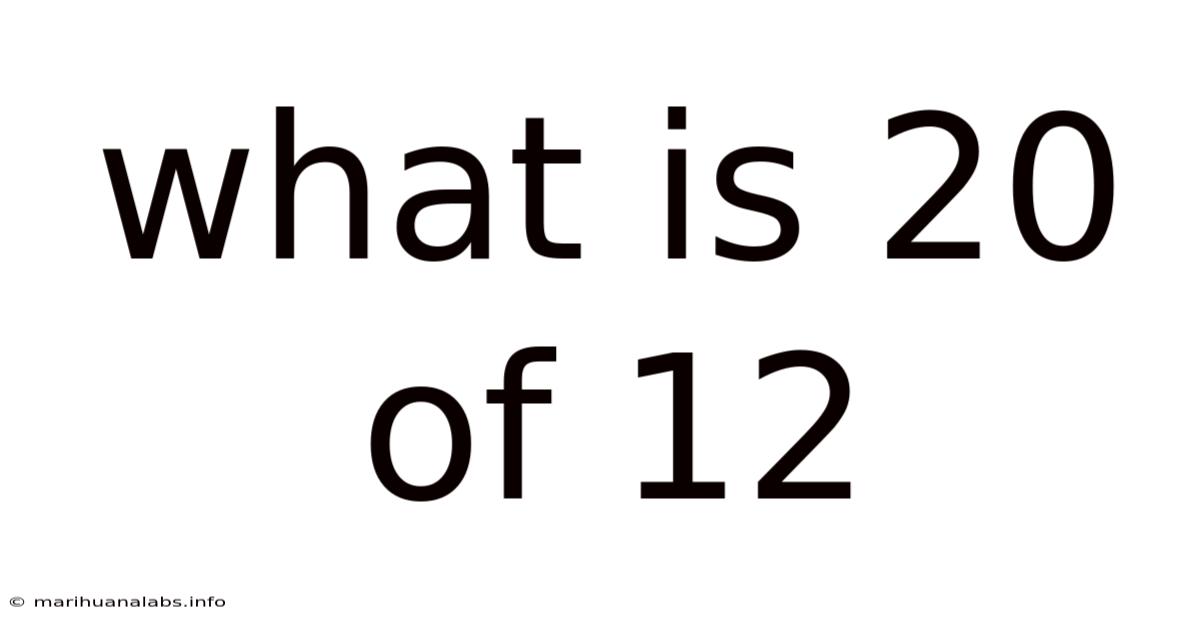
Table of Contents
What is 20 of 12? Understanding Fractions, Ratios, and Percentages
This seemingly simple question, "What is 20 of 12?", actually opens the door to a deeper understanding of fundamental mathematical concepts like fractions, ratios, and percentages. It's a question that can be interpreted in several ways, and understanding these interpretations is crucial for solving various real-world problems. This article will explore the different ways to interpret and solve this question, clarifying the underlying mathematical principles and providing practical examples.
Understanding the Ambiguity: The Importance of Context
The phrase "20 of 12" is inherently ambiguous. Without additional context, it's impossible to definitively determine the intended operation. Does it mean 20 out of 12? Does it refer to a ratio of 20 to 12? Or perhaps it's a percentage calculation, finding 20% of 12? Let's explore each possibility.
Interpretation 1: 20 out of 12 – An Improper Fraction
If "20 of 12" is interpreted as "20 out of 12," we are dealing with a fraction. This fraction, expressed as 20/12, is an improper fraction because the numerator (20) is larger than the denominator (12). Improper fractions represent a quantity greater than one whole.
Simplifying the Fraction: To simplify this fraction, we find the greatest common divisor (GCD) of 20 and 12, which is 4. Dividing both the numerator and the denominator by 4, we get:
20/12 = (20 ÷ 4) / (12 ÷ 4) = 5/3
This simplified fraction, 5/3, represents the same quantity as 20/12. It can also be expressed as a mixed number:
5/3 = 1 and 2/3
This means that "20 out of 12" represents one whole and two-thirds. In a practical context, this could represent having 20 items out of a possible 12, perhaps indicating an over-allocation or surplus. Imagine a situation where you expected 12 apples but received 20. The fraction 5/3 represents the excess apples relative to the expectation.
Interpretation 2: The Ratio of 20 to 12
Another interpretation is to consider "20 of 12" as a ratio. A ratio compares two quantities. In this case, the ratio is 20:12. Similar to fractions, ratios can be simplified by finding the GCD. The GCD of 20 and 12 is 4. Simplifying the ratio gives us:
20:12 = 5:3
This simplified ratio, 5:3, indicates that for every 5 units of one quantity, there are 3 units of another. This ratio could represent various real-world scenarios. For example, if a recipe calls for 12 parts flour and 20 parts sugar, the ratio of sugar to flour is 5:3. Or consider a business where for every 3 employees, there are 5 projects.
Interpretation 3: 20% of 12 – A Percentage Calculation
The phrase "20 of 12" could also be interpreted as "20% of 12". This implies a percentage calculation. To calculate 20% of 12, we convert the percentage to a decimal by dividing by 100:
20% = 20/100 = 0.2
Then, we multiply this decimal by 12:
0.2 * 12 = 2.4
Therefore, 20% of 12 is 2.4. This interpretation is relevant in various contexts like calculating discounts, tax rates, or proportions. Imagine a 20% discount on a $12 item; the discount amount would be $2.40.
Expanding the Understanding: Further Mathematical Explorations
The seemingly simple question, "What is 20 of 12?", has led us down a path exploring fractions, ratios, and percentages. These concepts are interconnected and fundamental to various mathematical applications. Let's delve deeper into these connections.
Fractions and Decimals: Interchangeability
Fractions and decimals are simply different ways of representing the same numerical value. We've already seen how an improper fraction, 20/12, can be simplified and expressed as a mixed number, 1 and 2/3. This fraction can also be converted to a decimal by performing the division:
20 ÷ 12 ≈ 1.666...
The repeating decimal 1.666... is another way to represent the value 5/3. Understanding this interchangeability is crucial for solving problems that involve both fractions and decimals.
Ratios and Proportions: Scaling Relationships
Ratios are fundamental to understanding proportions. A proportion is a statement that equates two ratios. For instance, if the ratio of boys to girls in a class is 5:3, and there are 15 girls, we can use a proportion to find the number of boys:
5/3 = x/15
Solving for x (the number of boys), we get x = 25. This demonstrates how ratios allow us to scale relationships and solve for unknown quantities.
Percentages and Their Applications
Percentages are simply fractions expressed as parts of 100. They are widely used to represent proportions, rates, and changes. Understanding percentage calculations is essential for various applications, including finance (interest rates, discounts), statistics (probability, data analysis), and everyday life (tips, sales tax).
Real-World Applications: Putting it All Together
Let's illustrate the practical applications of these concepts with a few examples:
-
Recipe Scaling: A recipe calls for 12 parts flour and 20 parts sugar. If you want to make a larger batch, and you have 30 parts of flour, you can use the ratio 12:20 (or 3:5) to calculate the required amount of sugar: 3/5 = 30/x; x = 50. You would need 50 parts of sugar.
-
Sales and Discounts: A store offers a 20% discount on an item priced at $12. The discount amount is 20% of $12, which is $2.40. The final price is $12 - $2.40 = $9.60.
-
Survey Results: A survey of 12 people shows that 20 prefer a particular brand. The fraction 20/12 (or 5/3) represents the proportion of people who prefer that brand.
Frequently Asked Questions (FAQ)
Q: What is the difference between a ratio and a fraction?
A: While both ratios and fractions compare quantities, ratios can compare different types of units (e.g., boys to girls), while fractions usually represent parts of a whole of the same unit. However, they are mathematically related and can often be expressed in similar ways.
Q: How do I convert a fraction to a percentage?
A: To convert a fraction to a percentage, divide the numerator by the denominator, then multiply the result by 100 and add the "%" sign. For example, 5/3 ≈ 1.67 * 100% = 167%.
Q: What if the question was "12 of 20"? How would that change the interpretation?
A: "12 of 20" would be interpreted similarly, but the resulting fraction (12/20) would simplify to 3/5, or 60% if interpreted as a percentage. The ratio would be 3:5.
Conclusion: The Power of Mathematical Understanding
The seemingly simple question "What is 20 of 12?" has revealed the richness and interconnectedness of fundamental mathematical concepts. Understanding fractions, ratios, and percentages is crucial for navigating various aspects of life, from everyday tasks to complex problem-solving in various fields. By clarifying the ambiguity and exploring different interpretations, we have highlighted the importance of precise language and contextual awareness in mathematics, emphasizing the practical application of these concepts in various scenarios. This understanding allows for more effective problem-solving and a deeper appreciation for the power of mathematical tools.
Latest Posts
Latest Posts
-
Thames River On Europe Map
Sep 15, 2025
-
Poem Out Of The Blue
Sep 15, 2025
-
Wiring Light Switch Uk Diagram
Sep 15, 2025
-
Corpus Christi Church Maiden Lane
Sep 15, 2025
-
Chronicles Of Narnia Tv Series
Sep 15, 2025
Related Post
Thank you for visiting our website which covers about What Is 20 Of 12 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.