What Is 15 Of 90
marihuanalabs
Sep 19, 2025 · 5 min read
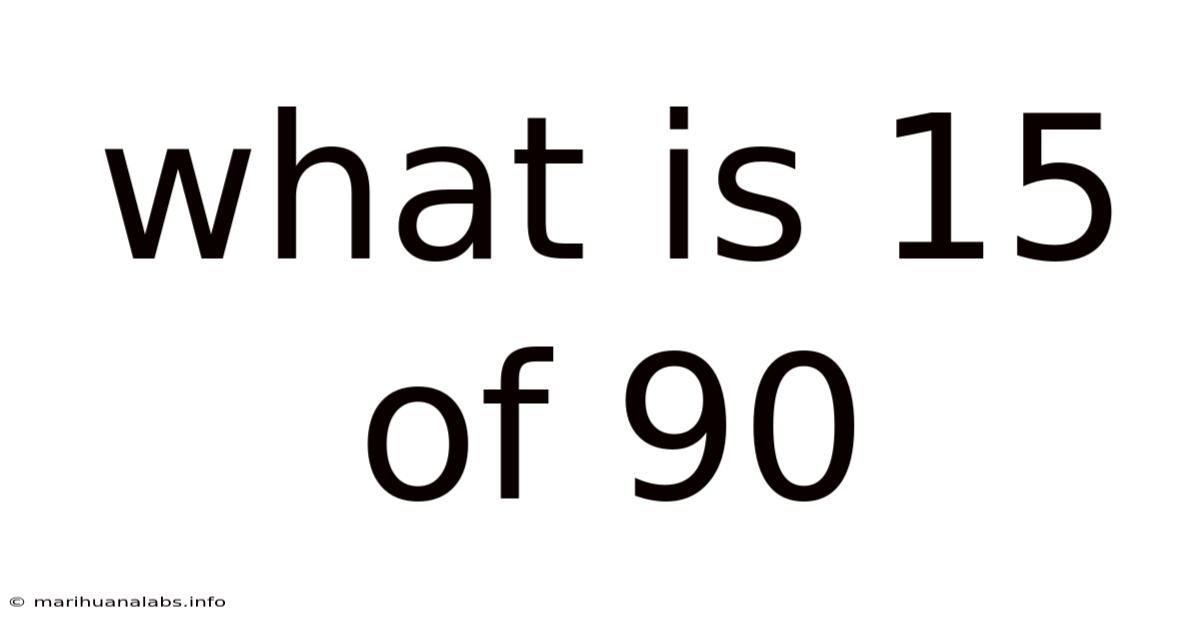
Table of Contents
What is 15/90? Understanding Fractions, Percentages, and Decimals
What is 15 out of 90? This seemingly simple question opens the door to a world of mathematical concepts, including fractions, percentages, and decimals. Understanding how to solve this, and similar problems, is crucial for everyday life, from calculating discounts to understanding statistics. This article will not only answer the question but also delve deeper into the underlying mathematical principles, providing you with a comprehensive understanding of how to approach such problems.
Introduction: Deconstructing the Fraction
The expression "15 out of 90" represents a fraction. In mathematics, a fraction expresses a part of a whole. In this case, 15 is the part and 90 is the whole. We can represent this as 15/90. This fraction can be simplified, converted to a decimal, and expressed as a percentage – all representing the same underlying value. We'll explore each of these representations in detail.
Simplifying the Fraction: Finding the Lowest Terms
Before converting 15/90 to a decimal or percentage, it's beneficial to simplify the fraction to its lowest terms. This makes the fraction easier to work with and provides a more concise representation of the value. To simplify a fraction, we find the greatest common divisor (GCD) of the numerator (15) and the denominator (90).
The GCD is the largest number that divides both the numerator and the denominator without leaving a remainder. Finding the GCD can be done through several methods, including listing factors or using the Euclidean algorithm. For 15 and 90, the GCD is 15.
Dividing both the numerator and the denominator by the GCD (15), we get:
15 ÷ 15 = 1 90 ÷ 15 = 6
Therefore, the simplified fraction is 1/6. This means that 15 out of 90 is equivalent to 1 out of 6.
Converting the Fraction to a Decimal: Division is Key
To convert a fraction to a decimal, we simply divide the numerator by the denominator. Using the simplified fraction 1/6:
1 ÷ 6 = 0.166666...
This decimal is a repeating decimal, meaning the digit 6 repeats infinitely. For practical purposes, we often round the decimal to a specific number of decimal places. Rounding to two decimal places, we get 0.17. This represents the decimal equivalent of 15/90.
Expressing the Fraction as a Percentage: Multiplying by 100
A percentage is a fraction expressed as a portion of 100. To convert a fraction or decimal to a percentage, we multiply by 100%. Using the decimal 0.166666... :
0.166666... × 100% ≈ 16.67%
Rounding to two decimal places, we find that 15 out of 90 is approximately 16.67%. This means that 15 represents approximately 16.67% of 90.
Understanding the Concepts: Fractions, Decimals, and Percentages
Let's reinforce the fundamental concepts involved:
-
Fractions: A fraction represents a part of a whole, expressed as a ratio of two numbers (numerator/denominator). For example, 15/90 represents 15 parts out of a total of 90 parts.
-
Decimals: Decimals represent numbers that are not whole numbers. They are based on the powers of 10, with the decimal point separating the whole number part from the fractional part. For instance, 0.17 represents 17 hundredths.
-
Percentages: Percentages express a fraction or decimal as a portion of 100. The symbol "%" represents "per hundred." 16.67% represents 16.67 parts out of 100 parts.
Real-World Applications: Putting it into Practice
The ability to convert between fractions, decimals, and percentages is valuable in many real-world scenarios:
-
Calculating Discounts: A store offers a 15% discount on an item priced at $90. Understanding percentages allows you to easily calculate the discount amount ($13.50) and the final price ($76.50).
-
Understanding Statistics: Statistics often use percentages and decimals to represent data. For example, understanding that 15 out of 90 students passed a test (16.67%) allows for a clear understanding of the test results.
-
Baking and Cooking: Recipes often use fractions to express ingredient quantities. Understanding fractions is essential for accurate measurements and consistent results.
-
Financial Calculations: Interest rates, loan payments, and investment returns are frequently expressed as percentages.
-
Data Analysis: In various fields, analyzing data often involves dealing with fractions, decimals and percentages to understand trends and relationships within data sets.
Frequently Asked Questions (FAQ)
-
Can I simplify 15/90 in a different way? Yes, you can simplify it step-by-step. You could initially divide both numerator and denominator by 5, resulting in 3/18, and then divide again by 3, resulting in 1/6. The final result will always be the same.
-
Why is it important to simplify fractions? Simplifying fractions makes them easier to work with and understand. A simplified fraction provides a more concise and efficient representation of the value.
-
What if I round the decimal to a different number of places? Rounding to different decimal places will affect the accuracy of the decimal representation. More decimal places give a more precise value. However, for most practical purposes, rounding to two decimal places is sufficient.
-
Can I directly convert 15/90 to a percentage without converting to a decimal first? Yes, you can. You can directly calculate (15/90) * 100% to get the percentage.
Conclusion: Mastering the Fundamentals
Understanding how to work with fractions, decimals, and percentages is a fundamental skill with far-reaching applications. This article has explored the process of determining what 15 out of 90 represents, showing how to simplify the fraction, convert it to a decimal and a percentage. Remember that mastering these basic mathematical concepts is key to success in various fields and everyday life. This seemingly simple question, "What is 15/90?", unlocks a broader understanding of mathematical principles and their practical significance. Continue practicing these conversions, and you'll find yourself confidently navigating numerical challenges in any context. The key lies in understanding the fundamental relationships between these three core mathematical representations.
Latest Posts
Latest Posts
-
What Does A Cardinal Do
Sep 19, 2025
-
How To Compute Flow Rate
Sep 19, 2025
-
Words That Rhyme With Understand
Sep 19, 2025
-
Passage From Book Crossword Clue
Sep 19, 2025
-
Book A Long Way Down
Sep 19, 2025
Related Post
Thank you for visiting our website which covers about What Is 15 Of 90 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.